斯坦福深度学习与自然语言处理高级的词向量表示
http://www.52nlp.cn/%E6%96%AF%E5%9D%A6%E7%A6%8F%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0%E4%B8%8E%E8%87%AA%E7%84%B6%E8%AF%AD%E8%A8%80%E5%A4%84%E7%90%86%E9%AB%98%E7%BA%A7%E7%9A%84%E8%AF%8D%E5%90%91%E9%87%8F%E8%A1%A8%E7%A4%BA
斯坦福大学深度学习与自然语言处理第三讲:高级的词向量表示
斯坦福大学在三月份开设了一门“深度学习与自然语言处理”的课程:CS224d: Deep Learning for Natural Language Processing,授课老师是青年才俊 Richard Socher,以下为相关的课程笔记。
第三讲:高级的词向量表示(Advanced word vector representations: language models, softmax, single layer networks)
推荐阅读材料:
- Paper1:[GloVe: Global Vectors for Word Representation]
- Paper2:[Improving Word Representations via Global Context and Multiple Word Prototypes]
- Notes:[Lecture Notes 2]
- 第三讲Slides [slides]
- 第三讲视频 [video]
以下是第三讲的相关笔记,主要参考自课程的slides,视频和其他相关资料。
回顾:简单的word2vec模型
- 代价函数J
- 其中的概率函数定义为:
- 我们主要从内部向量(internal vector)$v_{w_I}$导出梯度
计算所有的梯度
- 我们需要遍历每一个窗口内的中心向量(center vector)的梯度
- 我们同时需要每一个外部向量(external vectors)$v^'$的梯度
- 通常的话在每一个窗口内我们将更新计算所有用到的参数
- 例如在一个窗口长度为1的句子里:I like learning
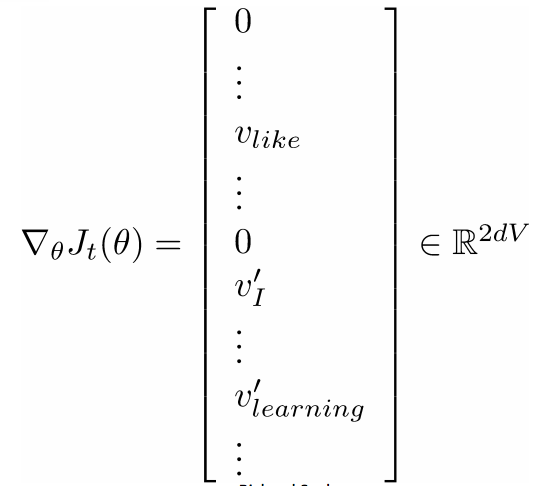
- 第一个窗口里计算的梯度包括:内部向量$v_{like}$, 外部向量$v^'_I$及$v^'_{learning}$
- 同理更新计算句子的下一个窗口里的参数
计算所有的向量梯度
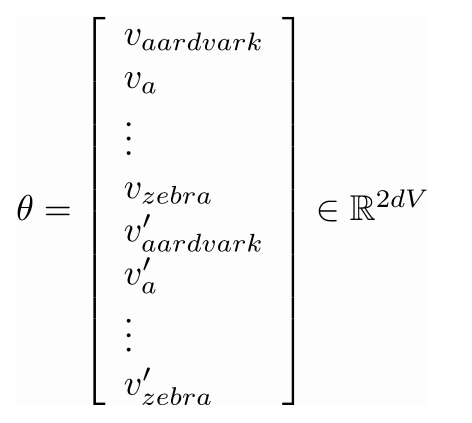
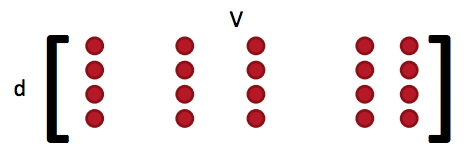
- 我们经常在一个模型里把所有的参数集合都定义在一个长的向量$\theta$里
- 在我们的例子里是一个d维度的向量及一个长度为V的词汇集:
梯度下降
- 要在整个训练集上最小化代价函数$J(\theta)$需要计算所有窗口里的参数梯度
- 对于参数向量$\theta$来说需要更新其中每一个元素:
- 这里$\alpha$是步长
- 从矩阵的角度来看参数更新:
梯度下降相关代码

随机梯度下降(SGD)
- 对于上述梯度下降的方法,训练集语料库有可能有400亿(40B)的token和窗口
- 一轮迭代更新需要等待很长的时间
- 对于非常多的神经网络节点来说这不是一个好方法
- 所以这里我们使用随机梯度下降(SGD):在每一个窗口计算完毕后更新所有的参数
词向量的随机梯度下降
- 但是在每一个窗口里,我们仅有2c-1个词,这样的话$\delta_{\theta}J_t(\theta)$非常稀疏
- 我们也许仅仅应该只更新那些确实存在的词向量
- 解决方案:或者保留词向量的哈稀或者更新词嵌入矩阵L和$L^'$的固定列
- 很重要的一点是如果你有上百万个词向量并且在做分布式训练的话就不需要发送大量的更新信息了
PSet1
- 归一化因子的计算代价很大
- 因此在PSet1你们将实现skip-gram模型
- 主要的思路:对一对实际的词对(一个中心词及一个窗口内的其他词)和一些随机的词对(一个中心词及一个随机词)训练二元逻辑回归模型
PSet1: The skip-gram model and negative sampling
- 来源论文:Distributed Representations of Words and Phrases and their Compositionality(Mikolov et al. 2013)
- 这里k是我们所使用的负例采样(negative sampling)的样本数
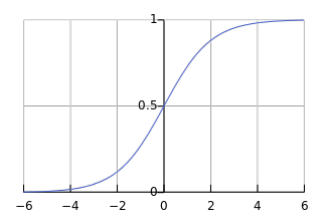
- Sigmoid函数:
- 所以我们最大化第一个log处两个词的共现概率
- 更进一步比较清晰的公式:
- 最大化在中心词周边真实词对的概率;最小化中心词周边随机词对的概率
- 这里unigram分布U(w)被赋予了3/4幂次方,这样可以保证一些出现比较少的词可以被尽可能多的抽样
What to do with the two sets of vectors?
- 我们从所有的向量v和$v^'$中得到了L和$L^'$
- 这两个都获得了相似的共现信息,如何有效的利用着两个向量集?一个简单有效的方法,对它们进行加和
- 在GloVe中对许多超参数进行了探究: Global Vectors for Word Representation (Pennington et al. (2014))
如何评测词向量
- 和一般的NLP评测任务相似:内部 vs 外部(Intrinsic vs extrinsic)
- 内部评测:
- 在一个特定的子任务中进行评测
- 计算迅速
- 有助于理解相关的系统
- 不太清楚是否有助于真实任务除非和实际的NLP任务的相关性已经建立起来
- 外部评测:
- 在一个真实任务中进行评测
- 需要花很长的实际来计算精度
- 不太清楚是否是这个子系统或者其他子系统引起的问题
- 如果用这个子系统替换原有的系统后获得精度提升-->有效(Winning!)
词向量的内部评测:
- 词向量类比:语法和语义
- 通过评测模型在一些语义或语法类比问题上的余弦相似度距离的表现来评测词向量
- 去除一些来自于搜索的输入词
- 问题:如果信息符合但不是线性的怎么办?
词向量的内部评测例一
- 词向量类比:以下语法和语义例子来源于:https://code.google.com/p/word2vec/source/browse/trunk/questions-words.txt
- 存在的问题:不同的城市可能存在相同的名字
词向量的内部评测例二
- 词向量类比:以下语法和语义例子来源于:https://code.google.com/p/word2vec/source/browse/trunk/questions-words.txt
词向量的内部评测例三
- 词向量类比:以下语法和语义例子来源于:https://code.google.com/p/word2vec/source/browse/trunk/questions-words.txt
词向量的内部评测例四
- 词向量类比:以下语法和语义例子来源于:https://code.google.com/p/word2vec/source/browse/trunk/questions-words.txt
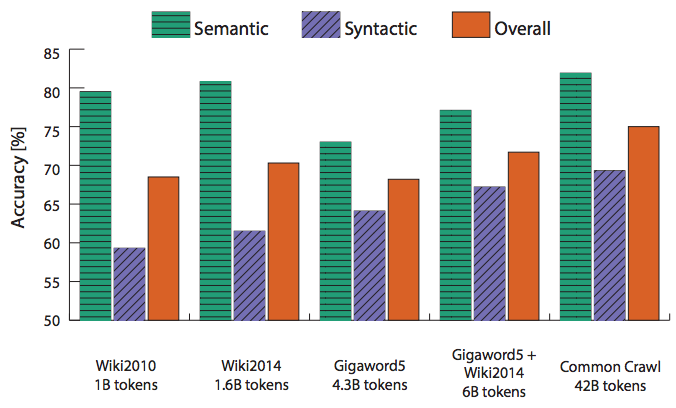
类比评测和超参数
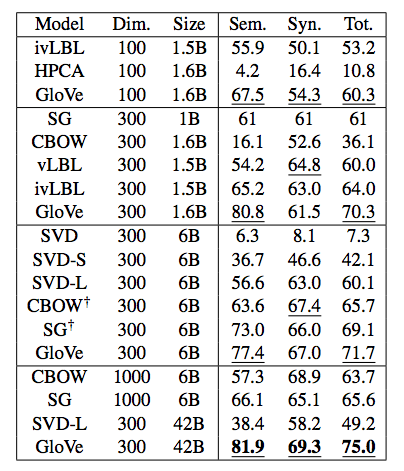
- 目前为止最细致的评测: GloVe 词向量
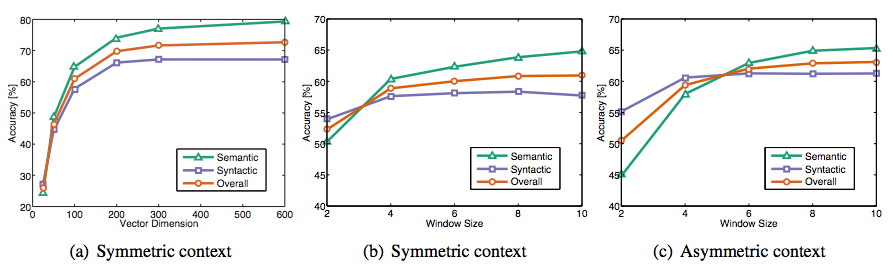
- 非对称上下文(仅有左侧的单词)并不是很好
- 最佳的向量维度:300左右,之后变化比较轻微
- 但是对于不同的“下游”任务来说最佳的维度也会不同
- 对于GloVe向量来说最佳的窗口长度是8
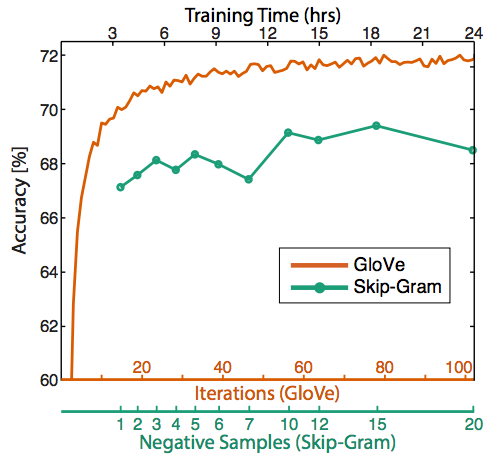
- 训练的时间约长是否有帮助:对于GloVe来说确实有助于
- 更多的数据是否有帮助?维基百科的数据比新闻数据更相关
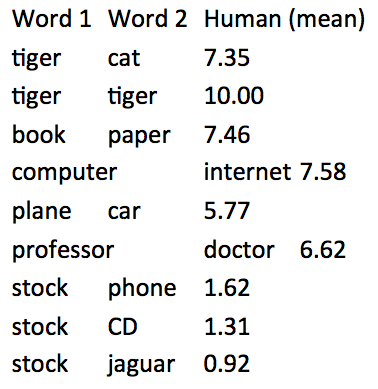
词向量的内部评价
- 评测任务:词向量距离以及和人工评价的相关性
- 评测集:WordSim353(http://www.cs.technion.ac.il/~gabr/resources/data/wordsim353/)
- 相关性评测结果:
如何应对歧义问题(But what about ambiguity?)
- 也许你寄希望于一个词向量能捕获所有的语义信息(例如run即是动车也是名词),但是这样的话词向量会被辣向两个方向
- 这篇论文对此有相应的描述:Improving Word Representations Via Global Context And Multiple Word Prototypes(Huang et al. 2012)
- 解决思路:对词窗口进行聚类,并对每个单词词保留聚类标签,例如$bank_1$, $bank_2$等
词向量的外部评价
简单的单个词的分类问题
- 从深度学习的词向量中最大的获益是什么?
- 有能力对单词进行精确的分类
- 国家类的单词可以聚和到一起-->因此可以通过词向量将地名类的单词区分出来
- 可以在其他的任务中将单词的任意信息融合进来
- 可以将情感分析(Sentiment)问题映射到单词分类中:在语料库中寻找最具代表性的正/负例单词
- 有能力对单词进行精确的分类
The Softmax
- 逻辑回归 = Softmax分类在给定词向量x的情况下获得y类的概率
The Softmax - 细节
- 术语:损失函数(Loss function) = 代价函数(Cost function) = 目标函数(Objective function)
- Softmax的损失(Loss): 交叉熵(Cross Entropy)
- 如何计算p(y|x): 取W的$y^'$行乘以含x的行
- 计算所有的$f_c$, c = 1, 2, ... , C
- 归一化计算Softmax函数的概率
Softmax和交叉熵误差
- 目标是最大化正确分类y的概率
- 因此,我们可以最小化改函数负的对数概率
- 因此,如果有多个类别我们可以在总的误差函数中叠加多个交叉熵误差
背景:交叉熵 & KL散度
- 假设分布是:p = [0,...,0,1,0,...0], 对应计算的概率分布是q,则交叉熵是:
- 因为p是one-hot的缘故,则上述公式剩余的则是真实类的负的对数概率
- 交叉熵可以写成熵和两个分布的KL散度之和
- 在我们的case里p是0(即使不是0也会因为它是固定的对梯度没有固定),最小化交叉熵等价于最小化KL散度
- KL散度并非是一个距离函数而是一个对于两个概率分布差异的非对称的度量
- 维基百科:KL散度是两个概率分布P和Q差别的非对称性的度量。 KL散度是用来 度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下,P表示数据的真实分布,Q表示数据的理论分布,模型分布,或P的近似分布。
简单的单个单词分类
- 例子:情感分析
- 两个选择:仅仅训练softmax权重W或者同时训练词向量
- 问题:训练词向量的优点和缺点是什么
- Pro: 更好的适应训练数据
- Con: 更差的泛化能力
继续“打怪升级”:窗口分类(Window classification)
- 单个的单词没有上下文信息
- 通过对窗口中的中心词进行分类同时考虑窗口中的上下文
- 可能性:Softmax 和 交叉熵误差 或者 最大边界损失(max-margin loss)
- 我们将在下一讲中探索这些问题(next class)




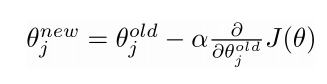
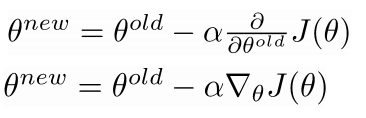

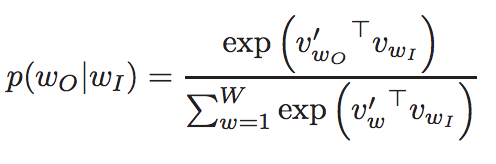

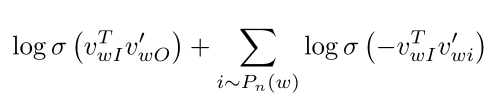
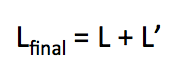









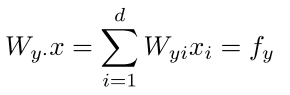
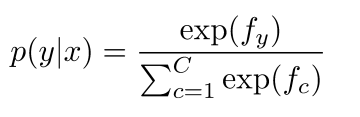

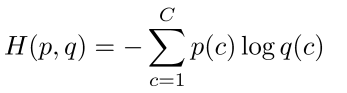
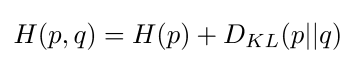


 浙公网安备 33010602011771号
浙公网安备 33010602011771号