FP-Growth算法
http://www.cnblogs.com/guozk/p/3316790.html
FP-Growth算法
FP-Growth(频繁模式增长)算法是韩家炜老师在2000年提出的关联分析算法，它采取如下分治策略：将提供频繁项集的数据库压缩到一棵频繁模式树（FP-Tree），但仍保留项集关联信息；该算法和Apriori算法最大的不同有两点：第一，不产生候选集，第二，只需要两次遍历数据库，大大提高了效率。
算法伪代码
算法：FP-增长。使用FP-树，通过模式段增长，挖掘频繁模式。
输入：事务数据库D；最小支持度阈值min_sup。
输出：频繁模式的完全集。
1． 按以下步骤构造FP-树：
(a) 扫描事务数据库D 一次。收集频繁项的集合F 和它们的支持度。对F 按支持度降序排
序，结果为频繁项表L。
(b) 创建FP-树的根结点，以“null”标记它。对于D 中每个事务Trans，执行：
选择 Trans 中的频繁项，并按L 中的次序排序。设排序后的频繁项表为[p | P]，其
中，p 是第一个元素，而P 是剩余元素的表。调用insert_tree([p | P], T)。该过程执行
情况如下。如果T 有子女N 使得N.item-name = p.item-name，则N 的计数增加1；否
则创建一个新结点N，将其计数设置为1，链接到它的父结点T，并且通过结点链结构
将其链接到具有相同item-name 的结点。如果P 非空，递归地调用insert_tree(P, N)。
2． FP-树的挖掘通过调用FP_growth(FP_tree, null)实现。该过程实现如下：
procedure FP_growth(Tree, α)
(1) if Tree 含单个路径P then
(2) for 路径 P 中结点的每个组合（记作β）
(3) 产生模式β ∪ α，其支持度support = β中结点的最小支持度；
(4) else for each a i 在 Tree 的头部 {
(5) 产生一个模式β = a i ∪ α，其支持度support = a i .support；
(6) 构造β的条件模式基，然后构造β的条件FP-树Treeβ；
(7) if Treeβ ≠ ∅ then
(8) 调用 FP_growth (Treeβ, β)；}
点Build后生成的头表和FP-Tree
点Step后生成再点Next会一次加入一个事务项进行生成FP-Tree
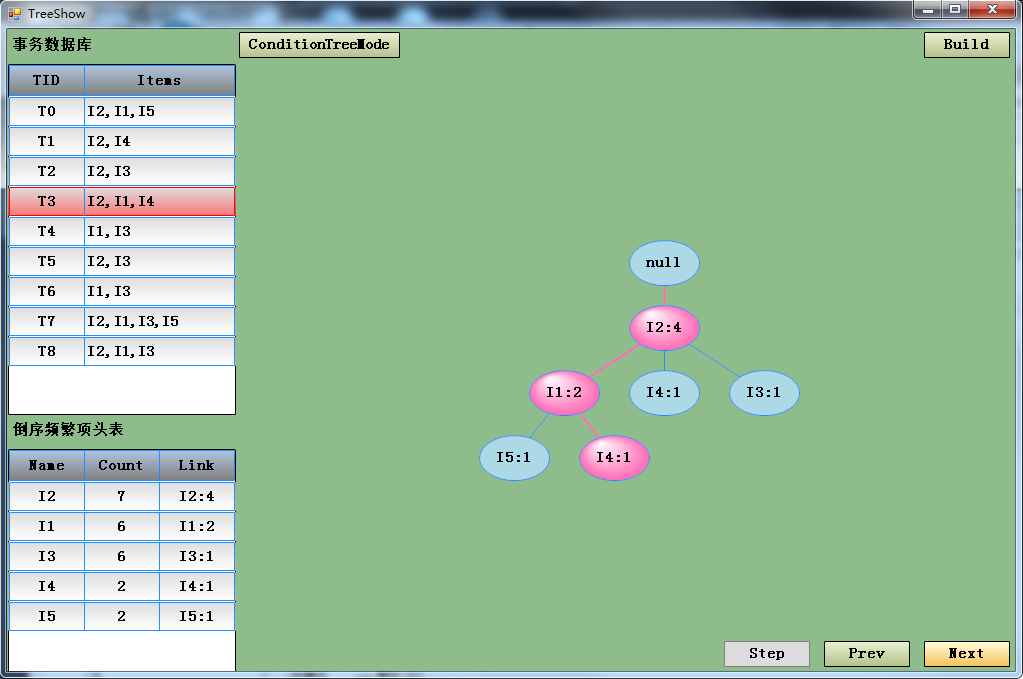
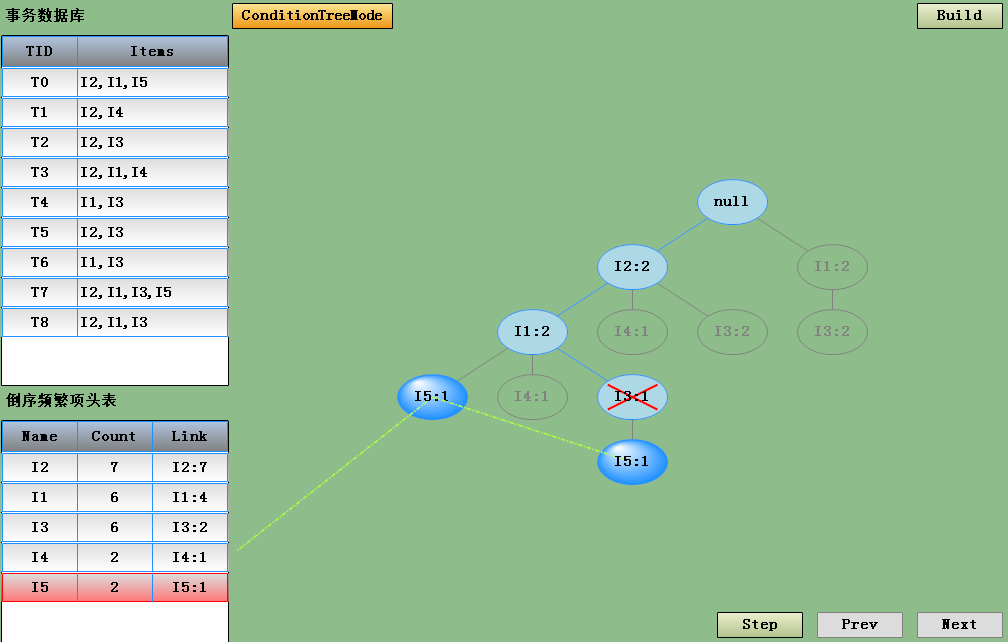
最后生成完了FP-Tree后点击ConditionTreeMode进入FP-Tree挖掘模式,显示当前头表中选中项的条件FP-Tree
