AtCoder 问题乱做集1

• AGC014D Black and White Tree

*2266

 

题目大意： 两个人在 $n$ 个节点的树上交替染色，先手染白色，后手染黑色。若染完之后有白点不与黑点相邻则先手胜，反之后手胜。求这棵树是先手必胜还是后手必胜。

$n\le 10^5$

 

显然如果一个节点的儿子中有超过一个叶子，那么先手只需要选择它就必胜了。

否则我们发现必然存在节点只有一个儿子且其为叶子，那么这两个节点见合（就是先手后手各走一个），没有意义，可以直接删去。

只要不停重复这个流程即可。注意最后如果只剩 $n$ 一个点也是先手胜（事实上，这也说明 $n$ 为奇数先手必胜）

实现的话，只要在 DFS 时对 $siz_u=2$ 的情况不上传就好。

 

inline void dfs(int u,int fa){
    siz[u]=1;
    for(int i=0;i<e[u].size();i++){
        int v=e[u][i];
        if(v==fa) continue;
        dfs(v,u);
        if(siz[v]>2) ok=1;
        else if(siz[v]<2) siz[u]+=siz[v];
    }
}
int main(){
    dfs(1,-1); ok|=(siz[1]!=2);
    puts(ok?"First":"Second");
    return 0;
}

 

• AGC030F Permutation and Minimum

*3474

题目大意：有一个 $2n$ 个数的排列 $A$，有些位置数字未确定。你可以将剩下的数字填入，然后得到长度为 $n$ 的序列 $B$ ： $B_i = \min\{A_{2 i - 1}, A_{2 i}\}$。求能得到的不同的 $B$ 的数量。

$1 \le n \le 300$

评分虚高，然而我自己做仍然没做出来 /kk

首先分好类：

• $A_{2i-1},A_{2i}$ 均未确定

 

• $A_{2i-1},A_{2i}$ 确定一个

 

• $A_{2i-1},A_{2i}$ 均确定

第三种情况显然可以直接丢掉。

由于 $B_i$ 在不断取 $\min$，我们不妨考虑从高往低填数，考虑每个数的配对情况，这样做就没有后效性。

转移就是说，如果 $x$ 为第一类数，那么他可以和第一类或第二类数匹配，也可以暂不匹配；如果 $x$ 为第二类数，那么他可以和第一类匹配，也可以暂不匹配。注意第二类数被第一类数匹配时是有顺序的，以及第一类数和第一类数匹配的系数没必要在 DP 时算，可以在算完答案后再乘上 $cnt!$。

 

#include<bits/stdc++.h>
using namespace std; 
int main(){
    n=read();
    for(int i=1;i<=n*2;i++) a[i]=read();
    for(int i=1;i<=n;i++)
        if((~a[i*2-1]) && (~a[i*2])) vis[a[i*2-1]]=vis[a[i*2]]=-1;
        else if(~a[i*2-1]) vis[a[i*2-1]]=1;
        else if(~a[i*2]) vis[a[i*2]]=1;
    f[0][0][0]=1; 
    for(int i=n*2;i;i--){
        if(vis[i]==-1) continue;
        ff^=1;
        for(int j=0;j<=n;j++)
            for(int k=0;k<=n;k++){
                f[ff][j][k]=0;
                if(vis[i]){
                    if(j) (f[ff][j][k]+=f[ff^1][j-1][k])%=mod;
                    (f[ff][j][k]+=f[ff^1][j][k+1])%=mod;
                }
                else{
                    if(k) (f[ff][j][k]+=f[ff^1][j][k-1])%=mod;
                    (f[ff][j][k]+=f[ff^1][j][k+1])%=mod;
                    (f[ff][j][k]+=1ll*(j+1)*f[ff^1][j+1][k]%mod)%=mod;
                }
            }
    }
    ans=f[ff][0][0];
    for(int i=1,j=0;i<=n;i++)
        if(a[i*2-1]==-1 && a[i*2]==-1) j++,ans=1ll*ans*j%mod;
    printf("%d\n",ans);
    return 0;
}

 

• AGC035B Even Degrees

*2039

题目大意：给一张无向简单连通图，判断能否给每一条边定向，使得每一个点出度为偶数。如果可以，请输出任意一种方案。

$2\le n \le 10^5,n-1 \le m \le 10^5$

人类智慧题。

首先 $m$ 为奇数必然无解。

然后就是人类智慧：随便拉出一棵生成树，非树边随便定向，树边根据儿子节点的情况定向。容易发现这样可以保证除了生成树根节点之外所有节点满足条件，又因为所有点出度之和为 $m$，是偶数，所以根节点也必然满足条件。时间复杂度 $O(n)$。

这个自己做要怎么才能想到啊 /ll

 

• AGC003E Sequential operations on Sequence

*2983

题目大意：一个初始长度为 $n$ 的数组，初始元素为 $1\sim n$，现在给 $Q$ 个操作，每次操作把数组长度变为 $q_i$，新增的数为上一个操作后的数组的重复。问 $Q$ 次操作后 $1\sim n$ 每个数出现了多少次。

$n,Q \le 10^5,q_i \le 10^{18}$

抽象思维题，或者说是 key observation problem。

首先如果 $i<j,q_i>q_j$，那么 $q_i$ 是没有意义的。用单调栈让 $q_i$ 单调上升。

然后考虑数组长度从 $q_i$ 到 $q_{i+1}$ 的过程，相当于先把当前数组复制 $\lfloor \frac{q_{i+1} } {q_i} \rfloor$ 次，再处理剩下的 $x=q_{i+1} \bmod q_i$ 个数。然后我们有一个重要的观察：对于一个 $j$ 满足 $q_j<d,q_{j+1}>d$，$q_j$ 与 $d$ 的关系与 $q_i$ 与 $q_{i+1}$ 的关系完全相同。每次二分找到 $j$ 后倒序递归处理，差分数组维护。时间复杂度 $O(n \log^2 n)$。

 

inline void solve(ll x,int i){
    if(stc[1]>x){ c[1]+=f[i]; c[x+1]-=f[i]; return; }
    int y=upper_bound(stc+1,stc+top+1,x)-stc-1;
    f[y]+=x/stc[y]*f[i];
    if(x%stc[y]) solve(x%stc[y],i);
}
int main(){
    f[top]=1; for(int i=top;i>=2;i--) f[i-1]+=stc[i]/stc[i-1]*f[i],solve(stc[i]%stc[i-1],i); 
    c[1]+=f[1]; c[stc[1]+1]-=f[1];
    for(int i=1;i<=n;i++) c[i]+=c[i-1],printf("%lld\n",c[i]);
    return 0;
}

 

• ABC152F Tree and Constraints

*1965

 

题目大意：给你一棵 $n$ 个节点的树，你要给这棵树黑白染色，并且符合 $m$ 条限制，每条限制给定 $u$ 和 $v$，需要满足 $u$ 到 $v$ 的路径上至少有一个黑色边，问有多少种染色方案。

$n\le50,m\le20$

 

看到 $m\le20$，考虑直接状压。

预处理一个状态数组 $sta$ 表示对于一条边，将其染为黑色能满足条件的限制状态。对于第 $i$ 个限制 $(u,v)$，我们直接把路径上所有边拉出来，并把 $i$ 并给这些边的状态。

然后你发现这个问题已经和树的形态无关了，直接设 $f_s$ 表示处理到当前边，已经满足的限制状态为 $s$ 的方案数。对于当前边 $i$ 而言，转移就是：

$f_{s \space \cup \space sta_i} = f_{s \space \cup \space sta_i}+ f_s$

直接转移即可，时间复杂度 $O(n \times 2^m)$。

 

inline void dfs3(int u){
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa[u]) continue;
        dfs3(v);
        for(int j=(1<<m)-1;~j;j--)
            f[sta[v]|j]+=f[j];
    }
}
int main(){
    n=read();
    for(int i=1;i<n;i++){
        int u=read(),v=read();
        add(u,v); add(v,u);
    }
    dfs1(1); dfs2(1,1);
    m=read();
    for(int i=1;i<=m;i++){
        int u=read(),v=read(),g=lca(u,v);
        while(u!=g) sta[u]|=1<<i-1,u=fa[u];
        while(v!=g) sta[v]|=1<<i-1,v=fa[v];
    }
    f[0]=1; dfs3(1); printf("%lld\n",f[(1<<m)-1]);
    return 0;
}

 

• ABC248G GCD cost on the tree

*2514

 

题目大意：给定一棵 $n$ 个节点的树，每个结点上有一个权值  $a_i$。对于每条至少包含两个点的链，它的贡献为链上点的数量(包括端点) $\times$ 链上所有权值的最大公约数。

求树上所有链的贡献之和。

$2\le n \le 10^5,1 \le a_i \le 10^5$

 

考虑枚举 GCD 的值为 $t$，求出每个 $t$ 对应的方案数 $f_t$。

直接求出有多少路径的 GCD 等于它不好求，我们考虑先求出满足 GCD 的值为 $t$ 的倍数的方案数 $g_t$，则 $f_t=g_t-\sum{f_{it}} (i>1)$。

对于 $g_t$，我们先把所有满足 $t \space | \space a_i$ 的 $i$ 拉出来建出一个森林，在每一棵树上做树形dp：

$cnt_i$ 表示 $i$ 的子树内，有一端点为 $i$ 的链的个数。

$len_i$ 表示 $i$ 的子树内，有一端点为 $i$ 的链的链长之和（准确的说应该是包括的点个数，没啥差别）。

$res_i$ 表示 $i$ 的子树内，经过 $i$ 的所有长度大于 $1$ 的链的长度之和。

那么 $g_t=\sum{res_i}$。

对于边 $(u,v)$，有转移：

$res_u=res_u+cnt_u \times len_v + cnt_v \times len_u$

前面的 $res_u$ 是因为 $v$ 子树内可以不选（但是 $u$ 必须选），后面是计算两棵子树合并，子树根处两条链拼起来的总长度。

$len_u=len_u+len_v+cnt_v$

$v$ 子树内的链会和 $u$ 接起来，长度加 $1$。

$cnt_u=cnt_u+cnt_v$

与 $len_u$ 同理。

然后就做完了，时间复杂度 $O(V \log V +n \sqrt V)$。

 

#include<bits/stdc++.h>
using namespace std;
inline void dfs(int u,int tt){
    cnt[u]=1; len[u]=1; res[u]=0; col[u]=0;
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(!col[v]) continue;
        dfs(v,tt);
        res[u]=(res[u]+(1ll*cnt[u]*len[v]%mod+1ll*cnt[v]*len[u]%mod)%mod)%mod;
        len[u]=(len[u]+len[v]+cnt[v])%mod;
        cnt[u]=cnt[u]+cnt[v];
    }
    (ans[tt]+=res[u])%=mod;
}
int main(){
    n=read();
    for(int i=1;i<=n;i++){
        int x=read(); m=max(m,x);
        for(int j=1;j*j<=x;j++)
            if(x%j==0){
                g[j].emplace_back(i);
                if(j*j<x) g[x/j].emplace_back(i);
            }
    }
    for(int i=1;i<n;i++){
        int u=read(),v=read();
        add(u,v); add(v,u);
    }
    for(int i=m;i;i--){
        if(g[i].empty()) continue;
        for(int j=0;j<g[i].size();j++) col[g[i][j]]=1;
        for(int j=0;j<g[i].size();j++) if(col[g[i][j]]) dfs(g[i][j],i);
        for(int j=i+i;j<=m;j+=i) (ans[i]+=mod-ans[j])%=mod;
    }
    for(int i=1;i<=m;i++) (sum+=1ll*ans[i]*i%mod)%=mod;
    printf("%d\n",sum);
    return 0;
}

 

 

• ARC083F Collecting Balls

*3541

题目大意：

$n\times n$ 的正方形上有 $2n$ 个小球，第 $i$ 个在 $(x_i,y_i)$。
有 $n$ 个 A 类机器人，第 $i$ 个在 $(0,i)$，有 $n$ 个 B 类机器人，第 $i$ 个在 $(i,0)$。
启动一个 A 类机器人后，它会向右走，将碰到的第一个球收集起来，并返回起点。启动一个 B 类机器人后，它会向上走，将碰到的第一个球收集起来，并返回起点。
只有上一个机器人返回起点后，下一个机器人才会被启动。每个机器人只能启动一次。
问有多少种启动机器人的顺序，能够收集完所有小球。

$n\le 10^5$

神中神题，想了半年点开题解发现思路连个边都没沾上 /ll

首先，我们把支配关系转化到图上，对于在 $(x,y)$ 的球，我们给第 $x$ 行与第 $y$ 列连无向边。

这样我们把问题转化为，我们需要给每条边选一个端点，让这个端点支配这条边。同时，同时如果边 $(u,v)$ 被 $u$ 支配，那么对于所有 $d<v$，$(u,d)$ 必须在 $(u,v)$ 之前被 $d$ 支配。

那么首先，如果这个图不是基环树森林，答案一定为 $0$。

那么现在考虑那个支配顺序关系。如果我们先把每棵基环树支配好（显然有两种方式，即和环上的支配顺序有关），然后把那个支配关系连上边，那么这又会变成一个森林。

然后答案就是这个森林的拓扑序数量，即 $\frac{2n!}{\prod{siz_i} }$。证明就是因为对于 $i$ 而言，有 $siz_i-1$ 个点不能在它前面，那么合法方案就要乘一个 $\frac{1}{siz_i}$ 的系数。

当然直接枚举定向关系再把每种情况的答案加起来复杂度就上天了，这里我们考虑加法原理的本质，即每棵基环树有两种定向方式，设其算出来的系数为 $A,B$，那么我们算完了其它部分的总系数 $T$ 后，合并起来的系数就应该是 $(A+B)T$。因此我们只需要对每棵基环树计算这个系数即可。

精细实现可做到 $O(n)$，反正我写的挺难受，可以看看完整代码感受下（bushi）。

 

#include<bits/stdc++.h>
using namespace std;
const int N=200005;
const int mod=1000000007;
inline int read(){
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return x*f;
}
int n,fac[N],inv[N],ans;
int dfn[N],low[N],idx,bri[N<<1],col[N],tr,ecnt; vector<int>g[N];
int cnt,vis[N],b[N],circnt,iscir[N],ctr[N],cir[N],deg[N],siz[N];
struct Edge{
    int to,nxt;
}e[N<<1],c[N];
int heade[N],tote,headc[N],totc;
inline void adde(int u,int v){
    e[++tote]={v,heade[u]};
    heade[u]=tote;
}
inline void addc(int u,int v){
    c[++totc]={v,headc[u]};
    headc[u]=totc;
}
inline void tarjan(int u,int fa){
    dfn[u]=low[u]=(++idx);
    for(int i=heade[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(!dfn[v]){
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>dfn[u]) bri[i]=bri[i^1]=1;
        }
        else if(v!=fa) low[u]=min(low[u],dfn[v]);
    }
}
inline void dfs1(int u,int fa){
    col[u]=tr; g[tr].emplace_back(u);
    for(int i=heade[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa || bri[i]) continue;
        if(col[v]){ ecnt++; continue; }
        dfs1(v,u);
    }
}
inline void dfs2(int u){
    vis[u]=1; b[++cnt]=u;
    for(int i=heade[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(vis[v]) continue;
        dfs2(v);
    }
}
inline void dfs3(int u,int fa){
    for(int i=heade[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(iscir[v] || v==fa) continue;
        ctr[v]=u; dfs3(v,u);
    }
}
inline void dfs4(int u,int fa){
    for(int i=heade[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v>=ctr[u]) continue;
        addc(u,v); deg[v]++;
    }
    for(int i=heade[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa || iscir[v]) continue;
        dfs4(v,u);
    }
}
inline int dfs5(int u,int fa){
    siz[u]=1; int res=1;
    for(int i=headc[u];i;i=c[i].nxt){
        int v=c[i].to;
        if(v==fa) continue;
        res=1ll*res*dfs5(v,u)%mod;
        siz[u]+=siz[v];
    }
    res=1ll*res*inv[siz[u]]%mod;
    return res;
}
inline int calc(){
    for(int i=1;i<=circnt;i++) dfs4(cir[i],-1);
    int ret=1;
    for(int i=1;i<=cnt;i++)
        if(!deg[b[i]]) ret=1ll*ret*dfs5(b[i],-1)%mod;
    return ret;
}
inline int solve(int rt){
    cnt=circnt=0; dfs2(rt);
    for(int i=1;i<=cnt;i++)
        if(iscir[b[i]]) dfs3(b[i],-1),cir[++circnt]=b[i];
    for(int i=1;i<=cnt;i++) headc[b[i]]=deg[b[i]]=0; totc=0;
    for(int i=1;i<circnt;i++)
        ctr[cir[i]]=cir[i+1];
    ctr[cir[circnt]]=cir[1];
    int ret=calc();
    for(int i=1;i<=cnt;i++) headc[b[i]]=deg[b[i]]=0; totc=0;
    for(int i=1;i<circnt;i++)
        ctr[cir[i+1]]=cir[i];
    ctr[cir[1]]=cir[circnt];
    (ret+=calc())%=mod;
    return ret;
}
int main(){
    n=read(); tote=1;
    for(int i=1;i<=n*2;i++){
        int u=read(),v=read();
        adde(u,v+n); adde(v+n,u);
    }
    fac[0]=fac[1]=inv[1]=1;
    for(int i=2;i<=n*2;i++) fac[i]=1ll*fac[i-1]*i%mod,inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
    for(int i=1;i<=n*2;i++) if(!dfn[i]) tarjan(i,-1);
    for(int i=1;i<=n*2;i++)
        if(!col[i]){
            tr++; ecnt=0;
            dfs1(i,-1);
            if(ecnt>2) return puts("0"),0;
        }
    for(int i=1;i<=tr;i++){
        if(g[i].size()==1) continue;
        for(int j=0;j<g[i].size();j++)
            iscir[g[i][j]]=1;
    }
    ans=1;
    for(int i=1;i<=n*2;i++)
        if(!vis[i]) ans=1ll*ans*solve(i)%mod;
    ans=1ll*ans*fac[n*2]%mod;
    printf("%d\n",ans);
    return 0;
}

 

• ABC259F Select Edges

*1961

题目大意：给定一棵 $n$ 个节点的树，每条边有一个权值 $w_i$。要求选择一些边，使得每个节点 $i$ 相邻的边中被选中的不超过 $d_i$ 条，请求出最大边权和。
$n\le 3\times 10^5,|a_i| \le 10^9$

这个都没独立做出来 /qd

考虑 DP。设 $f_{u,0/1}$ 表示 $u$ 向/不向父亲节点连边时，在子树内得到的最优值（其实就是 $f_{u,0}$ 在 $u$ 这里能多连一个儿子），用堆随便转移一下就好，时间复杂度 $O(n \log n)$。

 

• AGC032D Rotation Sort

*2602

 

题目大意：给定一个长度为 $n$ 的排列 $a$， 你可以花费 $A$ 使一个区间最左边的数跑到最右边， 或者花费 $B$ 的代价使最右边到最左边， 求把整个序列变成升序的最少花费。

$n\le5000,1\le A,B \le 10^9$

 

严重虚高，这个D比某些场次的AB简单的多...

考虑这个操作的本质，就是把一个数字往后插入，耗费 $A$ 的代价；把一个数字往前插入，耗费 $B$ 的代价。

那显然一个数最多操作一次，不操作的部分一定单调递增，那我们直接 DP 那个不操作的部分就好了。

设 $f_{i,j}$ 表示当前处理到第 $i$ 个数，留下的最后一个数为 $j$ 的最小代价。

$f_{i,j}=\begin{cases}f_{i-1,j}+A&a_i>j\\f_{i-1,j}+B&a_i<j\\f_{i-1,k} \space (k<a_i)&a_i=j\end{cases}$

直接转移即可，时间复杂度 $O(n^2)$。

用一个线段树做区间加区间求 $\min$ 还可以做到 $O(n \log n)$。

 

• AGC010C Cleaning

*2346

题目大意：一棵树，第 $1$ 个节点上有 $a_i$ 个石头，每次选择两个叶子节点（度数为 $1$ 的节点），将路径上经过的（包括起点终点）所有节点上都取走一个石头，如果路径上有一个点上没石头这个操作就不能进行，问能不能取完所有石头。
$2 \le n \le 10^5,0 \le a_i \le 10^9$

被薄纱，对着题解看了半年 /ll

考虑 $u$ 子树内来自不同儿子的路径：

• 如果在内部匹配，则路径条数减少 $2$，$a_u$ 减少 $1$。

 

• 如果向上匹配，则路径条数和 $a_u$ 都减少 $1$。

因此路径条数小于 $a_u$ 则无解。

如果重儿子（路径最多）的路径条数大于 $a_u$，则这个儿子传上来的路径无法匹配完，无解。

解方程 $cnt-2x=a_u-x$ 解得 $x=cnt-a_u$

向上传递即可，注意如果解出来 $x$ 不合法也是无解。如果最后做完之后根节点上还有没匹配的路径，也是无解。

注意要找到一个度数大于 $1$ 的点作为根，因为上面的决策都是对于非根节点的。

 

inline bool dfs(int u,int fa){
    if(deg[u]==1){ siz[u]=a[u]; return 1; }
    int sonmx=0;
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        if(!dfs(v,u)) return 0;
        siz[u]+=siz[v]; sonmx=max(sonmx,siz[v]);
    }
    if(siz[u]<a[u]) return 0;
    if(sonmx>a[u]) return 0;
    // a-x = sum-2x x=sum-a sum-2*sum+2a
    siz[u]=2*a[u]-siz[u];
    if(siz[u]<0) return 0;
    return 1;
}

 

• ARC121F Logical Operations on Tree

*2940

题目大意：给定一棵树，给每个点填 $0$ 或 $1$，给每条边填 AND 或 OR，在所有 $2^{2n-1}$ 种填法中，计数有多少种满足存在一种缩边的顺序，使得每次把一条边的两个端点缩成一个点，权为原端点与边的运算值，最终点的权为 $1$。
$2\le n\le 10^5$

感觉不难，有些虚高。自己瞎做一通搞出来了，比较感动。

注意到如果有叶子节点为 $1$ 且其到父亲的点标了 OR，那么其最终边权一定可以为 $1$。

然后就直接 DP 求边权为 $0$ 的方案数，用 $f_{u,0/1}$ 表示 $u$ 的子树内最后算出来权值为 $0/1$ 的方案数，转移的时候不讨论 $a_v=1 ,opt=\text{OR}$ 的情况即可。

 

inline void dfs(int u,int fa){
    int p0=1,q0=0,q1=1,son=0; // p0: u 这个点填 0 结果一定为 0 q0,q1：u 这个点填 1 当前结果为 0/1
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        dfs(v,u); son++;
        p0=1ll*p0*(f[v][0]*2%mod+f[v][1])%mod;
        q0=(1ll*q0*(f[v][0]*2%mod+f[v][1])%mod+1ll*q1*f[v][0]%mod)%mod;
        q1=1ll*q1*(f[v][0]+f[v][1])%mod;
    }
    f[u][0]=(p0+q0)%mod,f[u][1]=q1;
}

 

• AGC043D Merge Triplets

*2708

题目大意：

给定如下构造生成长度为 $3n$ 的排列 $P$ 的方法：

•   先生成一个长度为 $3n$ 的排列 $A$。然后将 $\forall k \in [0, N-1]$，$A_{3k+1},A_{3k+2},A_{3k+3}$ 分成一块。
•   有 $N$ 个指针，初始指向每个块的第一个数。
•   每次选择所有指针指向的数中最小的数删除，然后放到 $P$ 的末尾。之后指向被删除的数后移一个位置。若移出块了，则删除这个指针。

求一共能生成的 $P$ 有多少种。

$n\le2000$

神仙结论题，完全不会 /ll

大力找（he）规（ti）律（jie），发现生成排列合法的充要条件：

• 不存在长度大于 $3$ 的前缀 $\max$ 相同段，即不存在 $P_i>\max\{P_{i+1},P_{i+2},P_{i+3}\}$

 

• 长度为 $2$ 的前缀 $\max$ 相同段个数不大于长度为 $1$ 的前缀 $\max$ 相同段个数。

必要性很显然（但是我就是想不到结论 /ll），都是因为一个块里只有 $3$ 个数。充分性也很好证，你可以发现这样的排列一定可以直接构造出对应的原排列。

然后就是 DP 一下，设 $f_{i,j}$ 表示填到 $i$，有 $j$ 个长度为 $2$ 的段。转移的时候分别考虑填长度为 $1,2,3$ 的段：

$f_{i,j}=f_{i-1,j}+f_{i-2,j-1} \times (i-1) + f_{i-3,j-1} \times (i-2) \times (i-1)$

解释的话就是说段的第一个位置必须填当前最大值，剩下的位置可以随便选

直接转移即可。时间复杂度 $O(n^2)$。

 

• ARC101E Ribbons on Tree

*2913

题目大意：给定一个大小为 $n$ 的树，保证 $n$ 为偶数。

您需要给树上的点两两配对，并将配对点的简单路径覆盖，定义一个配对方案合法当且仅当所有边都被覆盖到（一次或多次），求合法方案数。

$n \le 5000$

感觉虚高，这个题没独立做出来，思维还差的多 /ll

先考虑一个 $O(n^3)$ 的简单做法：

设 $f_{u,i}$ 表示 $u$ 的子树内还有 $i$ 个点要向上匹配的方案数。我们发现如果 $(u,v)$ 这条边要被覆盖到，那么 $v$ 的子树内必然有点要向上匹配。

因此合并转移的时候枚举 $u$ 子树内的点数 $i$，$v$ 子树内的点数 $j$（注意 $j>1$），以及匹配的对数 $k$，有转移：

$newf_{u,i+j} = newf_{u,i+j} + f_{u,i} \times f_{v,j} \times {i \choose k} \times {j \choose k} \times k!$

答案即为 $f_{1,0}$。但是这样做系数很复杂，感觉完全没有优化的空间。

正难则反，考虑容斥求不合法方案。

对于不合法方案，我们可以看作断开一个边集 $S$，然后给每个联通块内两两配对，得到方案数 $T(S)$，对答案的贡献即为 $(-1)^k \times T(S)$。

容易发现的是，大小为 $2t$ 的联通块两两配对，方案数 $g(t)=\prod_{i=1}^{t} (2i-1)$

重新设状态 $f_{u,i}$ 表示在 $u$ 子树内，$u$ 所在联通块答案为 $i$ 的方案数。

考虑边的钦定情况，有转移方程：

$newf_{u,i} = newf_{u,i} + f_{u,i} \times f_{v,j} \times (-g(j))$ 钦定该边被断

$newf_{u,i+j} = newf_{u,i+j} + f_{u,i} \times f_{v,j}$ 该边没被断

答案为 $\sum_{i=1}^n f_{1,i} \times g(i)$。时间复杂度 $O(n^2)$。

 

inline void dfs(int u,int fa){
    siz[u]=1; f[u][1]=1;
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        dfs(v,u);
        for(int j=1;j<=siz[u];j++) ff[j]=f[u][j],f[u][j]=0;
        for(int j=1;j<=siz[u];j++)
            for(int k=1;k<=siz[v];k++){
                (f[u][j]+=mod-1ll*ff[j]*f[v][k]%mod*g[k]%mod)%=mod;
                (f[u][j+k]+=1ll*ff[j]*f[v][k]%mod)%=mod;
            }
        siz[u]+=siz[v];
    }
}

 

• ABC216G 01Sequence

  for(int i=1;i<=m;i++){
          int l=read(),r=read(),x=read(); x=r-l+1-x;
          // a[r]<=a[l-1]+x
          add(l-1,r,x);
      }
      for(int i=1;i<=n;i++){
          // a[i]<=a[i-1]+1 a[i-1]<=a[i]
          add(i-1,i,1); add(i,i-1,0);
      }
      dijkstra(0);
      for(int i=1;i<=n;i++) printf("%d%c",1-(dis[i]-dis[i-1]),i==n?'\n':

*1963

题目大意：构造一个长度为 $n$ 的 $01$ 序列，满足 $m$ 个限制 $(l_i,r_i,x_i)$：在 $[l_i,r_i]$ 这段区间内，序列上 $1$ 的个数不小于 $x_i$。你需要保证你的方案中包含 $1$ 的个数最小。

数据保证有解。

$1 \le n,m \le 2 \times 10^5$

简单差分约束，想到前缀和就会了，对前缀和列出不等式跑一下最短路即可。

注意 duliu 出题人卡 SPFA，所以必须确认你的连边方式是非负的，且能保证得到 $1$ 的个数最少。我的方法是维护 $0$ 意义下的前缀和求最短路。

 

for(int i=1;i<=m;i++){
    int l=read(),r=read(),x=read(); x=r-l+1-x;
    // a[r]<=a[l-1]+x
    add(l-1,r,x);
}
for(int i=1;i<=n;i++){
    // a[i]<=a[i-1]+1 a[i-1]<=a[i]
    add(i-1,i,1); add(i,i-1,0);
}
dijkstra(0);
for(int i=1;i<=n;i++) printf("%d%c",1-(dis[i]-dis[i-1]),i==n?'\n':' ');

 

• ABC221G Jumping sequence

*2914

 

题目大意：

有一个无限大的平面直角坐标系，初始时你在 $(0,0)$ 处。给你一个长度为 $n$ 的序列 $d$，你可以移动 $n$ 步，每一步可以选择向上下左右四个方向中的一个移动 $d_i$ 的距离。你想在 $n$ 步结束后位于 $(A,B)$ 位置，问是否存在这样的方案，如果存在需输出任意一种方案。

$n \le 2000,d_i \le 1800,|A|,|B| \le 3.6 \times 10^6$

 

纯纯的套路题。

将坐标轴旋转 $45^\circ$，$(A,B)$ 变化为 $(A-B,A+B)$。然后操作就相当于从 $(x,y)$ 走到 $(x\pm d_i,y\pm d_i)$，这样两维就独立了。

对于每一维我们可以用 bitset 背包解决，但是要输出方案，需要开 $n$ 个值域在 $-3.6 \times 10^6 \sim 3.6 \times 10^6$ 的 bitset，然后你发现它开不下。再改一下，发现第二维不开两维就不会爆，有点难受。

那咋办呢？我们注意到在随机生成的数据下，我们的第二位在背包过程中不会访问到比较大的负下标（就是当值减到比较小的时候，我们直接不管它了）。但是如果数据精心构造一下，让合法方案的减法全部堆到前面，你这样就出事了。

于是我把序列 shuffle 一下，这下你该卡不掉我了吧（

还有就是一个比较有趣的细节：在随机数据下，解可能会很多，因此你在输出方案时不能一直往一个方向跑，不然有可能会 RE（

时间复杂度 $O(\frac{n|A|}{w})$。

 

#include<bits/stdc++.h>
using namespace std;
const int N=2005;
const int V=3650001;
const char ch[5]={'L','D','U','R'};
inline int read(){
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return x*f;
}
int n,rA,rB,A,B,ans[N];
struct Opt{ int x,y; }d[N];
bitset<V>f[N]; mt19937 rnd(10086001);
inline void solve(int X,int op){
    int flag=0; if(X<0) X=-X,flag=op;
    if(X>=V){ puts("No"); exit(0); }
    f[0].reset(); f[0][50000]=1;
    for(int i=1;i<=n;i++)
        f[i] = (f[i-1]<<d[i].x) | (f[i-1]>>d[i].x);
    if(!f[n][50000+X]){ puts("No"); exit(0); }
    for(int i=n;i;i--){
        if(X<0){
            if(f[i-1][50000+X+d[i].x]) X+=d[i].x,ans[d[i].y]|=flag;
            else X-=d[i].x,ans[d[i].y]|=flag^op;
        }
        else{
            if(f[i-1][50000+X-d[i].x]) X-=d[i].x,ans[d[i].y]|=flag^op;
            else X+=d[i].x,ans[d[i].y]|=flag;
        }
    }
}
int main(){
    n=read(),rA=read(),rB=read(); A=rA-rB,B=rA+rB;
    for(int i=1;i<=n;i++) d[i].x=read(),d[i].y=i; shuffle(d+1,d+n+1,rnd);
    solve(A,1); solve(B,2);
    puts("Yes");
    for(int i=1;i<=n;i++) putchar(ch[ans[i]]);
    putchar('\n');
    return 0;
}

 

•  ABC240Ex Sequence of Substrings

*3184

题目大意：给定一个长度为 $n$ 的 $01$ 串，求最多可以选出多少互不相交的子串，满足这些子串按照原串中的顺序，字典序严格升序。

$n\le 25000$

 

虚高吧这玩意。

数据范围看上去就是根号老哥或者三只老哥的东西。

首先，我们选出来的子串，相邻的长度差一定不会大于 $1$。

于是我们容易发现直接过滤掉长度大于 $\sqrt{2n}$ 的子串对答案没有影响。

那么像 Trie 那样直接 dfs 一遍，把所有长度在 $\sqrt{2n}$ 之内的子串按字典序排好序，然后就是一个类似于最长上升子序列的问题，直接树状数组优化 dp 就好。时间复杂度 $O(n \sqrt{n} \log n)$。

 

#include<bits/stdc++.h>
using namespace std;
const int N=25005;
const int sq=231;
int n,m,a[N]; vector<int>o[2]; char str[N];
struct BIT{
    int c[N];
    #define lowbit(x) (x&(-x))
    inline void update(int x,int y){ while(x<=n) c[x]=max(c[x],y),x+=lowbit(x); }
    inline int query(int x){ int res=0; while(x) res=max(res,c[x]),x-=lowbit(x); return res; }
}T;
struct Str{ int l,r; }b[N*sq];
inline void solve(vector<int>e,int len){
    if(e.empty() || len*len>n*2) return;
    vector<int>v[2];
    for(int i=0;i<e.size();i++){
        b[++m]={e[i],e[i]+len-1};
        if(e[i]+len-1<n) v[a[e[i]+len]].emplace_back(e[i]);
    }
    for(int i=0;i<2;i++) solve(v[i],len+1);
}
int main(){
    scanf("%d%s",&n,str+1);
    for(int i=1;i<=n;i++) a[i]=str[i]^'0';
    for(int i=n;i;i--) o[a[i]].emplace_back(i);
    solve(o[0],1); solve(o[1],1);
    for(int i=1;i<=m;i++){
        int ri=T.query(b[i].l-1)+1;
        T.update(b[i].r,ri);
    }
    printf("%d\n",T.query(n));
    return 0;
}

 

• ABC155F Perils in Parallel

*2738

题目大意：数轴上有 $n$ 盏电灯，每盏电灯有位置和状态（ $0/1$）两个属性。有 $m$ 种操作，第 $i$ 种操作可以将数轴上 $[L_i,R_i]$ 范围内的电灯状态取反。试构造操作方案使所有电灯状态为 $0$。

$n \le 10^5,m \le 2 \times 10^5, pos_i,L_i,R_i \le 10^9$

 

强大题。

区间取反看上去好难受，要首先想到转化为异或差分。

然后每个操作可以看作连一条 $(l,r+1)$ 的边，要选出一些边让每个点的度数的奇偶性与异或差分相同。

然后我们发现如果操作出现环那和没操作没区别，于是直接拉一个生成森林，DFS 求解即可。

 

#include<bits/stdc++.h>
using namespace std;
const int N=100005;
inline int read(){
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return x*f;
}
int n,m,c[N],d[N],vis[N],cnt,ans[N];
struct Edge{
    int to,nxt,id;
}e[N<<2];
int head[N],tot;
inline void add(int u,int v,int i){
    e[++tot]={v,head[u],i};
    head[u]=tot;
}
struct BO_om{
    int x,y;
    bool operator < (const BO_om &a) const { return x<a.x; }
}a[N];
inline int dfs(int u){
    int ret=d[u]; vis[u]=1;
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(vis[v]) continue;
        if(dfs(v)) ret^=1,ans[++cnt]=e[i].id;
    }
    return ret;
}
int main(){
    n=read(),m=read();
    for(int i=1;i<=n;i++) a[i].x=read(),a[i].y=read();
    sort(a+1,a+n+1);
    for(int i=1;i<=n;i++) c[i]=a[i].x,d[i]=a[i].y^a[i-1].y;
    for(int i=1;i<=m;i++){
        int rl=read(),rr=read();
        int x=lower_bound(c+1,c+n+1,rl)-c,y=upper_bound(c+1,c+n+1,rr)-c;
        if(x==y) continue;
        add(x,y,i); add(y,x,i);
    }
    dfs(n+1); for(int i=1;i<=n;i++) if(!vis[i] && dfs(i)) return puts("-1"),0;
    sort(ans+1,ans+cnt+1); printf("%d\n",cnt); for(int i=1;i<=cnt;i++) printf("%d%c",ans[i],i==cnt?'\n':' ');
    return 0;
}

 

• ARC121E Directed Tree

*2645

题目大意：

给定一棵 $n$ 个点的有根树。

定义一个 $1\sim n$ 的排列 $a$ 是合法的，当且仅当对于任意 $i$，不存在 $a_i\to i$ 的，经过至少一条边的路径。

求合法排列数量。

$n \le 2000$

 

和 ARC101E 做法很像，但我还是没做出来...

那个条件相当于 $p_i$ 不是 $i$ 的祖先，于是考虑容斥，考虑这样的状态：设 $f_{u,i,j}$ 表示 $u$ 的子树内，有 $i$ 个点被我钦定选择当作祖先（即有后代连向它），然后这些关系连出来了 $j$ 条链。容易发现的是，如果最后整个图在钦定完后有 $k$ 条链，那么这个方案对答案就有 $k!$ 的贡献。所以最后答案就是 $\sum{f_{1,i,j} \times j!}$。

但是直接这样转移是 $O(n^3)$。类似于 ARC101E，将容斥的 $-1$ 系数放在转移里面，就能够删掉第二维了，时间复杂度 $O(n^2)$。

inline void dfs(int u,int fa){
    siz[u]=1; f[u][0]=1;
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;if(v==fa) continue;
        dfs(v,u);
        for(int j=0;j<=siz[u];j++) ff[j]=f[u][j],f[u][j]=0;
        for(int j=0;j<=siz[u];j++)
            for(int k=0;k<=siz[v];k++)
                (f[u][j+k]+=1ll*ff[j]*f[v][k]%mod)%=mod;
        siz[u]+=siz[v];
    }
    for(int i=siz[u];~i;i--){
        (f[u][i+1]+=f[u][i])%=mod;
        f[u][i]=-1ll*i*f[u][i]%mod;
        if(f[u][i]<0) f[u][i]+=mod;
    }
}

 

• ARC063E Integers on a Tree

*2198

题目大意：一颗点权树，相邻节点点权差绝对值为 $1$。 现在一些点点权已确定，试构造一种方案。

 $n\le 10^5$

 

做法1：树形 dp 计算出每个数字能处于的范围，配合奇偶性判定答案可行性。水平太低，没写对。

做法2：考虑直接贪心，每次选一个确定的最小值然后拓展就行了... 为啥我这都想不到啊 /ll

int main(){
    n=read();
    for(int i=1;i<n;i++){
        int u=read(),v=read();
        add(u,v); add(v,u);
    }
    for(int i=1;i<=n;i++) val[i]=-111111;
    m=read();
    for(int i=1;i<=m;i++){
        int x=read(); val[x]=read();
        c[val[x]].emplace_back(x); mx=max(mx,val[x]);
    }
    for(int i=0;i<=mx;i++)
        for(int j=0;j<c[i].size();j++){
            int u=c[i][j];
            for(int k=head[u];k;k=e[k].nxt){
                int v=e[k].to;
                if(val[v] == val[u]-1 || val[v] == val[u]+1) continue;
                if(val[v]>-111111) return puts("No"),0;
                val[v]=val[u]+1; c[val[v]].emplace_back(v); mx=max(mx,val[v]);
            }
        }
    puts("Yes"); for(int i=1;i<=n;i++) printf("%d\n",val[i]);
    return 0;
}

 

• ARC068F Solitaire

*3042

 题目大意：将 $1\sim n$ 顺序加入双端队列，再依次弹出，求有多少种弹出序列，使得 $1$ 是第 $k$ 个被删的。

$k \le n \le 2000$

 

怎么才能有思维啊 /kk

 

首先一定要找到正确的切入点：加入完的序列是单谷的，因此删除出来的东西应该可以看作 $1$ 或 $2$ 个下降序列，剩下的数则是谷左边或者右边的连续一段。

然而我想半个小时连这个都没想到 /qd

然后考虑 dp 计数这个东西。为避免两个当前删除序列的最小值是影响转移，不妨从大往小考虑是否删除一个数字，尝试设出这样的 dp 状态：设 $f_{i,j}$ 表示删了 $i$ 个数，最小值为 $j$ 的方案数。

令当前两个删除序列为 $A,B$，且 $mina=j,minb > j$。考虑新填进来一个数 $k$。

• 放到 $A$ 里 则有 $f_{i+1,k}=f_{i+1,k}+f_{i,j} (k<j)$
• 放到 $B$ 里 则 $k>j$ 且为未填进来的最大数字。 $f_{i+1,j}=f_{i+1,j}+f_{i,j}$

大概照着转移，前缀和优化即可，注意转移边界，注意 $k<n$ 时答案还有 $2^{n-k-1}$ 的系数，注意要特判 $k=1$。

（代码实现方式略有不同，但本质无差别）

for(int i=2;i<=n;i++) f[i]=1,g[i]=i-1;
for(int i=2;i<k;i++){
    for(int j=2;j<=n;j++)
        f[j]=(g[n]-g[j-(n-i+1>=j)]+mod)%mod;
    for(int j=2;j<=n;j++)
        g[j]=(g[j-1]+f[j])%mod;
}
ans=(k==1?1:g[n]);
for(int i=1;i<=n-k-1;i++) (ans*=2)%=mod;

 

• AGC012D Colorful Balls

*2760

题目大意：

$n$ 个球，每个都有颜色和重量两个属性。
对于两个同颜色的球，如果重量和在 $x$ 以内可以交换位置。
对于两个不同颜色的球，如果重量和在 $y$ 以内可以交换位置。
问可以得到的颜色序列的方案数。

$n \le 2 \times 10^5$

 

严重虚高。

考虑给能交换的球连边，容易发现联通块内部的点顺序可以自由排列。因此对于每个独立的联通块，答案就是 $\frac {\sum{cnt_i} } { \prod_{cnt_i!} }$，整张图的答案就是所有联通块的答案乘起来。

直接建图是 $O(n^2)$ 的，但我们对于每个点，只有与最小的同色/异色球连边是有意义的。那么复杂度就是 $O(n \log n)$（瓶颈在排序）

这里只放连边部分的实现。

for(t=2;a[t].col==a[1].col;t++);
fir[a[1].col]=1;
for(int i=2;i<=n;i++){
    if(!fir[a[i].col]) fir[a[i].col]=i;
    else if(a[i].w+a[fir[a[i].col]].w<=X) add(fir[a[i].col],i),add(i,fir[a[i].col]);
    if(a[1].col!=a[i].col){
        if(a[i].w+a[1].w<=Y)
            add(1,i),add(i,1);
    }
    else if(t<=n && a[i].w+a[t].w<=Y)
        add(t,i),add(i,t);
}

 

• AGC008F Black Radius

*3995

 题目大意：给出一棵有 $n$ 个结点的树 $T=\{V,E\}$ 和 $V$ 的一个子集 $U$。定义一个结点的集合 $S$ 合法当且仅当 $S$ 能表示为 $\left\{ y \ | \ y \in V, \, dis(x,y) \leq d \right\}$ 的形式，其中 $x \in U, 0 \le d < n$。求一共有多少个合法的集合。
$n\le 10^5$

子任务：$U=V$。

 

捏麻，羊了以后啥都干不动，这个题从羊之前整到羊之后 /fn

先考虑 Subtask 是什么。

注意接下来的内容不计算整个树的情况，这种情况单独记，因为去掉这种情况后没有顶到上界，会有很多优秀的性质。

我们首先寻找一种精妙的对 $S(x,d)$ 不重不漏地计数的方式：在 $d$ 最小的位置计数。对于一种方案，在 $d$ 最小时对应的 $x$ 必然只有一种，可以考虑反证。

然后我们发现对于每个 $x$，可取的 $d$ 是一个有上界的东西。

• 不覆盖全树

$d<mxdis(x)$

• 不存在 $f(y,d-1)=f(x)$

$d-2<secdis(x)$

理由可以自己画下，这个不是很难。于是换根 dp 即可，可以得到 Subtask 的分数。

 

// Subtask
inline void dfs1(int u,int fa){
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        dfs1(v,u);
        if(mx1[v]+1>mx1[u]) mx2[u]=mx1[u],mx1[u]=mx1[v]+1;
        else if(mx1[v]+1>mx2[u]) mx2[u]=mx1[v]+1;
    }
}
inline void dfs2(int u,int fa){
    // d < mx1 && d-2 < mx2
    ans+=min(mx1[u],mx2[u]+2);
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        int l=(mx1[u]==mx1[v]+1)?(mx2[u]+1):(mx1[u]+1);
        if(l>mx1[v]) mx2[v]=mx1[v],mx1[v]=l;
        else if(l>mx2[v]) mx2[v]=l;
        dfs2(v,u);
    }
}

 

• AGC030B Tree Burning

*2342

 

题目大意：一个周长为 $L$ 的圆，上面有 $L$ 个整点 $0,1,\cdots,L-1$。有 $n$ 个整点上有树，保证每个整点上最多有一棵树。现在你从 $0$ 点出发，每次选择走到顺时针或逆时针方向的第一棵树，然后将它点燃。问点燃 $n$ 棵树能走过的最长距离。

$n \le 2\times 10^5, L \le 10^9$

 

第一感就是说我顺逆时针交叉走会比较优，但是样例一似乎就把这个想法叉掉了。

但事实上我们稍加限制即可：在第一次改变方向之后，顺逆时针交叉走必然最优。证明可以考虑如果你走出了形如 $\text{LRR}$ 这样的情况，我必然可以通过调整使它更优（且终点一致），如 $\text{RLR}$。

然后就用一个前后缀和递推计算即可，计算时要注意到达最后一个位置之后不需要返回原点。

int main(){
    for(int i=1;i<=n;i++) pre[i]=pre[i-1]+a[i]*2;
    for(int i=n;i;i--) suf[i]=suf[i+1]+(L-a[i])*2;
    for(int i=1;i<=n;i++){
        int mid=(i+n)/2;
        ans=max(ans,pre[mid]-pre[i-1]+suf[mid+1]-((i+n&1)?L-a[mid+1]:a[mid]));
    }
    for(int i=n;i;i--){
        int mid=(1+i+1)/2;
        ans=max(ans,suf[mid]-suf[i+1]+pre[mid-1]-((1+i&1)?a[mid-1]:L-a[mid]));
    }
    return 0;
}

 

• CF17-Final H Poor Penguin

*3988

 

题目大意：

在遥远的南极洲, 有一片冰山。
这片冰山的状态可以用一个 $n×m$ 的 $01$ 矩阵表示, 其中 $0$ 代表该位置是一块浮冰，$1$ 代表该位置是一块冰山，矩形外的任何地方都是海洋。
我们称一块位于 $(x,y)$ 的浮冰是稳定的, 当且仅当满足下列条件的至少一个：

• $(x−1,y),(x+1,y)$ 均不为海洋。

• $(x,y−1),(x,y+1)$ 均不为海洋。

任意时刻，若一块浮冰是不稳定的，则其会变为海洋，可以发现，具体变化的顺序不会影响最终 的答案。
现在在 $(a,b)$ 的位置有一只企鹅， 保证这个位置是一块浮冰，随着气温升高，冰山在慢慢融化成 为浮冰，企鹅想知道，至少需要有多少个位置的冰山融化成为浮冰才能使得 $(a,b)$ 这个位置最终变为海洋?
$n,m \le 40$

这评分其实虚高了不少吧qwq，感觉整个题的思路都还算自然。

样例确实有非常强的启示作用。

首先我们不管这个神秘的数据范围，毛估估一下，海洋出现的过程显然是从四个角落往中间跑的。

那么我们看上去就有一个答案的上界：以 $(a,b)$ 为中心切出来的四块矩形（包括边界）的冰山数量。

事实上，不构造数据直接随机的话，绝大多数答案都是这个。在 AT 上，它也过掉了近 30 个点（即使它样例 2 都没过）

那我们考虑啥时候答案会更优，手玩一下样例 2，发现它从两个角出发，将整个矩形切开了：

 

 

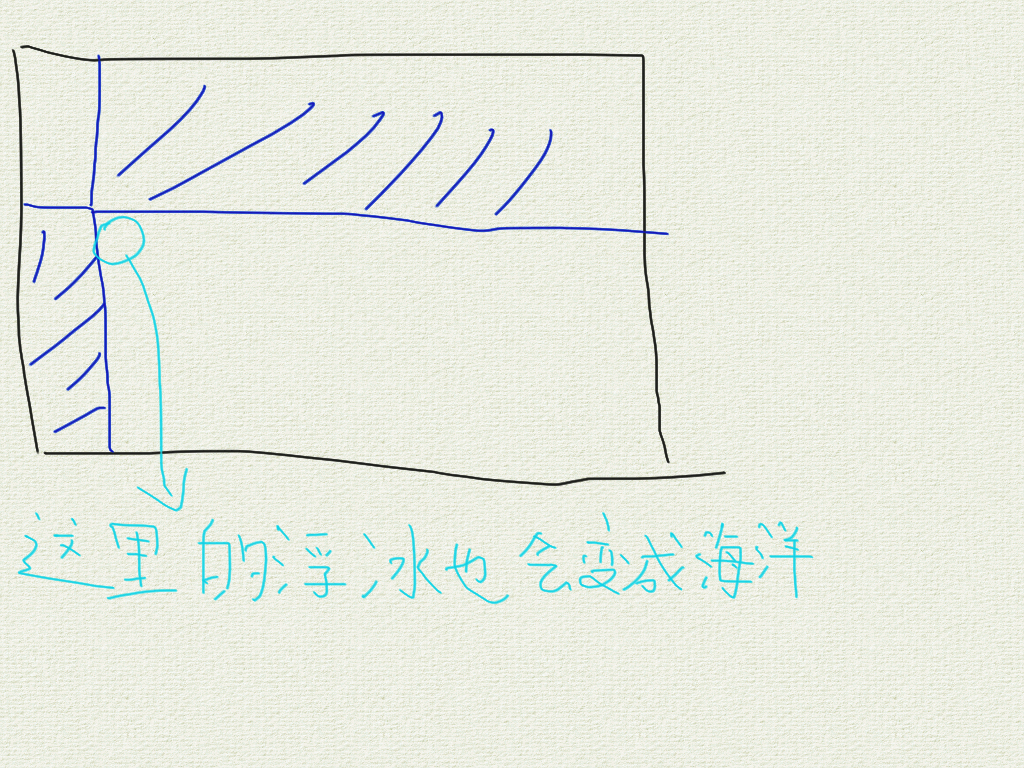
如果不考虑这种情况，上面的上界就是最优解。

然后你发现这相当于把大矩形挖掉两块，变成两个小矩形的子问题。

于是我们怎么暴力怎么来，直接设 $f_{i,j,k,l}$ 表示要把 $(i,j)$ 为左上角，$(k,l)$ 为右下角的矩形分出来需要的最小代价，转移时暴力枚举一个中间的切点，然后计算切掉两个角的贡献转移。最后统计答案直接枚举一个包含了 $(a,b)$ 的矩形，用那个上界算最后一部分的贡献即可。复杂度是优秀的 $O(n^6)$ /cf，反正写的不是太劣应该随便过。

 

#include<bits/stdc++.h>
#define y1 DitaMirika
using namespace std;
const int N=45;
inline int rd(){
    char ch=getchar();
    while(ch!='P' && ch!='+' && ch!='#') ch=getchar();
    return ch=='P'?2:ch=='#';
}
int main(){
    n=read(),m=read();
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            a[i][j]=rd();
            if(a[i][j]==2) X=i,Y=j,a[i][j]=0;
            c[i][j]=c[i-1][j]+c[i][j-1]-c[i-1][j-1]+a[i][j];
        }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            for(int k=n;k>=i;k--)
                for(int l=m;l>=j;l--)
                    f[i][j][k][l]=inf;
    f[1][1][n][m]=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            for(int k=n;k>=i;k--)
                for(int l=m;l>=j;l--)
                    for(int x=i;x<=k;x++)
                        for(int y=j;y<=l;y++){
                            f[i][j][x][y]=min(f[i][j][x][y],f[i][j][k][l]+query(i,y+1,x,l)+query(x+1,j,k,y));
                            f[i][y][x][l]=min(f[i][y][x][l],f[i][j][k][l]+query(i,j,x,y-1)+query(x+1,y,k,l));
                            f[x][j][k][y]=min(f[x][j][k][y],f[i][j][k][l]+query(i,j,x-1,y)+query(x,y+1,k,l));
                            f[x][y][k][l]=min(f[x][y][k][l],f[i][j][k][l]+query(i,y,x-1,l)+query(x,j,k,y-1));
                        }
    ans=inf;
    for(int i=1;i<=1;i++)
        for(int j=1;j<=1;j++)
            for(int k=n;k<=n;k++)
                for(int l=m;l<=m;l++)
                    ans=min(ans,f[i][j][k][l]+min(query(i,j,X,Y),min(query(i,Y,X,l),min(query(X,j,k,Y),query(X,Y,k,l)))));
    printf("%d\n",ans);
    return 0;
}

 

 

ARC114C Sequence Scores

*2056

 

简单题，但我做麻烦了。

先考虑一下我们的操作过程应该长什么样。

显然我们会按 $v$ 从小到大操作，这样一定是不劣的。

进一步的，我们对于 $x$ 的相邻出现位置，即 $a_i=a_j=x(i<j)$ 且 $\forall k \in [i+1,j-1] \space a_k \neq x$，如果 $\min\{a_i,\cdots,a_j\}<x$，则 $a_i,a_j$ 必须分两次操作赋值，对答案有 $1$ 的贡献。

记一个序列所有相邻出现位置统计得到的贡献为 $cnt_A$，所有数字的种类数为 $cnt_B$，那么答案即为 $cnt_A+cnt_B$。

$cnt_B$ 不难算，直接 dp（设 $f_{i,j}$ 表示序列长度为 $i$，有 $j$ 种不同数字的方案数） 或者容斥都不难做到 $O(nm)$。接下来考虑计数 $cnt_A$。

然后来设计一个暴力计数的方法：枚举左右端点 $L,R$ 以及值 $a_L=a_R=x$，我需要在中间放至少一个 $<x$ 的数以及若干 $>x$ 的数（注意不能 $=x$，因为我需要保证 $\forall k \in [L+1,R-1] \space a_k \neq x$），其他位置我们并不关心。容斥即可做到 $O(n^3m)$，推出来式子即：

$cnt_A=\sum_{L=1}^n \sum_{R=L+1}^n \sum_{x=1}^m \sum_{i=1}^{R-L-1} (-1)^{i-1} \times {R-L-1 \choose i} \times (x-1)^i \times (m-1)^{R-L-1-i} \times m^{n-(R-L+1)}$

其中 $i$ 为钦定 $<x$ 的数个数。

考虑优化这个式子，首先我们发现枚举 $L,R$ 的具体位置意义是不大的，在计算后面的式子时我们只关心 $R-L-1$ 的值。这样前面改成枚举 $len=R-L-1$，算出来的贡献再乘上 $n-len-1$（即对应左端点 $L$ 的取值个数），这样就是 $O(n^2m)$ 的了。

$\sum_{len=1}^{n-2} \sum_{i=1}^{len} \sum_{x=1}^m (-1)^{i-1} \times {len \choose i} \times (x-1)^i \times (m-1)^{len-i} \times m^{n-len-2}$

然后我们又发现式子里与 $x$ 唯一相关的项即为 $(x-1)^i$，那么对于相同的 $i$ 这个式子的总系数就是 $\sum_{x=1}^{m-1} x^i$，预处理一下即可去掉枚举 $x$ 的过程，总复杂度降至 $O(nm+n^2)$，可以通过本题。

我偷懒直接用了快速幂计算，复杂度为 $O(n^2 \log n)$，1995ms 极限通过。

n=read(),m=read(); Init(max(n,m)); f[0][0]=1;
for(int i=1;i<=n;i++)
    for(int j=1;j<=min(i,m);j++)
        f[i][j]=(1ll*f[i-1][j]*j+f[i-1][j-1])%mod;
for(int i=1;i<=min(n,m);i++) (ans+=1ll*C(m,i)%mod*fac[i]%mod*f[n][i]%mod*i%mod)%=mod;
for(int i=1;i<=n;i++)
    for(int val=2;val<=m;val++)
        (sumpw[i]+=qpow(val-1,i))%=mod;
for(int len=1;len<=n-2;len++){
    int ff=0;
    for(int i=1;i<=len;i++){
        int rr=1ll*C(len,i)*sumpw[i]%mod*qpow(m-1,len-i)%mod*qpow(m,n-2-len)%mod;
        if(i&1) (ff+=rr)%=mod;
        else (ff+=mod-rr)%=mod;
    }
    (ans+=1ll*(n-len-1)*ff%mod)%=mod;
}
printf("%d\n",ans);