生成树
瓶颈生成树
定义
无向图 \(G\) 的瓶颈生成树是这样的一个生成树,它的最大的边权值在 \(G\) 的所有生成树中最小
性质:
最小生成树是瓶颈生成树的充分不必要条件
最小瓶颈路
定义
无向图 \(G\) 中 \(x\) 到 \(y\) 的最小瓶颈路是这样的一类简单路径,满足这条路径上的最大的边权在所有 \(x\) 到 \(y\) 的简单路径中是最小的。
性质
根据最小生成树定义,x 到 y 的最小瓶颈路上的最大边权等于最小生成树上 x 到 y 路径上的最大边权。虽然最小生成树不唯一,但是每种最小生成树 x 到 y 路径的最大边权相同且为最小值。也就是说,每种最小生成树上的 x 到 y 的路径均为最小瓶颈路。
应用
由于最小瓶颈路不唯一,一般情况下会询问最小瓶颈路上的最大边权。
也就是说,我们需要求最小生成树链上的 max。
Kruskal 重构树
定义
按照 \(Kruskal\) 的构造方法,从小到大加入若干条边
首先新建 \(n\) 个集合,每个集合恰有一个节点,点权为 \(0\)
每一次加边会合并两个集合,我们可以新建一个点,点权为加入边的边权,同时将两个集合的根节点分别设为新建点的左儿子和右儿子。然后我们将两个集合和新建点合并成一个集合。将新建点设为根。
不难发现,在进行 \(n - 1\) 轮之后我们得到了一棵恰有 \(n\) 个叶子的二叉树,同时每个非叶子节点恰好有两个儿子。这棵树就叫 \(Kruskal\) 重构树。
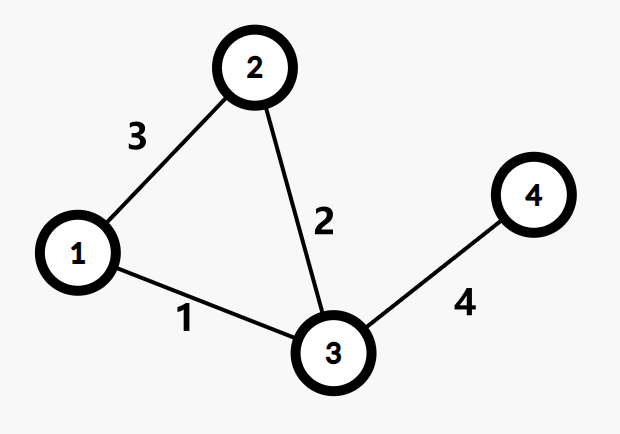
这个图的重构树为
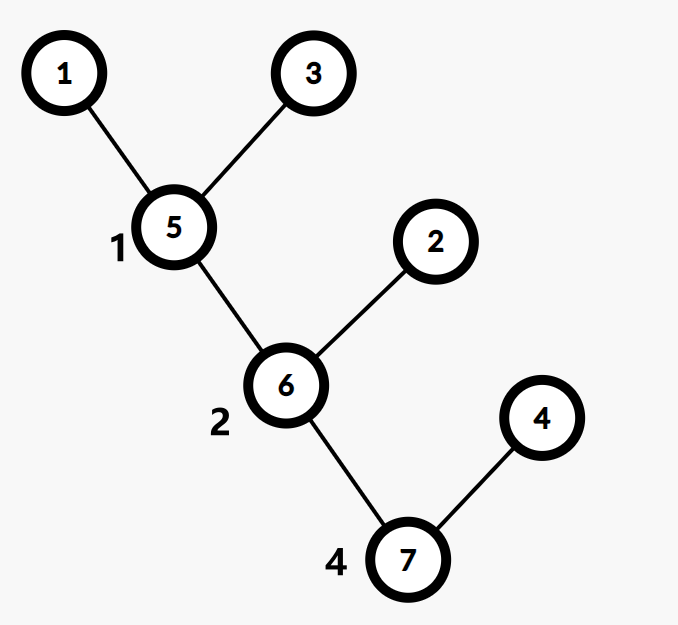
性质:
最小生成树上两个点之间的简单路径上边权最大值 \(= Kruskal\) 重构树上两点之间的 \(LCA\) 的权值。
也就是说,到点 \(x\) 的简单路径上边权最大值 \(\leq val\) 的所有点 \(y\) 均在 \(Kruskal\) 重构树上的某一棵子树内,且恰好为该子树的所有叶子节点。
在 \(Kruskal\) 重构树上找到 \(x\) 到根的路径上权值 \(\leq val\) 的最浅的节点。显然这就是所有满足条件的节点所在的子树的根节点。


