树形dp

树形dp

目录

• 树形dp
  • 简介
    • 树形dp
    • 状压dp
  • 树上背包
  • 栗题

简介

树形dp

在树上 \(dp\) ， 状态一般记录在节点上，转移一般是从儿子或者父亲继承，分析复杂度的时候通常考虑 \(LCA\)

状压dp

这一类题目的思路是最直接的——可以转换成 01 序列，然后就可以直接变成二进制形式压起来。 一般设计到与集合、子集相关的问题处理技巧

树上背包

有 \(N\) 件物品取出若干件放在空间为 \(V\) 的背包内，最后使得价值最大，但如果选了一个物品，必须要选择另一个物品

solution

\(f[x][v]\) \(x\) 的子树内花费 \(v\) 的容量所得到的最大价值

考虑合并子树背包

• 只有一个儿子的时候

直接把儿子转移上去

for (int i = 0; i <= V; i ++) f[x][i] = f[s[1]][i];
for (int i = V; i >= w[x]; i --)
	f[x][i] = max(f[x][i], f[x][i - w[x]] + v[x]); // 只有一个儿子 s1  

• 两个儿子？？

枚举每个儿子分了多少体积状物品，取 \(max\)

f[V], g[V], h[V]
for (int i = 0; i <= V; i ++) 
	for (int j = 0; j <= i; j ++)
		h[i] = max(h[i], f[j] + g[i - j]);

• 有多个儿子？？

先把第一个儿子合并上去，在与其他的儿子两两背包

for(int i = 0; i <= V; i++) f[x][i] = f[s[1]][i];//把第一个儿子合并上去 
for(int o = 2; o <= k; o++)//枚举其他儿子
   for(int i = 0; i <= V; i++)
   	  for(int j = 0; j <= i; j++)
   	  	    f[x][i] = max(f[x][i], f[s[o]][j] + f[x][i - j]);//父亲与儿子两两合并 
for(int i = V; i >= w[x]; i--)//考虑该节点选不选 
   f[x][i] = max(f[x][i], f[x][i - w[x]] + v[x]);

例题

有一棵节点为 \(n\) 的树，每个点都有一个权值 \(w_i\) 一条边两端至少选取一个点，问最大的收益，最后至多选取 \(k\) 个点，最大收益

\(n \leq 1000\)

solution

树上背包与没有上司的舞会的结合体？？

\(f[i][j][0/1]\) 表示 \(i\) 的子树内选了 \(j\) 个点的最大花费，\(i\) 点[选/不选]的最大花费

转移：

该节点不选：

\(f[x][i][0] = max(f[x][i][0], f[x][j][0] + f[s_1][i - k][1])\)

该节点选：

\(f[x][i][1] = max(f[x][i][1], f[i][j][1] + max(f[x][i - j][0] , f[x][i - j][1]))\)

时间复杂度 \(O(n^3)\)

code

// 不加 x 进入背包 
f[x][j][0]
for (int j = K; j >= 0; j --) 
	f[x][j][0] = f[s[1]][j][1];
for (int o = 2; o <= son; o ++)
	for (int i = 0; i <= K; i ++)
		for (int j = 0; j <= i; j ++)
			f[x][i][0] = max(f[x][i][0], f[x][j][0] + f[s[o]][i - j][1]);
//加入 x 进入背包 
f[x][j][1]
for (int j = K; j >= 0; j --)
	f[x][j][1] = max(f[s[1]][j][1], f[s[1]][j][0]);
for (int o = 2; o <= son; o ++)
	for (int i = 0; i <= K; i ++)
		for (int j = 0; j <= i; j ++)
			f[x][i][1] = max(f[x][i][1], f[x][j][1] + max(f[s[o]][i - j][1], f[s[o]][i - j][0]));			
for (int i = K; i >= 1; i --)
	f[x][i][1] = f[x][i - 1][1] + w[x];
f[x][0][1] = -INF;

考虑优化

考虑合并背包的时候，枚举两个分配的体积，其实两个背包的总和到不了 \(K\) ,最多只有两个背包的容量和，直接记录每个节点子树的大小 \(siz\) 合并的时候直接枚举两个节点子树大小就好了，但注意要倒着枚举 （\(01\) 背包）

时间复杂度 \(O(n^2)\)

code

void DP(int x)
{
	sz[x] = 0;
	for (int o = 1; o <= son; o ++) DP(s[o]);
for (int j = K; j >= 0; j --) 
	f[x][j][0] = f[s[1]][j][1];
for (int j = K; j >= 0; j --)
	f[x][j][1] = max(f[s[1]][j][1], f[s[1]][j][0]);
sz[x] = sz[s[1]];	
for (int o = 2; o <= son; o ++){
	for (int i = sz[x]; i >= 0; i --)
		for (int j = sz[s[o]]; j >= 0; j --){
			f[x][i + j][0] = max(f[x][i + j][0], f[x][i][0] + f[s[o]][j][1]);
			f[x][i + j][1] = max(f[x][i + j][1], f[x][i][1] + max(f[s[o]][j][1], f[s[o]][j][0]));
		}
//	sz[x] += sz[s[o]];
    for (int i = K; i >= 1; i --)
	f[x][i][1] = f[x][i - 1][1] + w[x];
    f[x][0][1] = -INF;
}

树的直径

• 两边 \(dfs\)
• 树上 \(dp\)

P3478 [POI2008]STA-Station

给出一棵 N 个点的树，找出一个点满足以这个点为根时，所有 点的深度之和最大。

\(N \leq 10^6\)

solution:

换个 \(dp\) ，先选取一个点作为根节点，求出所有点的子树大小和深度；然后进行换根；不难发现每个点的子树当根的时候都能答案都能根据它的父亲节点算出来；

\(f[v] = f[x] + n - 2 * siz[v];\)

栗题

[BZOJ3037创世纪]

有 \(n\) 个物品，每个物品都能限制另一种物品，现在选取一些物品放在背包里面，保证每个背包里面的物品都至少有一个背包外的物品限制它，求最多能放多少个背包

\(N \leq 10^6\)

solution

每个点出度都为 \(1\)， 考虑反向建边；

有这么一个性质：如果一个节点儿子都选了，则这个节点不能选，很显然

考虑从下到上贪心，显然每个叶子都不能选，然后根据那个性质从下到上把能选的点都选上；

环？？选一半的点就好了

\(dp\)

\(f[i][0/1]\) 表示至少要保留多少个节点，\(i\) 表示点的编号，\(0/1\) 表示当前的点是否保留

如果这个点选了，那么子节点至少不选一个点

如果这个点不选的话，子节点就都可以选

\(f[x][0] = \sum_{i = 1}^{siz[x]} max(f[s[i]][0], f[s[i]][1])\)

\(f[x][1] = （\sum_{j\neq i}max（ f[s[j]][0], f[s[j]][1])) + f[s[i]][0]+1\)

第二个式子枚举的话要 \(n^2\) ，其实发现括号里里面与上面的式子只是少了 \(j = i\) 这种情况

所以可以直接化简成

\(f[x][1] = f[x][0] - max(f[s[i]][0],f[s[i]][1]) + f[s[i]][0] + 1\)

环上：

删掉一条边，如果这个上点 \(x\) 不选的话那么另一个点 \(y\) 一定可以选 \(f[y][1] = f[y][0]\) \(y\) 这个点已经得到保证了，否则这条边没有用，删掉这条边，剩下的按照树的情况做就好了

Rainbow Roads

给出一棵树，每条边都有一种颜色，问从哪些点出发不存在一条连续有两条同色边的路径

\(n \leq 10^5\)

solution

暴力枚举每一个点进行 \(dfs\) （换根？？）

\(dp\)

假设节点 \(u\) 和节点 \(v\) 均与节点 \(w\) 相邻，且 \(e(w,u)\) 与 \(e(w,v)\) 颜色相同

分两种情况：

• \(u\)，\(v\) 均是 \(w\) 的子树，则这两个点的子树上所有的点包括这两个点不是合法的点。
• \(u\) 是 \(w\) 的父节点，\(v\) 是 \(w\) 的子节点，则 \(u\) 的外子树和 \(u\) 的内子树除 \(w\) 部分外的节点都是不合法的节点

然后用 \(dfs\) 打标记就好了

Hamiltonian Spanning Tree

题目大意：

有一个 \(n\) 个点的完全图， 这个完全图中每条边的边权都为 y，从中选了一个生成树，并把树边边权都改为了 \(x\)，求一条最短路径使得每个点都只经过一次

\(n ≤ 2 × 10^5 , x, y ≤ 10^9\)

solution

• 如果 \(x\geq y\) ，肯定要尽可能的走 \(y\) 边，除了菊花图外，一定有一种方案只走 \(y\) 边

不是菊花图的话最短路径长就是：\((n - 1)*y\)

是菊花图的话最短路径长就是 \(x + (n - 2) * y\)

• 如果 \(x \leq y\)，就要尽可能选树边，并且选出来的边使得每个点的度数为 2

树形 \(dp\)

\(f[x][0/1/2]\) 当前节点 \(x\) 的度数为 \(0/1/2\) 最多有能有多少条边

转移：

\(v\) 为 \(x\) 的一个儿子

\(f[x][0] = f[x][0] + max(f[v][0], f[v][1], f[v][2])\)

\(f[x][1] = max(f[x][1] + max(f[v][0], f[v][1], f[v][2]), f[x][0] + max(f[v][0], f[v][1]) + 1)\)

\(f[x][2] = max(f[x][2] + max(f[v][0], f[v][1], f[v][2]), f[x][1] + max(f[v][1], f[v][0]) + 1)\)

• 当前点的度数为 0， 所以与子节点连接的边不选，直接转移过去就好了

• 当前点度数为 1，可以由原来度数为 \(1\) 的状态直接转移，或者由度数为 \(0\) 的状态与儿子连一条边转移

• 当前度数为2，可以由原来度数为 \(2\) 的状态直接转移，也可以由度数为 \(1\) 的状态加上一条边后转移；注意：不能由 \(f[x][0]\) 进行转移，因为与一个儿子连的边最多有一条，仅靠一个儿子转移不过去

\(temp = max(f[1][0], f[1][1], f[1][2])\)

\(ans = x*temp + y*((n - 1) - temp)\)

注意：

• 要开longlong
• 转移方程枚举方程的枚举顺序，要倒着枚举

/*
work by:Ariel_
*/
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#include <algorithm>
#define int long long
using namespace std;
const int N = 200001;
int read(){
    int x = 0,f = 1; char c = getchar();
    while(c < '0'||c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') {x = x*10 + c - '0'; c = getchar();}
    return x*f;
}
int n, x, y, f[N][3], outd[N], ans, flag;
struct edge{int v, nxt;}e[N << 1];
int cnt, head[N];
void add_edge(int u, int v){
   e[++cnt] = (edge){v, head[u]}; head[u] = cnt;
}
void dfs(int x, int fa){
	for(int i = head[x]; i; i = e[i].nxt){
		  int v = e[i].v;
		  if(v == fa) continue;
		  dfs(v, x);
          int t1 = max(f[v][0], f[v][1]), t2 = max(t1, f[v][2]);
		  f[x][2] = max(f[x][2] + t2, f[x][1] + t1 + 1);
		  f[x][1] = max(f[x][1] + t2, f[x][0] + t1 + 1);
		  f[x][0] += t2;
       }
}
signed main(){
   n = read(), x = read(), y = read();
   for (int i = 1, u, v; i < n; i++){
   	  u = read(), v = read();
	  add_edge(u, v), add_edge(v, u);
	  outd[u]++, outd[v]++;
   } 
   dfs(1, 0); 
   if(x <= y){
   	  int temp = max(f[1][0], max(f[1][1], f[1][2]));
	  printf("%lld", x * temp + y * (n - 1 - temp));
   }
   else{
   	  for(int i = 1; i <= n; i++)
   	  	   if(outd[i] == n - 1){
   	  	   	  flag = 1; break;
		    }
	  if(flag) printf("%lld", x + (n - 2) * y);
	  else printf("%lld", (n - 1) * y);
   }
   puts("");
   return 0;
}

treecnt

给定一棵 \(n\) 个节点的树，从 \(1\) 到 \(n\) 标号。选择 \(k\) 个点，你需要选择一些边使得这 \(k\) 个点通过选择的边联通，目标是使得选择的边数最少。 现需要计算对于所有选择 \(k\) 个点的情况最小选择边数的总和为多少

\(1 \leq k \leq n \leq 10^5\)

solution

考虑每个边对答案的贡献，发现只有虚树上的边才会被统计

虚树： 所有的关键点( \(k\) 个点)和它的 \(lca\) 组成的一棵树（就是去除树上没用的部分）

所以一条边如果有贡献的话，\(k\) 个点一定分布在这条边的左右两边

当这条边左边有 \(a\) 个点，右边有 \(n - a\) 个点，那么 \(k\) 个点在一侧的方案数 \(\tbinom{a}{k} + \tbinom{n - a}{k}\)

合法的方案数就是 \(\tbinom{n}{k} - \tbinom{a}{k} - \tbinom{n - a}{k}\)

黑暗料理（from:dxy）

\(n\) 个节点的树，有 \(m\) 个点是关键点，\(m\) 个关键点中随机选取 \(k\) 个点有物品，现可以从树上任何一个点出发，要得到所有的物品，要求走的路径最短，求期望走多长距离

也就是求出 \(\sum\)$ \tbinom{m}{k}$ 的所有情况下的最短路径 最后除以 \(\tbinom{m}{k}\)

答案对 998244353 取模

\(n\leq10\) ，\(1 \leq k \leq m \leq 500\)

solution

very very good 的题目 /se

根据上一个题的思路，取出那 \(m\) 个关键点，建个虚树，从中选取 \(k\) 个点；

下面是把 \(m\) 取出来建的虚树，假设 \(m = 8\) 虚树且 (\(k = 4,5,8\)） 所走的路径如图

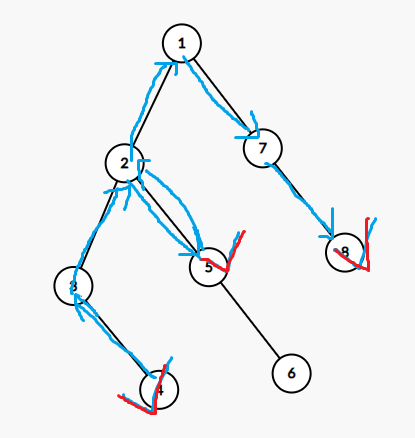
发现由 4~8 的路径上的边只走了一遍，而只有 2 ~ 5 之间的边走了两边，因为小D不会傻到去走两边 1 ~ 8 之间的路径两边然后再回来去拿 5 的物品，所以我们就的出了所选的 $k $ 个点构成另一颗虚树，它的主链只会走一次，而它的支链会走两边 (主链支链定义取自有机化学)

由于期望复杂度要求线性，所以我们把答案拆成两部分来做

我们可以通过虚树上的边都走两次然后再减去直径上的边就好了

求一条边在虚树上的方案数？

和上面的题一个样， \(\tbinom{m}{k} - \tbinom{a}{k} - \tbinom{m - a}{k}\)

然后乘以每个边的权值就好了

注意：这条边左边点的个数和右边点的个数可以通过 \(dfs\) 求出每个点的子树大小求出

然后剩下的就是求虚树上的直径长度问题了

那么我们枚举每一对 \((i, j)\)，计算他们能够成为直径的概率

考虑第一次以 \(i\) 为根 \(dfs\)，那么我们只需要剩下的 \(k − 2\) 个节点到 \(i\) 的距离都比 \(j\) 近，然后再考虑以 \(j\) 为根进行 \(dfs\)，即到 \(j\) 的距离也比 \(i\) 近即可。于是我们便枚举剩下的所有结点，然后找到合法的结点假设有 \(m\) 个，那么共有 \(\tbinom{m}{k - 2}\) 种方案满足 (i, j) 成为直径

两点间的距离：两点的深度减去两倍的它们 \(LCA\) 的深度

注意: 有多个长度相同的直径我们要选取标号最小的那个