树链剖分
树链剖分
发现漏了树剖的笔记,来补作业了==
有关dfs序
老玩意,就是遍历树的时候每个节点被搜到的顺序
我们画出一棵树,模拟一下搜索过程可以得出这么一个结论:
一棵子树在dfs序上是连续的一段
每个节点对应着一个区间,对节点操作就可以用线段树维护了
树链剖分
概念:
重儿子(节点):子树结点数目最多的结点
轻儿子(节点):除了重儿子以外的结点
重边:父亲结点和重儿子连成的边
轻边:父亲节点和轻儿子连成的边
重链:由多条重边连接而成的路径
轻链:由多条轻边连接而成的路径
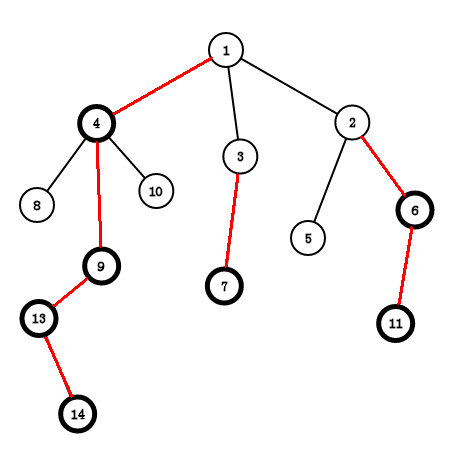
图来自:Ivanovcraft
根据上面的定义:
我们可以得出:加粗的黑色节点是重儿子,其余的都是轻儿子(叶子节点没有重儿子,非叶子节点只有一个重儿子)
红的是重边,黑的是轻边
几个变量
\(f[u]\) 结点 \(u\) 的父亲节点
\(dep[u]\) 保存结点 \(u\) 的深度值
\(siz[u]\) 保存以 \(u\) 为根的子树节点个数
\(son[u]\) \(u\) 的重儿子
\(pre[u]\) 当前 \(dfs\) 标号在树中所对应的节点
\(top[u]\) 当前节点所在链的顶端节点
\(dfn[u]\) 树中每个节点剖分以后的新编号(DFS的执行顺序)
第一个大法师
预处理,求 \(f[u]\),\(dep[u]\),\(son[u]\) ,\(siz[u]\)
看代码应该就能理解
void dfs(int x,int f,int d){
dep[x] = d,fa[x] = f,siz[x] = 1;
for(int i = head[x]; i;i = e[i].nxt){
int v = e[i].v;
if(v != fa[x]){
dfs(v, x, d + 1);
siz[x] += siz[v];
if(!son[x]||siz[son[x]] < siz[v])
son[x] = v;
}
}
}
第二个大法师
把树剖了
按照每个点的重儿子向下搜,跑出一个 \(dfs\) 序,连续的 一段 \(dfs\) 就是一条重链,顺便存下在这个 \(dfs\) 序下,每个\(dfs\) 序在原树中的标号 \(pre[u]\)(方便建线段树的时候确定每个点在原树中的位置)
跑出来应该是这样的
void dfs2(int x,int tp){
dfn[x]=++cnt,pre[cnt] = x,top[x] = tp;
if(son[x]) dfs2(son[x],tp);
for(int i = head[x]; i; i = e[i].nxt){
int v = e[i].v;
if(v != fa[x]&&v != son[x]) dfs2(v,v);
}
}
线段树维护
见很多博客都没有写这个(一开始也是没有搞懂),所以这里提一下
线段树维护的是每个重链的信息,也就是说线段树的标号对应着第二个 \(dfs\) 跑出来的 \(dfs\) 序,这样每条重链上的信息就可以直接用线段树维护了(因为它们的 \(dfs\) 序都是连续的)例如:求一条重链上的点权值和,直接利用线段树区间加就好了
求树上两点之间最短路径
如果两点在一条重链上:直接区间利用两点的 \(dfs\) 序区间求和就好了
如果不在一条重链上:先把两点跳到一条重链上,再求两点在这条重链上的距离就好了
也可以利用这个方法求两点的 \(LCA\)
int asksum(int x,int y){
int ans = 0;
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]]) swap(x,y);
ans = (ans + Seg::query(1, 1, n, dfn[top[x]], dfn[x])) % mod;
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x,y);
ans = (ans + Seg::query(1, 1, n, dfn[x], dfn[y])) % mod;
return ans;
}
更改两点间最短路径上的值
和上面一个样,只不过把求和变成了区间更改
void change_sum(int x,int y,int k){
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]]) swap(x,y);
Seg::update(1, k, 1, n,dfn[top[x]], dfn[x]);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x,y);
Seg::update(1, k, 1, n,dfn[x], dfn[y]);
}
求一个点子树的值
每条重链的 \(dfs\) 是连续的,所以每个点的子树的 \(dfs\) 也是连续的(手摸一下),所以求每个点子树的值,只需要求这个点的 \(dfn[x]\) 序到 \(dfn[x] + siz[x] - 1\) 就好了
int query_tree(int x){
return Seg::query(1, 1, n, dfn[x],dfn[x] + siz[x] - 1);
}
时间复杂度:
\(O(nlog^2n)\)
树链剖分模板
已知一棵包含 \(N\) 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作 1:将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)
操作 2:求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和。
操作 3: 将以 \(x\) 为根节点的子树内所有节点值都加上 \(z\)
操作 4: 求以 \(x\) 为根节点的子树内所有节点值之和
/*
work by:Ariel
*/
#include <iostream>
#include <cstdio>
#define N 100005
#define ll long long
#define lson rt << 1
#define rson rt << 1|1
using namespace std;
int n,m,r;
ll mod;
int pre[N],w[N],dep[N],fa[N],son[N],siz[N],top[N],dfn[N],dfn2[N],cnt;
ll read(){
ll x = 0,f = 1;char c = getchar();
while(c < '0'||c > '9'){if(c == '-')f = -1;c = getchar();}
while(c >= '0'&&c <= '9'){x = x*10 + c - '0';c = getchar();}
return f*x;
}
namespace Seg{
struct Tree{
int sum,len,lazy;
}tree[N << 1];
void push_up(int rt){
tree[rt].sum = (tree[lson].sum + tree[rson].sum) % mod;
}
void build(int rt,int l,int r){
tree[rt].len = r - l + 1;
if(l == r){
tree[rt].sum = w[pre[l]];
return;
}
int mid = (l + r)>>1;
build(lson, l, mid);
build(rson, mid + 1, r);
push_up(rt);
}
void pushdown(int rt) {
if (tree[rt].lazy){
tree[lson].sum = (tree[lson].sum + (tree[rt].lazy * tree[lson].len) % mod) % mod;
tree[rson].sum = (tree[rson].sum + (tree[rt].lazy * tree[rson].len) % mod) % mod;
tree[lson].lazy = (tree[lson].lazy + tree[rt].lazy) % mod;
tree[rson].lazy = (tree[rson].lazy + tree[rt].lazy) % mod;
tree[rt].lazy = 0;
}
}
void update(int rt,int k,int l,int r,int L,int R){
if(l >= L && r <= R){
tree[rt].sum = (tree[rt].sum + (k * tree[rt].len) % mod) % mod;
tree[rt].lazy = (tree[rt].lazy + k) % mod;
return;
}
pushdown(rt);
int mid = (l + r) >> 1;
if(mid >= L) update(lson, k, l, mid, L, R);
if(mid < R) update(rson, k, mid+1, r, L, R);
push_up(rt);
}
int query(int rt,int l,int r,int L,int R){
if(l >= L&& r <= R) return tree[rt].sum;
pushdown(rt);
int mid = (l + r)>>1,ans = 0;
if(L <= mid) ans = (ans + query(lson,l,mid,L,R) % mod) % mod;
if(mid < R) ans = (ans + query(rson,mid + 1,r,L,R) % mod) % mod;
return ans;
}
}
namespace Cut {
struct edge{
int v,nxt;
}e[N << 1];
int head[N],js;
void add_edge(int u,int v){
e[++js].v = v;e[js].nxt = head[u];head[u] = js;
}
void dfs(int x,int f,int d){
dep[x] = d,fa[x] = f,siz[x] = 1;
for(int i = head[x]; i;i = e[i].nxt){
int v = e[i].v;
if(v != fa[x]){
dfs(v, x, d + 1);
siz[x] += siz[v];
if(!son[x]||siz[son[x]] < siz[v])
son[x] = v;
}
}
}
void dfs2(int x,int tp){
dfn[x]=++cnt,pre[cnt] = x,top[x] = tp;
if(son[x]) dfs2(son[x],tp);
for(int i = head[x]; i; i = e[i].nxt){
int v = e[i].v;
if(v != fa[x]&&v != son[x]) dfs2(v,v);
}
}
void change_tree(int x,int k){
Seg::update(1 , k, 1, n, dfn[x],dfn[x] + siz[x] - 1);
}
int query_tree(int x){
return Seg::query(1, 1, n, dfn[x],dfn[x] + siz[x] - 1);
}
void change_sum(int x,int y,int k){
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]]) swap(x,y);
Seg::update(1, k, 1, n,dfn[top[x]], dfn[x]);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x,y);
Seg::update(1, k, 1, n,dfn[x], dfn[y]);
}
int asksum(int x,int y){
int ans = 0;
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]]) swap(x,y);
ans = (ans + Seg::query(1, 1, n, dfn[top[x]], dfn[x])) % mod;
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x,y);
ans = (ans + Seg::query(1, 1, n, dfn[x], dfn[y])) % mod;
return ans;
}
}
int main() {
n = read(), m = read(),r = read(),mod = read();
for (int i = 1; i <= n; i++) w[i] = read();
for (int i = 1, x, y; i <= n - 1; i++) {
x = read(), y = read();
Cut::add_edge(x, y);
Cut::add_edge(y, x);
}
Cut::dfs(r, 0, 1);
Cut::dfs2(r, r);
Seg::build(1, 1, n);
for (int i = 1, opt, x, y,z; i <= m; i++) {
opt = read();
if (opt == 1) x = read(), y = read(),z = read(),Cut::change_sum(x, y, z);
if (opt == 2) x = read(),y = read(),printf("%lld\n", Cut::asksum(x, y));
if (opt == 3) x = read(),y = read(),Cut::change_tree(x,y);
if (opt == 4) x = read(),printf("%lld\n", Cut::query_tree(x));
}
}


