整数划分模型
整数划分模型
经典问题
1:求把 n 划分成 k 个正整数的方案数?
2:求把 n 划分成互不相同 k 个正整数的方案数?
3:求把 n 划分成 k 个不大于 m 的互不相同正整数的方案数?
4:求把 n 划分成 k 个奇数的方案数?
发现这类为题都是把一个整数划分成 \(k\) 个有要求的正整数的方案数
先从简单开始,考虑最为暴力的Dp
状态:
设 \(dp[i][j][sum]\) 表示前 \(i\) 个数,和为 \(sum\) 的方案数是多少,答案就是 \(dp[n][k][n]\)
转移:
考虑下一个数选几个来转移, $ t $ 表示当前 \(i\) 这个数选了多少个
时间复杂度:
状态:\(n*k*n\)
转移: \(O(sum/i)\)
均摊的话: \(O(n*k*n*log(n))\)
本质是个完全背包,可以做到 \(O(n*k*n)\) 不会
接下来就是神仙操作了……
我们直接设 \(dp[i][j]\) 表示把 \(i\) 划分成 \(j\) 个数的方案数
可以得到下面这个式子:
???
咋来的??
把 \(i\) 分成 \(j\) 个数的方案数等于把 \(i-j\) 分成 \(j\) 个数的方案数+把 \(i-1\) 分成 \(j-1\) 个数的方案数
???
啥啊这是
这里单靠瞅式子已经不能说服自己了
上图
以下是 \(dp[22][4]\) 的两类情况: 考虑有没有 \(1\) 的部分
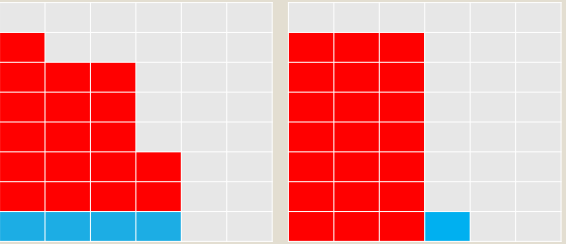
划分的数,分别对应着四个矩形的高度,第一个图是7,6,6,3 第二个图是7,7,7,1
考虑去掉蓝色的部分
发现左边去掉蓝色部分后状态成了 \(f[i - j][j]\)
右边去掉蓝色的部分后状态成了 \(f[i - 1][j - 1]\)
所以就不难看出:\(f[i][j]\) 是由 \(f[i-j][j]\) 和 \(f[i-1][j-1]\) 转移过来的
来个栗题
T1
求把 \(n\) 划分成互不相同 \(k\) 个正整数的方案数
solution
同样先考虑暴力
状态:
设 \(dp[i][j][sum]\) 前 \(i\) 个数,选了 \(j\) 个数,和为 \(sum\) 的方案数是多少
转移:
考虑第 \(i\) 个数选不选
转移:
实际是就是个01背包
时间复杂度:
\(O(n*k*n)\)
正解
还是直接设 \(dp[i][j]\) 表示把 \(i\) 划分成 \(j\) 个数的方案数
\(dp[i][j]=dp[i-j][j]+dp[i-j][j-1]\)
考虑去掉蓝色的部分
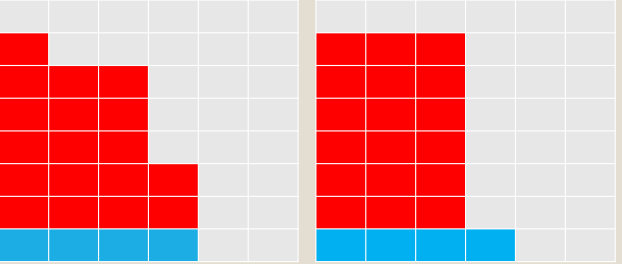
同样要考虑 \(1\) 的情况,但与上题不同的是这里第一维是 \([i-j]\),表示当前数加上 \(j\) 这一行,并且新多了一行
因为是整行都加,所以就避免了重复的情况
T2
求把 \(n\) 划分成 \(k\) 个不大于 \(m\) 的互不相同正整数的方案数
背包方法和上题一个样,枚举第 \(i\) 个数选不选就好了;
而正解也只需要把超过 \(m\) 的那些不合法的删掉就好了
\(N = 20,k = 4,m = 6\) 不合法方案
最后一个的减法就是要把不合法的情况减掉,直接减掉不符合条件的那一列
看个栗题
给定一个杠杆,等距均匀分布一共 \(2*n+1\) 个等重质点,支点在 \(n+1\) 处,求拿走 \(k\) 个质点后使杠杆仍然保持平衡的方案数 \(mod~~p\) 的值
化简:
\(-n => n\) 中求选 \(k\) 个不同的数,和为 0 的方案数
solution
根据上面整数划分原理
求出来 \(f[i][j]\) 表示选出 \(j\) 个数和为 \(i\) 的方案数,然后枚举其中一端拿走几个 \(a\),以及拿走的数的重量之和 \(x\),把\(f[x][a]*f[x][k-a]\) 累加之和就是最后的答案了
然后就变成了上面的把 \(n\) 划分成互不相同 \(k\) 个正整数的方案数
算 \(f\) 的复杂度和统计答案的复杂度均是 \(O(n*k*k)\)
把 \(n\) 划分成 \(k\) 个奇数或者 \(k\) 个偶数的方案数
状态:
\(g[i][j]\) :将 \(i\) 划分为 \(j\) 个偶数
\(f[i][j]\): 将 \(i\) 划分为 \(j\) 个奇数
转移:
\(g[i][j] = f[i - j][j]\)
联想上面的图,偶数可以由将每个奇数减1就都成了偶数
\(f[i][j] = f[i - 1][j - 1] + g[i - j][j]\)
奇数的话
分两种情况
奇数有可能右边有个单独的1,这就可能由 \(f[i - 1][j - 1]\) 来转移过来(新填了一行正好有个单独的1)
当然一般情况为 \(g[i - j][j]\) 每个偶数-1转移过来
关于整数划分模型
就是分类讨论罢了,注意不要漏掉情况,也不能情况计算重叠(max,min可以重叠) ,每个 \(dp\) 值可以用以前的\(dp\) 值表示出来,保证要递归到已经求好的 \(dp\) 值中


