差分约束(刷题)
差分约束#
来自Kersen
给定 个变量和 个不等式,每个不等式形如 ,求 的最大值。
例:
①
②
③
④
⑤
然后经过认真的瞎搞计算就变成了这个鸭子:
1、③
2、②+⑤
3、①+④+⑤
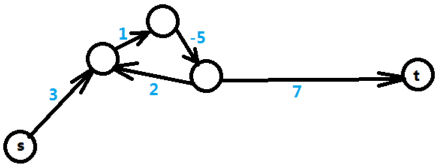
对于每个不等式 ,对结点 和 建立一条 的有向边,
边权为 ,求 的最大值就是求 到 的最短路
求最大值的时候把全部的不等式都化成: 的形式;
然后建由 指向 边权为 的边,跑最短路;
求最小值的时候把全部的不等式都化成:$$
差分约束系统的解有两种特殊情况:#
1. 最大值不存在
存在负环,用 判负环
2. 的值无限大
图不连通…………
不等式标准化#
1.如果给出的既有 又有
如果需要求的是两个变量差的最大值,那么需要将所有不等式转变成"<="的形式,建图后求最短路;
相反,如果需要求的是两个变量差的最小值,那么需要将所有不等式转化成">=",建图后求最长路。
2.如果有形如 的等式
我们可以将它转化成以下两个不等式:
①
②
再通过上面的方法将其中一种不等号反向,建图即可。
3.如果遇到不带等号的,
我们可以将它转化成""或者""的形式,即 形式就可以做了...
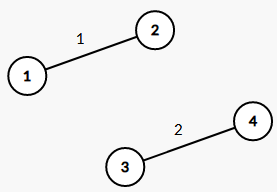
Intervals#
给定多个区间,要求每个区间选一定数量的数,求所选的数至少为多少
solution#
差分约束板子
可以推出下面的不等式
/*
work by:Ariel_
*/
#include <iostream>
#include <cstdio>
#include <queue>
#include <iostream>
#include <cstring>
using namespace std;
const int M = 1e6 + 11;
int read(){
int x = 0,f = 1;char c = getchar();
while(c < '0'||c > '9'){if(c == '-')f = -1;c = getchar();}
while(c >= '0'&&c <= '9'){x = x*10 + c - '0';c = getchar();}
return f*x;
}
struct edge{
int v,nxt,w;
}e[M << 1];
int cnt,head[M];
void add_edge(int u,int v,int w){
e[++cnt] = (edge){v, head[u], w};
head[u] = cnt;
}
int T, n, maxn = -0x3f3f3f3f,dis[M],vis[M];
queue<int> q;
void spfa(){
memset(dis, -0x3f, sizeof(dis));
memset(vis, 0, sizeof(vis));
dis[0] = 0,vis[0] = 1;
q.push(0);
while(!q.empty()){
int u = q.front();
q.pop();vis[u] = 0;
for(int i = head[u]; i;i = e[i].nxt){
int v = e[i].v;
if(dis[v] < dis[u] + e[i].w){
dis[v] = dis[u] + e[i].w;
if(!vis[v]){
vis[v] = 1;
q.push(v);
}
}
}
}
}
int main(){
n = read();
for(int i = 1,a,b,c;i <= n; i++){
a = read(),b = read(),c = read();
add_edge(a, b + 1, c);
maxn = max(b + 1,maxn);
}
for(int i = 1;i <= maxn; i++){
add_edge(i - 1, i, 0);
add_edge(i,i - 1, -1);
}
spfa();
printf("%d\n", dis[maxn]);
}
出纳员问题#
题意较长……没时间写了,看链接把
solution#
/*
work by:Ariel_
*/
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
const int M = 1e5 + 10;
const int eqs = 1e-10;
int read(){
int x = 0,f = 1;char c = getchar();
while(c < '0'||c > '9'){if(c == '-')f = -1;c = getchar();}
while(c >= '0'&&c <= '9'){x = x*10 + c - '0';c = getchar();}
return f*x;
}
int T,r[25],a[1010],n,dis[100010],num[100010];
bool vis[100010];
struct edge{
int v, nxt, w;
}e[M];
int js,head[M];
void add_edge(int u,int v,int w){
e[++js] = (edge){v,head[u],w};
head[u] = js;
}
void clear(){
js = 0;
memset(head, 0, sizeof(head));
memset(dis, 0x3f, sizeof(dis));
memset(vis, 0, sizeof(vis));
}
queue<int>q;
bool check(int x){
clear();
add_edge(0, 24, x);
for (int i = 1; i <= 24; i++){
add_edge(i, i - 1, 0);
add_edge(i - 1, i, num[i]);
if(i > 8) add_edge(i, i - 8, -r[i]);
else add_edge(i, i + 16, x - r[i]);
}
q.push(0), dis[0] = 0, vis[0] = 0;
while(!q.empty()){
int u = q.front();
q.pop();
vis[u] = 0;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v, w = e[i].w;
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
js++;
if(!vis[v]){
vis[v] = 1;
q.push(v);
}
if(js > 2000) return 0;
}
}
}
return dis[24] == x;
}
int main(){
T = read();
while(T--){memset(num, 0, sizeof(num));
for (int i = 1;i <= 24; i++)r[i] = read();
n = read();
for (int i = 1, x;i <= n; i++){
x = read() + 1;
num[x]++;
}
int l = 0, r = n, ans = 0x3f3f3f3f;
while(l <= r){
int mid = (r + l) >> 1;
if(check(mid)) ans = mid, r = mid - 1;
else l = mid + 1;
}
if(ans == 0x3f3f3f3f) cout << "No Solution" << endl;
else cout << ans << endl;
}
}
糖果#
一大串不等式关系,跑差分约束
/*
work by:Ariel_
*/
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
#define int long long
const int M = 1e6 + 10;
int read(){
int x = 0,f = 1;char c = getchar();
while(c < '0'||c > '9'){if(c == '-')f = -1;c = getchar();}
while(c >= '0'&&c <= '9'){x = x*10 + c - '0';c = getchar();}
return f*x;
}
struct edge{
int v,nxt,w;
}e[M << 1];
int cnt,head[M];
void add_edge(int u,int v,int w){
e[++cnt] = (edge){v, head[u], w};
head[u] = cnt;
}
int n, k, dis[M], ans, tot[M];
bool vis[M];
signed main(){
n = read(),k = read();
for(int i = 1, x, a, b;i <= k; i++){
x = read(),a = read(),b = read();
if(x == 1)add_edge(a, b, 0),add_edge(b, a, 0);
if(x == 2){
if(a == b){
printf("-1");return 0 ;
}
add_edge(a, b, 1);
}
if(x == 3)add_edge(b, a, 0);
if(x == 4){
if(a == b){
printf("-1");return 0;
}
add_edge(b, a, 1);
}
if(x == 5)add_edge(a, b, 0);
}
for(int i = n; i >= 1; i--)add_edge(0, i, 1);
std::queue<int> q;
q.push(0);
vis[0] = 1,dis[0] = 0;
while(!q.empty()){
int u = q.front();q.pop();
vis[u] = 0;
if(tot[u]== n - 1){
printf("-1");return 0;
}
tot[u]++;
for(int i = head[u]; i;i = e[i].nxt){
int v = e[i].v;
if(dis[v] < dis[u] + e[i].w){
dis[v] = dis[u] + e[i].w;
if(!vis[v])vis[v] = 1,q.push(v);
}
}
}
int ans = 0;
for(int i = 1;i <= n; i++) ans += dis[i];
printf("%lld", ans);
}
布局 Layout#
既有 又有 处理如上
两种特殊情况
/*
work by:Ariel_
*/
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
const int M = 10100;
int read(){
int x = 0,f = 1;char c = getchar();
while(c < '0'||c > '9'){if(c == '-')f = -1;c = getchar();}
while(c >= '0'&&c <= '9'){x = x*10 + c - '0';c = getchar();}
return f*x;
}
struct edge{
int v, nxt, w;
}e[M << 1];
int js,head[M];
void add_edge(int u,int v,int w){
e[++js] = (edge){v,head[u],w};
head[u] = js;
}
int dis[M],tot[M], n, ml,md;
bool vis[M];
int spfa(int x){
memset(dis,0x7f/3,sizeof(dis));
memset(vis,0,sizeof(vis));
memset(tot,0,sizeof(tot));
queue<int> q;
vis[x] = 1;q.push(x);dis[x] = 0;
while(!q.empty()){
int u = q.front();q.pop();
vis[u] = 0;tot[u]++;
if(tot[u] > n) return -1;
for(int i = head[u]; i; i = e[i].nxt){
int v = e[i].v;
if(dis[v] > dis[u] + e[i].w){
dis[v] = dis[u]+ e[i].w;
if(!vis[v]){
q.push(v);
vis[v] = 1;
}
}
}
}
if(dis[n] > 1e8)return -2;
return dis[n];
}
int main(){
n = read(),ml = read(),md = read();
for(int i = 1,u, v, w;i <= ml; i++){
u = read(),v = read(),w = read();
add_edge(u, v, w);
}
for(int i = 1, u, v, w;i <= md; i++){
u = read(),v = read(),w = read();
add_edge(v, u, -w);
}
for(int i = 1;i < n; i++)add_edge(i + 1, i, 0);
for(int i = 1;i <= n; i++)add_edge(0, i, 0);
if(spfa(0) <= -1)printf("%d",spfa(spfa(0)));
else printf("%d",spfa(1));
}




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 25岁的心里话