A*算法路径规划仿真
matlab代码
1、建立栅格地图
MAX0 = [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 1 1 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0
0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
0 0 1 1 0 0 1 1 1 1 1 1 1 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0
0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1
0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 0 1 1 0 0 1 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] ;
%%% 通道设置为 0 ;障碍点设置为 1 ;起始点设置为 2 ;目标点设置为 -1 。
MAX=rot90(MAX0,3); %%%设置0,1摆放的图像与存入的数组不一样,需要先逆时针旋转90*3=270度给数组,最后输出来的图像就是自己编排的图像
MAX_X=size(MAX,2); %%% 获取列数,即x轴长度
MAX_Y=size(MAX,1); %%% 获取行数,即y轴长度
2、基于A*算法路径规划
% START ALGORITHM 开始算法
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
while((xNode ~= xTarget || yNode ~= yTarget) && NoPath == 1) %%% 判断当前点是否等于目标点
% plot(xNode+.5,yNode+.5,'go');
% xnode=xNode,ynode=yNode %%%****输出当前节点,用来学习了解A*算法的运算过程**** ///不需要知道过程可注释掉///
exp_array=expand_array(xNode,yNode,path_cost,xTarget,yTarget,CLOSED,MAX_X,MAX_Y); %%% 不在关闭列表的子节点,(x,y,gn,hn,fn),列数是个数
exp_count=size(exp_array,1); %%% 可选择的子节点个数
%UPDATE LIST OPEN WITH THE SUCCESSOR NODES
%OPEN LIST FORMAT
%--------------------------------------------------------------------------
%IS ON LIST 1/0 |X val |Y val |Parent X val |Parent Y val |h(n) |g(n)|f(n)|
%--------------------------------------------------------------------------
%EXPANDED ARRAY FORMAT 扩展阵列格式
%--------------------------------
%|X val |Y val ||h(n) |g(n)|f(n)|
%--------------------------------
for i=1:exp_count %%% 把exp_array内的元素添加到 开启列表 里面
flag=0; %%% 将exp_array内的点的标志位设为0
for j=1:OPEN_COUNT %%% OPEN_COUNT 从1开始,自加
if(exp_array(i,1) == OPEN(j,2) && exp_array(i,2) == OPEN(j,3) ) %%%判断可选子节点是否与OPEN[]中的点相同
OPEN(j,8)=min(OPEN(j,8),exp_array(i,5)); %%%如果相同,比较两个fn的值的大小,并将fn小的坐标点赋值给OPEN(j,8)
if OPEN(j,8)== exp_array(i,5) %%% 表示,上一步比较中 exp_array(i,5)小,则把exp_array(i,:)中的值赋给OPEN
%UPDATE PARENTS,gn,hn
OPEN(j,4)=xNode;
OPEN(j,5)=yNode;
OPEN(j,6)=exp_array(i,3);
OPEN(j,7)=exp_array(i,4);
end;%End of minimum fn check
flag=1; %%%将与OPEN相同的flag=0
end;%End of node check
% if flag == 1
% break;
end;%End of j for
if flag == 0
OPEN_COUNT = OPEN_COUNT+1;
OPEN(OPEN_COUNT,:)=insert_open(exp_array(i,1),exp_array(i,2),xNode,yNode,exp_array(i,3),exp_array(i,4),exp_array(i,5));
end;%End of insert new element into the OPEN list
end;%End of i for
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%END OF WHILE LOOP
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Find out the node with the smallest fn 找出fn最小的节点
index_min_node = min_fn(OPEN,OPEN_COUNT,xTarget,yTarget); %%%选出fn最小那一行,将行数赋给 index_min_node
if (index_min_node ~= -1)
%Set xNode and yNode to the node with minimum fn 将xNode和yNode设置为最小fn的节点
xNode=OPEN(index_min_node,2);
yNode=OPEN(index_min_node,3);
path_cost=OPEN(index_min_node,6);% Update the cost of reaching the parent node 更新到达父节点的成本 gn
%Move the Node to list CLOSED 将节点移动到列表CLOSED
CLOSED_COUNT=CLOSED_COUNT+1;
CLOSED(CLOSED_COUNT,1)=xNode;
CLOSED(CLOSED_COUNT,2)=yNode;
OPEN(index_min_node,1)=0;
% CLOSED %%%****输出CLOSE[],用来学习了解A*算法的运算过程**** ///不需要知道过程可注释掉///
% OPEN %%%****输出OPEN[],用来学习了解A*算法的运算过程**** ///不需要知道过程可注释掉///
else
%No path exists to the Target!!
NoPath=0;%Exits the loop!
end;%End of index_min_node check
end;%End of While Loop
%Once algorithm has run The optimal path is generated by starting of at the
%last node(if it is the target node) and then identifying its parent node
%until it reaches the start node.This is the optimal path
i=size(CLOSED,1); %%%CLOSE里面的长度
Optimal_path=[]; %%%路径数组
xval=CLOSED(i,1); %%%把CLOSE最后一组数提出来,最后一组数为目标点
yval=CLOSED(i,2);
i=1;
Optimal_path(i,1)=xval; %%%把目标点的坐标赋给 路径数组的 第一组
Optimal_path(i,2)=yval;
i=i+1;
if ( (xval == xTarget) && (yval == yTarget)) %%%检测CLOSE最后一组是否为目标点
inode=0;
%Traverse OPEN and determine the parent nodes 遍历OPEN并确定父节点
parent_x=OPEN(node_index(OPEN,xval,yval),4); %node_index returns the index of the node node_index返回节点的索引
parent_y=OPEN(node_index(OPEN,xval,yval),5);%%% 将当前点的父节点提出来
while( parent_x ~= xStart || parent_y ~= yStart) %%% 判断父节点是否为起始点
Optimal_path(i,1) = parent_x; %%% 不是 则将父节点送给路径数组
Optimal_path(i,2) = parent_y;
%Get the grandparents:-)
inode=node_index(OPEN,parent_x,parent_y);
parent_x=OPEN(inode,4);%node_index returns the index of the node
parent_y=OPEN(inode,5);
i=i+1;
end;
toc
j = size(Optimal_path,1) + 1;
Optimal_path(j,1) = xStart;
Optimal_path(j,2) = yStart; %%%把起始点加进去
% j=size(Optimal_path,1);
%Plot the Optimal Path!
p=plot(Optimal_path(j,1)+.5,Optimal_path(j,2)+.5,'bo'); %%
j=j-1;
for i=j:-1:1
pause(.25);
set(p,'XData',Optimal_path(i,1)+.5,'YData',Optimal_path(i,2)+.5);
drawnow ;
end;
plot(Optimal_path(:,1)+.5,Optimal_path(:,2)+.5,'linewidth',2); %5%绘线
%%%%%%%%% 计算直线路径的长度
S_line=0;
for i=1:j
s1 = distance(Optimal_path(i,1),Optimal_path(i,2),Optimal_path(i+1,1),Optimal_path(i+1,2));
S_line=s1 + S_line;
end
sprintf('折线路径距离为')
S_line
else
pause(1);
h=msgbox('Sorry, No path exists to the Target!','warn');
uiwait(h,5);
end
3、实验结果
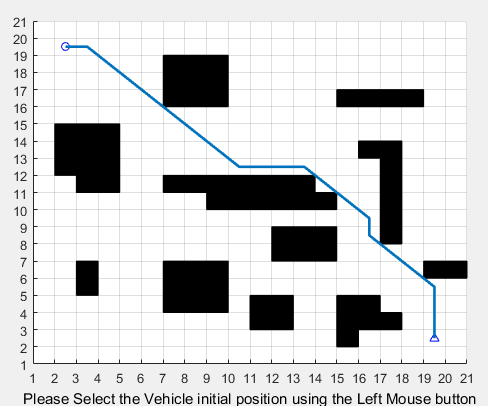



 浙公网安备 33010602011771号
浙公网安备 33010602011771号