2023.6.20 NOI模拟赛总结

仍然抽象的一集。

1.时间安排

7:10~8:30

T1：安排树上点权成为排列，最大化点权递增的路径，看上去很难做。

T2：还是树上问题，给点权和边权打乱的序列，对于每种1到n的长度的路径求出可能的最大值，感觉是个贪心+构造。

T3：一眼60分的 \(O(n^4)\) DP，并且剩下的就是正解，但是状态数已经是 \(O(n^2)\)，离线枚举起点是 \(O(n^2)\)，不知道还能做到怎么更优。

先随便推了推T1，感觉可能是和树的直径有关，先找一个直径染成从1开始的递增，但是样例1就hack掉了。然后试着把比较适中的值填到直径上，确实可以过两个小样例，但是太难刻画这个过程了。

然后推了推T2，没有一眼看出来的性质，就先去写T3了。

T3的DP细节还是有一些的，需要考虑右部点是否已经被钦定，不过还是比较顺利过了大样例。

8:30~10:20

看了一眼T2的大样例，发现似乎是最大的 \(k\) 个的和的形式，打了一下表，发现不是无解的情况绝大部分都是最大的 \(k\) 个数的和。

于是大胆猜测可以先钦定最大的 \(k\) 个数作为1到 \(n\) 路径上的边权，然后剩下的数中选出来 \(k\) 个作为这条路径，剩下的前一半小的作为剩下没确定父亲的点的父亲，依次钦定，最后剩下的作为边权。

当无法选出 \(k\) 个点作为路径时，就把最大的 \(k\) 个其中比较小的拿出来并入路径中，容易证明这样一定最优。

当可以选的点数大于等于 \(k\) 时，相当于在这个递增序列中选择长度为 \(k\) 的子序列，使得剩下的能构成一棵合法的树，考场上觉得贪心选最大的就行了。

写完调了很久边界过了大样例，感觉大样例很强就选择了相信。

10:20~12:00

拼了个T1的状压暴力跑路，什么性质都推不出来。

result:

T1:24 T2:0 T3:60

2.总结

T1：

仍然不知道为什么要选重心，这题就是不会结论状压暴力会结论轻松100。

放一下题解，不想自己码字了。

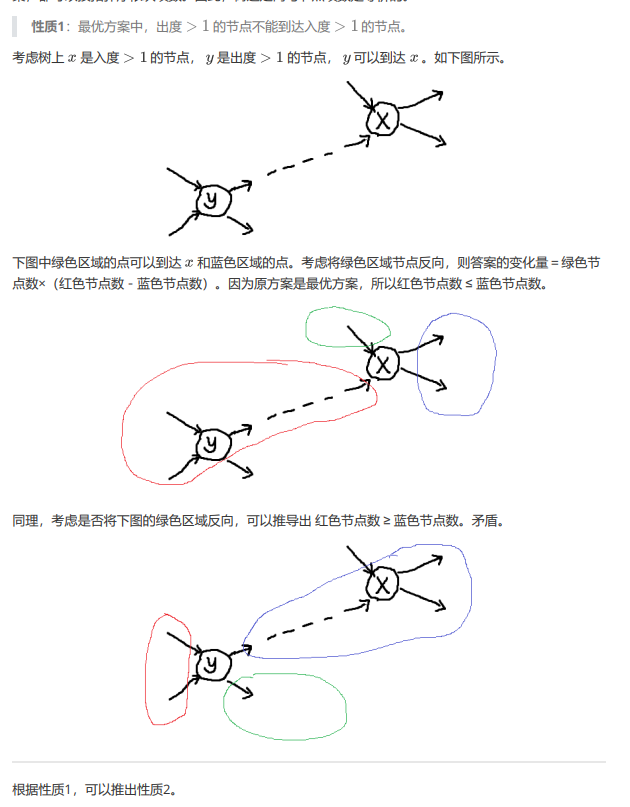
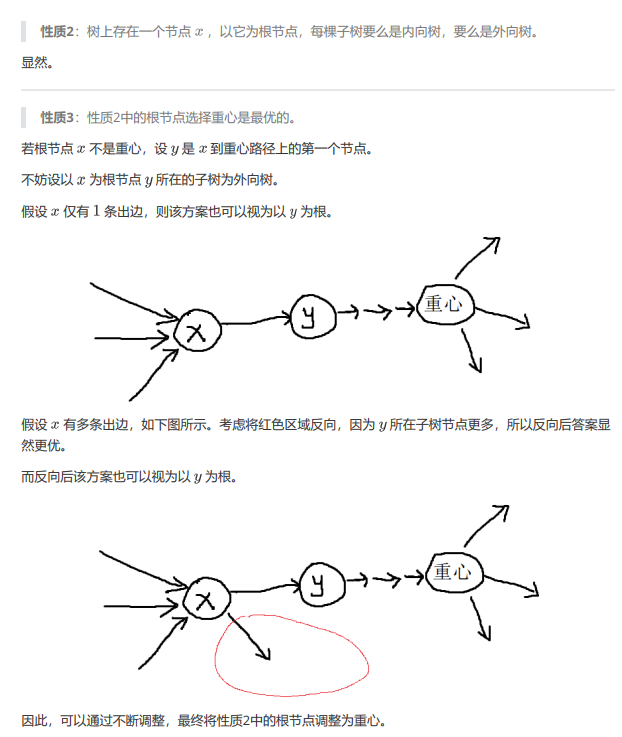
然后找到重心，之后的问题就等价于有若干个数，分配到两个集合使得两个集合内的数的和的差的绝对值最小，经典bitset优化01背包，因为总和是 \(n\) 所以不同的权值种类数是 \(\sqrt n\) 级别，用一下二进制分组的思想就可以做到 \(O(\frac{n^{1.5}}{w})\)。

more and more 结论题，what should I do.

T2：

我的构造在可以选的点数大于 \(k\) 时就会出问题，原因在于贪心选最小的可能让一些点无法取到1作为父亲而无解，所以我要做的是让这个子序列尽量小的同时尽量大，这显然是不可做的。

仍然是猜结论然后根据结论构造（猜结论题怎么这么多……）、

还是放一下题解，不想码字。

T3：

可以把DP过程看成跑有向图的最长路，分治优化求解的过程，还是放题解，不会证复杂度。