攻防世界 reverse 进阶 notsequence

notsequence  RCTF-2015

 

 

 关键就是两个check函数

 1 signed int __cdecl check1_80486CD(int a1[])
 2 {
 3   signed int j; // [esp+0h] [ebp-14h]
 4   int t; // [esp+4h] [ebp-10h]
 5   int i; // [esp+8h] [ebp-Ch]
 6   signed int k; // [esp+Ch] [ebp-8h] k=0 i=0  a[0]=1
 7                 //                   k=1 i=1  a[1]+a[2]=2      a[1]=1 a[2]=1
 8                 //                   k=2 i=3  a[3]+a[4]+a[5]=4
 9                 //                   k=3 i=6  a[6]+a[7]+a[8]+a[9]=8
10 
11   k = 0;
12   for ( i = 0; i <= 1024 && a1[i]; i = k * (k + 1) / 2 )// i是（1，2，3，4，）等差数列和
13   {
14     t = 0;                                      // i:0 1 3 6 10 15  (递增k)
15     for ( j = 0; j <= k; ++j )
16       t += a1[j + i];                           // input[i]后面k个数的和
17     if ( 1 << k != t )                          // 2`k要==t-->sum(input[i],input[i+k])
18       return -1;                                // k==20
19     ++k;
20   }
21   return k;
22 }

可以抽象成一个二维结构，有[k] 行（第一行k=0），每行开头为第k*(k+1)/2个数，check1函数检测每一行求和结果为2`k    

 

再看check2

 1 signed int __cdecl check2_8048783(int a1[], signed int k_20)
 2 {
 3   int k; // [esp+10h] [ebp-10h]
 4   int t; // [esp+14h] [ebp-Ch]
 5   signed int i; // [esp+18h] [ebp-8h]
 6   int j; // [esp+1Ch] [ebp-4h]
 7 
 8   j = 0;
 9   for ( i = 1; i < k_20; ++i )                  // i=1,2,3
10   {
11     t = 0;
12     k = i - 1;                                  // k=0,1,2,3
13     if ( !a1[i] )
14       return 0;
15     while ( k_20 - 1 > k )                      // k* (k + 1) / 2    0 1 3 6 10
16     {
17       t += a1[k * (k + 1) / 2 + j];
18       ++k;                                      // j=0 i=1 a[0]+a[1]+a[3]+a[6]....=a[..+1]
19                                                 // j=1 i=2 a[1+1]+a[3+1]+a[6+1]....=a[..+2]
20     }
21     if ( a1[k * (k + 1) / 2 + i] != t )
22       return 0;
23     ++j;
24   }
25   return 1;
26 }

可以看作[0]---[k-1]行的[j]列求和   等于  [k]行的 [i] 

 

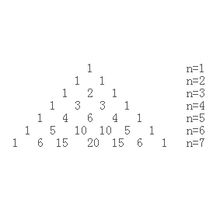
其实两个check就是在验证杨辉三角，

用到的特性(https://baike.baidu.com/item/%E6%9D%A8%E8%BE%89%E4%B8%89%E8%A7%92/215098?fr=aladdin)：

 

 

 

  1. 第n行数字的和为2^（n-1）。1=2^（1-1），1+1=2^（2-1），1+2+1=2^（3-1），1+3+3+1=2^（4-1），1+4+6+4+1=2^（5-1），1+5+10+10+5+1=2^（6-1）。
  2. 斜线上数字的和等于其向左（从左上方到右下方的斜线）或向右拐弯（从右上方到左下方的斜线），拐角上的数字。1+1=2，1+1+1=3，1+1+1+1=4，1+2=3，1+2+3=6，1+2+3+4=10，1+3=4，1+3+6=10，1+4=5

 

 

 

 

wp:

 1 def triangles():
 2     N=[1]
 3     while True:
 4         yield N
 5         N.append(0)
 6         N=[N[i-1] + N[i] for i in range(len(N))]
 7 n=0
 8 x=''
 9 for t in triangles():
10     # print(t)
11     x+=''.join(map(str,t))
12     n=n+1
13     if n == 20:
14         break
15 import hashlib
16 m=hashlib.md5(x.encode()).hexdigest()
17 # print(x)
18 print('RCTF{'+m+'}')

RCTF{37894beff1c632010dd6d524aa9604db}

 

posted @ 2019-09-04 22:23  DirWangK  阅读(533)  评论(0)  编辑  收藏  举报