TSP问题

TSP问题

问题简述：最短回路求解，也就是说一个人从现有的路线中选择可以走的路线，使得他经过了n个地点后，返回到出发地，其中，需要注意的是可以重复经过地点，也就是说只要求路上用的时间最短，但是不要求每个地点必须只经过一次。那么这个问题的解决方法可以是贪心法，遗传算法。蚁群算法以及模拟退火算法。具体如下图所示：

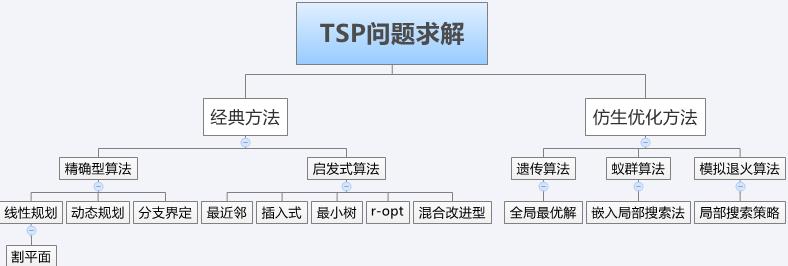
简单分为以下两种：

独立于问题的经典优化算法：

• 贪婪算法：             自顶向下，逐步迭代，简单迅速，但是容易得到局部最优解
• 模拟退火算法（SA）：  全局优化，求解速度快，加入随机状态，以概率选择的方式逼近最优状态。
• 遗传算法（GA）：      智能全局搜索，主要由编码、个体适应度评估和遗传运算三部分组成。
• 粒子群算法：（ACO）： 寻求优化路径的机率型算法，模拟进化，鲁棒性强，并行的分布式算法容易实现。

启发式搜索算法：2-opt、3-opt和Lin Kernighan（LK）等

• 回溯法
• 最近邻算法：

本文主要了解了关于遗传算法，蚁群算法和贪心法

 

1.遗传算法程序实现的步骤以及其中涉及到的计算公式

2.遗传算法参数的选取：迭代次数，初始的种子数量以及最终的交叉率和变异率，关于这些参数的选取需要具体问题具体分析。群体越大得到的结果越接近真实值，但是要考虑计算速度的问题，另外就是交叉率是用来控制种群的分布不要过于分散，使其集中于局部解周围，而变异率是用来控制种群的分布不要过于集中，使其均匀分散在解空间。

 群体大小，一般取20~100；终止进化代数，一般取100~500；交叉概率，一般取0.4~0.99；变异概率，一般取0.0001~0.1。

程序：

 

3.蚁群算法的程序步骤以及数学模型建立

 

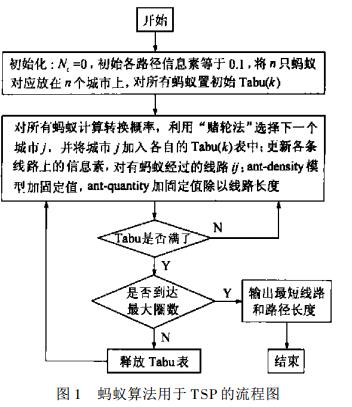
4.蚁群算法参数的选取：

• 蚁群个数：有的文献讲需要是城市个数的1.5倍，有的是城市个数的2-3倍
• 信息素重要程度Alpha：反映了蚂蚁在行走过程中堆积的信息素在指引道路上发挥的作用程度，Alpha过小的话会陷入局部最优，过小的话会导致信息素浓度高的正反馈增强，算法早熟收敛。[1,4]
• 启发式因子重要程度Beta：启发式信息在指引蚂蚁行走过程中的重要性，相当于我们的创新性发展，Beta过大会导致收敛速度加快，收敛性能降低，过小会导致简单随机搜索，很难找到最优解。[3,4.5]
• 信息素增强系数Q：功能使得算法能够充分利用好全局信息素反馈信息，以合理的收敛速度达到全局最优解。Q越大，算法的收敛能力越强，信息素的积累能力强，蚂蚁可以更快的得到信息素正反馈信息，Q<1000时，信息素强度 Q 越大，算法的收敛速度越快，但是对蚁群算法的整体求解效果有限；Q>7000时蚁群算法的收敛速度明显提高，但此时算法的全局搜索能力变差了，很容易陷入局部最优。
• 信息素蒸发系数Rpo：表征指引蚂蚁行走的信息素的残留程度，会影响到算法的收敛速度和全局收敛性；如果该值比较小的话需要迭代次数增加，所以在该值为0.5左右的时候可以得到较好的结果

5.贪心算法：

贪心算法：指的是只选择当前看来最好的选择，不一定能够得到最优解，但是可以得到局部最优解。贪心策略必须具备无后效性，也就是说，某个状态以后的过程只与当前状态有关，不会影响到以前的状态。

1、贪心算法的基本思路

从问题的某一个初始解触发逐步逼近给定的目标，以尽可能快地求得更好的解。当达到某算法中的某一步不能再继续前进时，算法停止。大致步骤如下：

1）建立数学模型来描述问题；
2）把求解的问题分成若干个子问题
3）对每一个子问题求解，得到子问题的局部最优解
4）把子问题的局部最优解合成原问题的一个解

2、贪心算法的实现框架

贪心算法没有固定的算法框架，算法设计的关键是贪心策略的选择，而贪心策略适用的前提是：局部最优策略能导致产生全局最优解。

    从问题的某一初始解出发；
    while （能朝给定总目标前进一步）
    { 
          利用可行的决策，求出可行解的一个解元素；
    }
    由所有解元素组合成问题的一个可行解；

3、贪心算法存在的问题

1）不能保证求得的最后解是最佳的；
2）不能用来求最大最小解问题；

4. 贪心策略的选择

在当前结点处遍历可以选择的所有的下一个节点，选择路程最短的作为下一个节点，将当前节点标记为已经经过的节点；然后再以选中的下一个节点为当前节点重复以上过程。

 

——————————————————————————

另外有趣的是看到别人的博客中提到的一种 很简单的解决方案，是先初始化一条路线，然后按照这条路线计算耗时长度，随机选择其中的两个点做交换即可得到新的路线，在计算用时长度，如果用时大于初始的路线，这替换掉原来的初始路线，否则仍然保持原来的不变，只要随机的次数足够大，就一定可以得到最想要的那个最短的路线长度。interesting