线性反馈移位寄存器(LFSR)-非线性反馈移位寄存器的verilog实现(产生伪随机数)
一、线性反馈移位寄存器(LFSR)
通过对事先选定的种子做运算使得人工生成的伪随机序列的过程,在实际中,随机种子的选择决定了输出的伪随机序列的不同,也就是说随机种子的选择至关重要。
产生伪随机数的方法最常见的是利用一种线性反馈移位寄存器(LFSR),它是由n个D触发器和若干个异或门组成的,如下图:
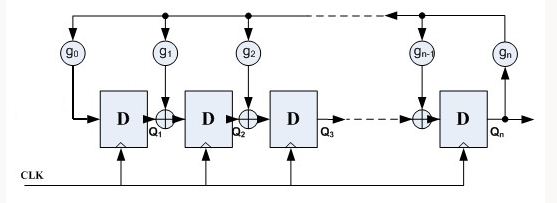
其中,gn为反馈系数,取值只能为0或1,取为0时表明不存在该反馈之路,取为1时表明存在该反馈之路;这里的反馈系数决定了产生随机数的算法的不同。用反馈函数表示成y=a0x^0+a1x+a2x^2.......反馈函数为线性的叫线性移位反馈序列,否则叫非线性反馈移位序列。
应该选取哪些位来进行异或才能保证最长周期为 ,这是一个很重要的问题。选取的“某些位”构成的序列叫做抽头序列,理论表明,要使LFSR得到最长的周期,这个抽头序列构成的多项式加1必须是一个本原多项式,也就是说这个多项式不可约,比如
,这是一个很重要的问题。选取的“某些位”构成的序列叫做抽头序列,理论表明,要使LFSR得到最长的周期,这个抽头序列构成的多项式加1必须是一个本原多项式,也就是说这个多项式不可约,比如 。
。
n个D触发器最多可以提供2^n-1个状态(不包括全0的状态),为了保证这些状态没有重复,gn的选择必须满足一定的条件。下面以n=3,g0=1,g1=1,g2=0,g3=1为例,说明LFSR的特性,具有该参数的LFSR结构如下图:
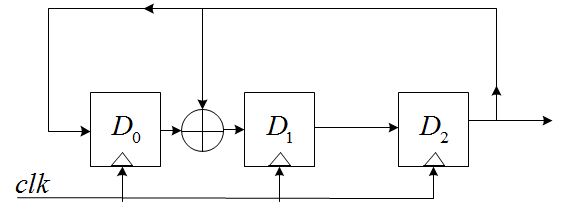
假设在开始时,D2D1D0=111(seed),那么,当时钟到来时,有:
D2=D1_OUT=1;
D1=D0_OUT^D2_OUT=0;
D0=D2_OUT=1;
即D2D1D0=101;同理,又一个时钟到来时,可得D2D1D0=001. ………………
画出状态转移图如下:
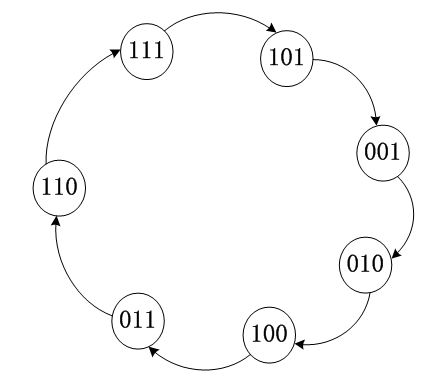
从图可以看出,正好有2^3-1=7个状态,不包括全0;
如果您理解了上图,至少可以得到三条结论:
1)初始状态是由SEED提供的;
2)当反馈系数不同时,得到的状态转移图也不同;必须保证gn===1,否则哪来的反馈?
3)D触发器的个数越多,产生的状态就越多,也就越“随机”;
verilog实现:
module RanGen( input rst_n, /*rst_n is necessary to prevet locking up*/ input clk, /*clock signal*/ input load, /*load seed to rand_num,active high */ input [7:0] seed, output reg [7:0] rand_num /*random number output*/ ); always@(posedge clk or negedge rst_n) begin if(!rst_n) rand_num <=8'b0; else if(load) rand_num <=seed; /*load the initial value when load is active*/ else begin rand_num[0] <= rand_num[7]; rand_num[1] <= rand_num[0]; rand_num[2] <= rand_num[1]; rand_num[3] <= rand_num[2]; rand_num[4] <= rand_num[3]^rand_num[7]; rand_num[5] <= rand_num[4]^rand_num[7]; rand_num[6] <= rand_num[5]^rand_num[7]; rand_num[7] <= rand_num[6]; end end endmodule
在通信系统的秘钥分析中需要用到LFSR作为保证密钥流得的周期长度,平衡性,而非线性组合函数决定了密钥流的密码性质,防止其被攻击。
二、非线性反馈移位寄存器
如下图,现在还没有太多的涉及到,所以只说些简单的概念:

posted on 2018-08-31 10:20 super_star123 阅读(14154) 评论(1) 收藏 举报


 浙公网安备 33010602011771号
浙公网安备 33010602011771号