FPGA开平方的实现
3种方法:
1.JPL近似的实现方法
`timescale 1ns / 1ps module complex_abs#(parameter N=32)( clk, syn_rst, dataa, datab, ampout); input clk; input [N-1:0] dataa; input [N-1:0] datab; input syn_rst; output reg [N-1:0]ampout; reg [N-1:0]dataa_reg ; reg [N-1:0]datab_reg ; wire [N-2:0]dataa_abs ; wire [N-2:0]datab_abs ; reg [N-2:0]dataabs_max,dataabs_min ; reg [N-1:0]absmin_3 ; always @(posedge clk) begin if(syn_rst == 1'b1) begin dataa_reg <= 'd0 ; datab_reg <= 'd0 ; end else begin dataa_reg <= dataa ; datab_reg <= datab ; end end assign dataa_abs = (dataa_reg[31] == 1'b1) ? (31'd0-dataa_reg[N-2:0]) : dataa_reg[N-2:0] ; assign datab_abs = (datab_reg[31] == 1'b1) ? (31'd0-datab_reg[N-2:0]) : datab_reg[N-2:0] ; always @(posedge clk) begin if(dataa_abs > datab_abs) begin dataabs_max <= dataa_abs ; dataabs_min <= datab_abs ; absmin_3 <= {1'b0,datab_abs}+{datab_abs,1'b0} ; end else begin dataabs_max <= datab_abs ; dataabs_min <= dataa_abs ; absmin_3 <= {1'b0,dataa_abs}+{dataa_abs,1'b0} ; end end always @(posedge clk) begin if(absmin_3 > {1'b0,dataabs_max}) ampout <= {1'b0,dataabs_max} - {4'b0,dataabs_max[N-2:3]} + {2'b0,dataabs_min[N-2:1]} ; else ampout <= {1'b0,dataabs_max} + {4'b0,dataabs_min[N-2:3]} ; end endmodule
2.调用IP模块的cordic算法实现效果
可选模式可以是fraction或者intergalactic
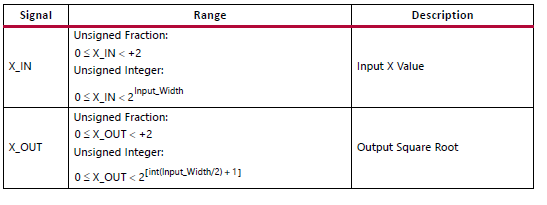
工程中输入数据的范围是远大于2的,于是我们可以采用实现方法是将所有的数据先归一化成-2~2之间,然后再进一步的采用cordic模块
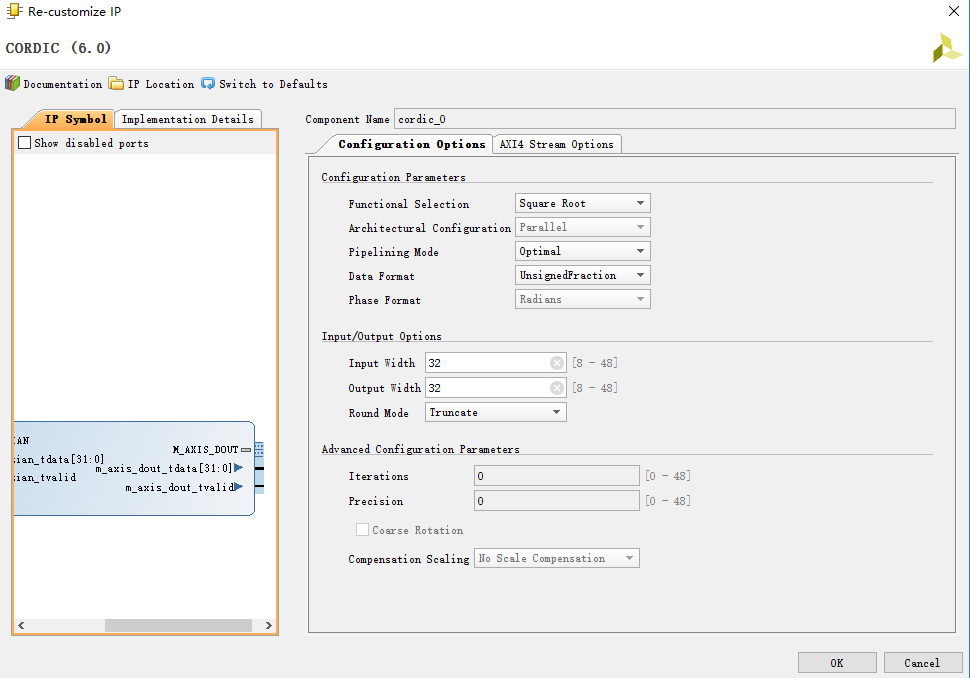
IP的配置如下
3.牛顿迭代忽略余数的实现方法
`timescale 1ns / 1ps ////////////////////////////////////////////////////////////////////////////////// // Company: // Engineer: // // Create Date: 2018/08/07 16:26:46 // Design Name: // Module Name: sqrt // Project Name: // Target Devices: // Tool Versions: // Description: // // Dependencies: // // Revision: // Revision 0.01 - File Created // Additional Comments: // ////////////////////////////////////////////////////////////////////////////////// module sqrt #( parameter d_width = 32, parameter q_width = d_width/2 - 1, parameter r_width = q_width + 1 ) ( input wire clk, input wire rst, input wire i_vaild, input wire [d_width-1:0] data_i,//data_21,data_12,data_22, //输入 output reg o_vaild, output reg [q_width:0] data_o, //输出 output reg [r_width:0] data_r //余数 ); //-------------------------------------------------------------------------------- reg [d_width-1:0] D [r_width:1]; //被开方数 reg [q_width:0] Q_z [r_width:1]; //临时 reg [q_width:0] Q_q [r_width:1]; //确认 reg ivalid_t [r_width:1]; //-------------------------------------------------------------------------------- always@(posedge clk or posedge rst) begin if(rst) begin D[r_width] <= 0; Q_z[r_width] <= 0; Q_q[r_width] <= 0; ivalid_t[r_width] <= 0; end else if(i_vaild) begin D[r_width] <= data_i;//data_11+data_21+data_12+data_22; //被开方数据 Q_z[r_width] <= {1'b1,{q_width{1'b0}}}; //实验值设置 Q_q[r_width] <= 0; //实际计算结果 ivalid_t[r_width] <= 1; end else begin D[r_width] <= 0; Q_z[r_width] <= 0; Q_q[r_width] <= 0; ivalid_t[r_width] <= 0; end end //------------------------------------------------------------------------------- // 迭代计算过程 //------------------------------------------------------------------------------- generate genvar i; for(i=r_width-1;i>=1;i=i-1) begin:U always@(posedge clk or posedge rst) begin if(rst) begin D[i] <= 0; Q_z[i] <= 0; Q_q[i] <= 0; ivalid_t[i] <= 0; end else if(ivalid_t[i+1]) begin if(Q_z[i+1]*Q_z[i+1] > D[i+1]) begin Q_z[i] <= {Q_q[i+1][q_width:i],1'b1,{{i-1}{1'b0}}}; Q_q[i] <= Q_q[i+1]; end else begin Q_z[i] <= {Q_z[i+1][q_width:i],1'b1,{{i-1}{1'b0}}}; Q_q[i] <= Q_z[i+1]; end D[i] <= D[i+1]; ivalid_t[i] <= 1; end else begin ivalid_t[i] <= 0; D[i] <= 0; Q_q[i] <= 0; Q_z[i] <= 0; end end end endgenerate //-------------------------------------------------------------------------------- // 计算余数与最终平方根 //-------------------------------------------------------------------------------- always@(posedge clk or posedge rst) begin if(rst) begin data_o <= 0; data_r <= 0; o_vaild <= 0; end else if(ivalid_t[1]) begin if(Q_z[1]*Q_z[1] > D[1]) begin data_o <= Q_q[1]; data_r <= D[1] - Q_q[1]*Q_q[1]; o_vaild <= 1; end else begin data_o <= {Q_q[1][q_width:1],Q_z[1][0]}; data_r <= D[1] - {Q_q[1][q_width:1],Q_z[1][0]}*{Q_q[1][q_width:1],Q_z[1][0]}; o_vaild <= 1; end end else begin data_o <= 0; data_r <= 0; o_vaild <= 0; end end //-------------------------------------------------------------------------------- endmodule
三种方法的精度对比以及资源占用情况
JPL近似

IPcordic使用:

牛顿迭代

可以看出资源占用:newtoon>JPL > IPcordic,精度的估计JPL<newtoon<IPcordic,
其中JPL 的计算速度快,但是误差太高了
单独求倒数的模块 / 快速高精度求平方根倒数的算法
posted on 2018-08-16 16:03 super_star123 阅读(10766) 评论(0) 收藏 举报

 浙公网安备 33010602011771号
浙公网安备 33010602011771号