08_GAN_double_moon
生成式对抗网络 (Generative Adversarial Networks)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import torch
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# 这是一个展示数据的函数
def plot_data(ax, X, Y, color = 'bone'):
plt.axis('off')
ax.scatter(X[:, 0], X[:, 1], s=1, c=Y, cmap=color)
借助于 sklearn.datasets.make_moons 库,生成双半月形的数据,同时把数据点画出来。
可以看出,数据散点呈现两个半月形状。
X, y = make_moons(n_samples=2000, noise=0.05)
n_samples = X.shape[0]
Y = np.ones(n_samples)
fig, ax = plt.subplots(1, 1, facecolor='#4B6EA9')
plot_data(ax, X, Y)
plt.show()

一个简单的 GAN
生成器和判别器的结构都非常简单,具体如下:
生成器: 32 ==> 128 ==> 2 判别器: 2 ==> 128 ==> 1 生成器生成的是样本,即一组坐标(x,y),我们希望生成器能够由一组任意的 32组噪声生成座标(x,y)处于两个半月形状上。
判别器输入的是一组座标(x,y),最后一层是sigmoid函数,是一个范围在(0,1)间的数,即样本为真或者假的置信度。如果输入的是真样本,得到的结果尽量接近1;如果输入的是假样本,得到的结果尽量接近0。
import torch.nn as nn
z_dim = 32
hidden_dim = 128
#定义生成器
net_G = nn.Sequential(
nn.Linear(z_dim , hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim,2))
#定义判别器
net_D = nn.Sequential(
nn.Linear(2,hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim,1),
nn.Sigmoid())
# 网络放到 GPU 上
net_G = net_G.to(device)
net_D = net_D.to(device)
# 定义网络的优化器
optimizer_G = torch.optim.Adam(net_G.parameters(),lr=0.0001)
optimizer_D = torch.optim.Adam(net_D.parameters(),lr=0.0001)
下面为对抗训练的过程:
batch_size = 50
nb_epochs = 1000
loss_D_epoch = []
loss_G_epoch = []
for e in range(nb_epochs):
np.random.shuffle(X)
real_samples = torch.from_numpy(X).type(torch.FloatTensor)
loss_G = 0
loss_D = 0
for t, real_batch in enumerate(real_samples.split(batch_size)):
# 固定生成器G,改进判别器D
# 使用normal_()函数生成一组随机噪声,输入G得到一组样本
z = torch.empty(batch_size,z_dim).normal_().to(device)
fake_batch = net_G(z)
# 将真、假样本分别输入判别器,得到结果
D_scores_on_real = net_D(real_batch.to(device))
D_scores_on_fake = net_D(fake_batch)
# 优化过程中,假样本的score会越来越小,真样本的score会越来越大,下面 loss 的定义刚好符合这一规律,
# 要保证loss越来越小,真样本的score前面要加负号
# 要保证loss越来越小,假样本的score前面是正号(负负得正)
loss = -torch.mean(torch.log(1-D_scores_on_fake) + torch.log(D_scores_on_real))
# 梯度清零
optimizer_D.zero_grad()
# 反向传播优化
loss.backward()
# 更新全部参数
optimizer_D.step()
loss_D += loss
# 固定判别器,改进生成器
# 生成一组随机噪声,输入生成器得到一组假样本
z = torch.empty(batch_size,z_dim).normal_().to(device)
fake_batch = net_G(z)
# 假样本输入判别器得到 score
D_scores_on_fake = net_D(fake_batch)
# 我们希望假样本能够骗过生成器,得到较高的分数,下面的 loss 定义也符合这一规律
# 要保证 loss 越来越小,假样本的前面要加负号
loss = -torch.mean(torch.log(D_scores_on_fake))
optimizer_G.zero_grad()
loss.backward()
optimizer_G.step()
loss_G += loss
if e % 50 ==0:
print(f'\n Epoch {e} , D loss: {loss_D}, G loss: {loss_G}')
loss_D_epoch.append(loss_D)
loss_G_epoch.append(loss_G)
Epoch 0 , D loss: 56.755985260009766, G loss: 31.247453689575195
Epoch 50 , D loss: 54.699317932128906, G loss: 29.562366485595703
Epoch 100 , D loss: 53.91822814941406, G loss: 28.176292419433594
Epoch 150 , D loss: 53.08674240112305, G loss: 27.95374298095703
Epoch 200 , D loss: 50.51228332519531, G loss: 29.543210983276367
Epoch 250 , D loss: 50.7359619140625, G loss: 29.252708435058594
Epoch 300 , D loss: 53.74419403076172, G loss: 28.915340423583984
Epoch 350 , D loss: 54.152130126953125, G loss: 33.3064079284668
Epoch 400 , D loss: 54.90654373168945, G loss: 26.523265838623047
Epoch 450 , D loss: 53.367496490478516, G loss: 34.682010650634766
Epoch 500 , D loss: 55.935176849365234, G loss: 25.24538230895996
Epoch 550 , D loss: 55.915977478027344, G loss: 31.561960220336914
Epoch 600 , D loss: 51.55472946166992, G loss: 32.71846389770508
Epoch 650 , D loss: 56.22766876220703, G loss: 24.23963737487793
Epoch 700 , D loss: 49.659446716308594, G loss: 27.562183380126953
Epoch 750 , D loss: 47.86740493774414, G loss: 28.97980499267578
Epoch 800 , D loss: 47.91128921508789, G loss: 29.37699317932129
Epoch 850 , D loss: 50.29985427856445, G loss: 27.83837127685547
Epoch 900 , D loss: 53.73185729980469, G loss: 27.47956085205078
Epoch 950 , D loss: 53.10669708251953, G loss: 32.23074722290039
显示 loss 的变化情况:
plt.plot(loss_D_epoch)
plt.plot(loss_G_epoch)
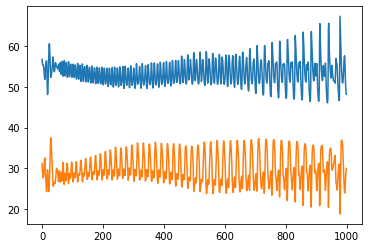
利用生成器生成一组假样本,观察是否符合两个半月形状的数据分布:
z = torch.empty(n_samples,z_dim).normal_().to(device)
fake_samples = net_G(z)
fake_data = fake_samples.cpu().data.numpy()
fig, ax = plt.subplots(1, 1, facecolor='#4B6EA9')
all_data = np.concatenate((X,fake_data),axis=0)
Y2 = np.concatenate((np.ones(n_samples),np.zeros(n_samples)))
plot_data(ax, all_data, Y2)
plt.show()

其中,白色的是原来的真实样本,黑色的点是生成器生成的样本。
看起来,效果是不令人满意的。现在把学习率修改为 0.001,batch_size改大到250,再试一次:
# 定义网络的优化器
optimizer_G = torch.optim.Adam(net_G.parameters(),lr=0.001)
optimizer_D = torch.optim.Adam(net_D.parameters(),lr=0.001)
batch_size = 250
loss_D_epoch = []
loss_G_epoch = []
for e in range(nb_epochs):
np.random.shuffle(X)
real_samples = torch.from_numpy(X).type(torch.FloatTensor)
loss_G = 0
loss_D = 0
for t, real_batch in enumerate(real_samples.split(batch_size)):
# 固定生成器G,改进判别器D
# 使用normal_()函数生成一组随机噪声,输入G得到一组样本
z = torch.empty(batch_size,z_dim).normal_().to(device)
fake_batch = net_G(z)
# 将真、假样本分别输入判别器,得到结果
D_scores_on_real = net_D(real_batch.to(device))
D_scores_on_fake = net_D(fake_batch)
# 优化过程中,假样本的score会越来越小,真样本的score会越来越大,下面 loss 的定义刚好符合这一规律,
# 要保证loss越来越小,真样本的score前面要加负号
# 要保证loss越来越小,假样本的score前面是正号(负负得正)
loss = -torch.mean(torch.log(1-D_scores_on_fake) + torch.log(D_scores_on_real))
# 梯度清零
optimizer_D.zero_grad()
# 反向传播优化
loss.backward()
# 更新全部参数
optimizer_D.step()
loss_D += loss
# 固定判别器,改进生成器
# 生成一组随机噪声,输入生成器得到一组假样本
z = torch.empty(batch_size,z_dim).normal_().to(device)
fake_batch = net_G(z)
# 假样本输入判别器得到 score
D_scores_on_fake = net_D(fake_batch)
# 我们希望假样本能够骗过生成器,得到较高的分数,下面的 loss 定义也符合这一规律
# 要保证 loss 越来越小,假样本的前面要加负号
loss = -torch.mean(torch.log(D_scores_on_fake))
optimizer_G.zero_grad()
loss.backward()
optimizer_G.step()
loss_G += loss
if e % 50 ==0:
print(f'\n Epoch {e} , D loss: {loss_D}, G loss: {loss_G}')
loss_D_epoch.append(loss_D)
loss_G_epoch.append(loss_G)
Epoch 0 , D loss: 8.75554084777832, G loss: 7.259755611419678
Epoch 50 , D loss: 10.344388008117676, G loss: 7.240558624267578
Epoch 100 , D loss: 11.16689395904541, G loss: 6.920253276824951
Epoch 150 , D loss: 11.00655460357666, G loss: 5.303454875946045
Epoch 200 , D loss: 9.425509452819824, G loss: 6.961507320404053
Epoch 250 , D loss: 9.168994903564453, G loss: 6.767005920410156
Epoch 300 , D loss: 10.260116577148438, G loss: 8.618905067443848
Epoch 350 , D loss: 9.377771377563477, G loss: 7.248937606811523
Epoch 400 , D loss: 9.875764846801758, G loss: 6.6888227462768555
Epoch 450 , D loss: 11.444906234741211, G loss: 6.769672393798828
Epoch 500 , D loss: 10.458311080932617, G loss: 5.506790637969971
Epoch 550 , D loss: 9.636507987976074, G loss: 6.657134532928467
Epoch 600 , D loss: 9.928154945373535, G loss: 7.593188285827637
Epoch 650 , D loss: 10.96129322052002, G loss: 7.4569315910339355
Epoch 700 , D loss: 10.582127571105957, G loss: 5.888792037963867
Epoch 750 , D loss: 9.59968376159668, G loss: 6.870519638061523
Epoch 800 , D loss: 10.376473426818848, G loss: 6.498831272125244
Epoch 850 , D loss: 10.90378475189209, G loss: 5.754330158233643
Epoch 900 , D loss: 10.771576881408691, G loss: 5.769700050354004
Epoch 950 , D loss: 10.896147727966309, G loss: 5.742316722869873
loss 明显减小了,我们再次利用噪声生成一组数据观察一下:
z = torch.empty(n_samples,z_dim).normal_().to(device)
fake_samples = net_G(z)
fake_data = fake_samples.cpu().data.numpy()
fig, ax = plt.subplots(1, 1, facecolor='#4B6EA9')
all_data = np.concatenate((X,fake_data),axis=0)
Y2 = np.concatenate((np.ones(n_samples),np.zeros(n_samples)))
plot_data(ax, all_data, Y2)
plt.show()

看得出来,随着batch size 的增大, loss 的降低,效果明显改善了~ (_)
下面我们生成更多的样本观察一下,结果也是非常有趣。
z = torch.empty(10*n_samples,z_dim).normal_().to(device)
fake_samples = net_G(z)
fake_data = fake_samples.cpu().data.numpy()
fig, ax = plt.subplots(1, 1, facecolor='#4B6EA9')
all_data = np.concatenate((X,fake_data),axis=0)
Y2 = np.concatenate((np.ones(n_samples),np.zeros(10*n_samples)))
plot_data(ax, all_data, Y2)
plt.show();




 浙公网安备 33010602011771号
浙公网安备 33010602011771号