floyd骚操作——传递闭包

传递闭包的含义指通过传递性推导出尽量多的元素之间的关系，而传递闭包一般都是采用floyd算法。

下面用两道题来实现传递闭包：

Problem 1（POJ3660）：

题目链接：http://poj.org/problem?id=3660

题目：

题意：n头牛参加比赛，给你m对关系（譬如给你a和b，那么给的就是a必赢b，当然，b能赢c，那么a也能赢c），问能确定多少头牛的排名。

思路：首先我们用flod算法将所有的关系进行传递，只要u能胜v，那么我们就将d[u][v]设为1，最后如果两者之间有d[u][v]=1或d[v][u]且二者不能同时出现时ans++。

代码实现如下：

#include <set>
#include <map>
#include <queue>
#include <stack>
#include <cmath>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long ll;
typedef pair<ll, ll> pll;
typedef pair<int, ll> pil;;
typedef pair<int, int> pii;
typedef unsigned long long ull;

#define lson i<<1
#define rson i<<1|1
#define bug printf("*********\n");
#define FIN freopen("D://code//in.txt", "r", stdin);
#define debug(x) cout<<"["<<x<<"]" <<endl;
#define IO ios::sync_with_stdio(false),cin.tie(0);

const double eps = 1e-8;
const int mod = 10007;
const int maxn = 4500 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f;

int n, m, u, v;
int relationship[107][107];

int main() {
    //FIN;
    scanf("%d%d", &n, &m);
    memset(relationship, 0, sizeof(relationship));
    for(int i = 1; i <= m; i++) {
        scanf("%d%d", &u, &v);
        relationship[u][v] = 1;
    }
    for(int k = 1; k <= n; k++) {
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= n; j++) {
                if(relationship[i][k] && relationship[k][j]) {
                    relationship[i][j] = 1;
                }
            }
        }
    }
    int ans = 0, j;
    for(int i = 1; i <= n; i++) {
        for(j = 1; j <= n; j++) {
            if(i == j) continue;
            if(relationship[i][j] == 0 && relationship[j][i] == 0) {
                break;
            }
        }
        if(j > n) ans++;
    }
    printf("%d\n", ans);
    return 0;
}

 

Problem 2（POJ1094）

题目链接：http://poj.org/problem?id=1094

题目：

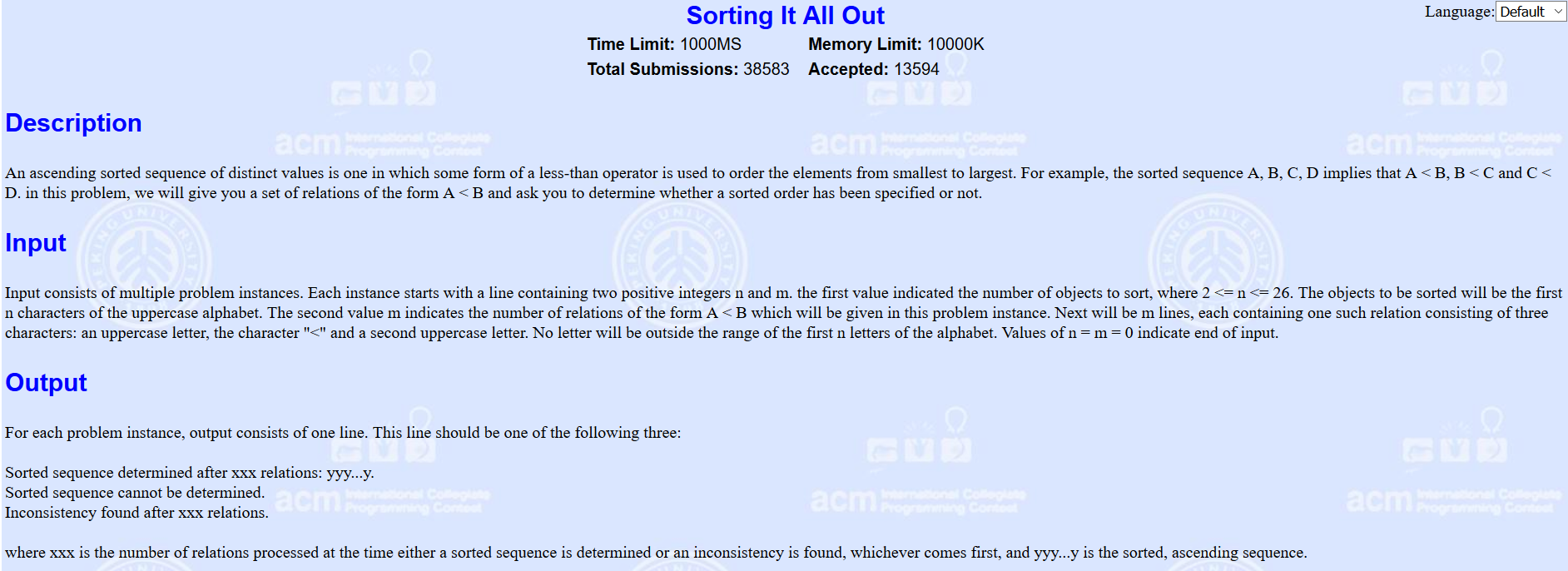
题意：给你n个大写字母，m对大小关系，根据他给的关系推测是否有大小矛盾的情况。如果有矛盾的就输出是在第几组关系时矛盾；如果不矛盾，判断只需要前t对组关系就能推测出他们从小到大的排序；如果没有以上两种情况就输入无法确定。

思路：对于每输入一对关系就跑一次floyd判断一遍，如果能推测出他们的关系，那么就跑一边拓扑排序求出他们从小打到的排序情况；如果有矛盾的关系就直接输出是在第几组关系时矛盾；如果没有以上情况就输出无法确定。

代码实现如下：

#include <set>
#include <map>
#include <queue>
#include <stack>
#include <cmath>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long ll;
typedef pair<ll, ll> pll;
typedef pair<int, ll> pil;;
typedef pair<int, int> pii;
typedef unsigned long long ull;

#define lson i<<1
#define rson i<<1|1
#define bug printf("*********\n");
#define FIN freopen("D://code//in.txt", "r", stdin);
#define debug(x) cout<<"["<<x<<"]" <<endl;
#define IO ios::sync_with_stdio(false),cin.tie(0);

const double eps = 1e-8;
const int mod = 10007;
const int maxn = 4500 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f;

int n, m, t, flag;
char s[1007][5];
int d[30][30], in[30], num[30];
vector<int> G[30];

bool floyd() {
    for(int k = 1; k <= n; k++) {
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= n; j++) {
                if(d[i][k] && d[k][j]) {
                    d[i][j] = 1;
                }
            }
        }
    }
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            if(i == j) continue;
            if((d[i][j] && d[j][i]) || (d[i][j] == 0 && d[j][i] == 0)) {
                return false;
            }
        }
    }
    return true;
}

void topsort(int m) {
    t = 0;
    for(int i = 1; i <= n; i++) {
        G[i].clear();
    }
    memset(in, 0, sizeof(in));
    for(int i = 1; i <= m; i++) {
        int x = s[i][0] - 'A' + 1, y = s[i][2] - 'A' + 1;
        G[x].push_back(y);
        in[y]++;
    }
    queue<int> q;
    for(int i = 1; i <= n; i++) {
        if(in[i] == 0) {
            q.push(i);
        }
    }
    while(!q.empty()) {
        int x = q.front(); q.pop();
        num[t++] = x;
        for(int i = 0; i < G[x].size(); i++) {
            int v = G[x][i];
            in[v]--;
            if(in[v] == 0) {
                q.push(v);
            }
        }
    }
}

int main() {
    //FIN;
    while(~scanf("%d%d", &n, &m)) {
        if(n == 0 && m == 0) break;
        memset(d, 0, sizeof(d));
        for(int i = 1; i <= m; i++) {
            scanf("%s", s[i]);
        }
        flag = 0;
        for(int i = 1; i <= m; i++) {
            int x = s[i][0] - 'A' + 1, y = s[i][2] - 'A' + 1;
            d[x][y] = 1;
            if(floyd()) {
                printf("Sorted sequence determined after %d relations: ", i);
                topsort(i);
                for(int i = 0; i < t; i++) {
                    printf("%c", num[i] - 1 + 'A');
                }
                printf(".\n");
                flag = 1;
            } else {
                for(int j = 1; j <= n; j++) {
                    for(int k = 1; k <= n; k++) {
                        if(j == k) continue;
                        if((d[j][k] && d[k][j])) {
                            printf("Inconsistency found after %d relations.\n", i);
                            flag = 1;
                            break;
                        }
                    }
                    if(flag) break;
                }
            }
            if(flag) break;
        }
        if(!flag) printf("Sorted sequence cannot be determined.\n");
    }
    return 0;
}