Educational Codeforces Round 47 (Rated for Div. 2) 题解

题目链接：http://codeforces.com/contest/1009

A. Game Shopping 题目：

题意：有n件物品，你又m个钱包，每件物品的价格为ai，每个钱包里的前为bi。你站在第一件物品前，如果你的第一个钱包能购买这件物品，你第一个钱包的钱直接消失（就相当于你是用第一个钱包里的所有钱购买了这件物品，不会找钱），如果无法购买那么就跳到下一件物品，以此类推，问你总共能购买多少件物品。

思路：直接模拟即可。

代码如下：

#include <bits/stdc++.h>
using namespace std;

const int maxn = 1007;
int n, m, ans;
int a[maxn], b[maxn];

int main() {
    cin >>n >>m;
    for(int i = 0; i < n; i++) {
        cin >>a[i];
    }
    for(int i = 0; i < m; i++) {
        cin >>b[i];
    }
    for(int i = 0, j = 0; i < n ; i++) {
        if(j >= m) break;
        if(b[j] >= a[i]) {
            j++;
            ans++;
        }
    }
    cout <<ans <<endl;
    return 0;
}

 

B. Minimum Ternary String  题目：

题意：给你一个只含012的串，0可以和1交换，1可以和2交换，0不可以和2交换，问进行多次交换后字典序最小的串是啥。

思路：因为1可以和02交换，所以要想字典序最小1必须全在2前面；2不能和0换，所以2和0的相对位置不变。故此题的思路就是将第一个2前的的所有0放在最前面，然后紧跟所有的1，后面的2和0就按照原顺序即可。方法1：暴力。方法2：借用vetctor。

代码如下：

//方法一
//#include <bits/stdc++.h>
//using namespace std;
//
//const int maxn = 1e5 + 7;
//int a[maxn];
//string s, t;
//
//int main() {
//    cin >>s;
//    int cnt1 = 0, cnt2 = 0, cnt3 = 0;
//    int pos = -1;
//    for(int i = 0; i <s.size(); i++) {
//        if(s[i] != '0') {
//            pos = i;
//            break;
//        }
//    }
//    for(int i = s.size() - 1; i >= pos; i--) {
//        if(s[i] == '0') {
//            cnt1++;
//            if(cnt3 > 0) {
//                for(int j = 0; j < cnt3; j++) {
//                    t += '2';
//                }
//                cnt3 = 0;
//            }
//        } else if(s[i] == '1') {
//            cnt2++;
//        } else if(s[i] == '2') {
//            cnt3++;
//            if(cnt1 > 0) {
//                for(int j = 0; j <cnt1; j++) {
//                    t += '0';
//                }
//                cnt1 = 0;
//            }
//        }
//    }
//    for(int i = 0; i < cnt3; i++) {
//        t += '2';
//    }
//    for(int i = 0; i <cnt2; i++) {
//        t += '1';
//    }
//    for(int i = 0; i < pos; i++) {
//        t += '0';
//    }
//    for(int i = 0; i < cnt1; i++) {
//        t += '0';
//    }
//    reverse(t.begin(), t.end());
//    cout <<t <<endl;
//    return 0;
//}

//方法二
#include <bits/stdc++.h>
using namespace std;

string s;
vector<char> v;

int main() {
    cin >>s;
    int cnt = 0;
    for(int i = 0; i < s.size(); i++) {
        if(s[i] == '1') cnt++;
        else v.push_back(s[i]);
    }
    int flag = 0;
    for(int i = 0; i < v.size(); i++) {
        if(v[i] == '2' && !flag) {
            while(cnt--) {
                cout<<"1";
            }
            cout <<"2";
            flag = 1;
        } else {
            cout <<v[i];
        }
    }
    //可能没有0、1，所以要在这里输出一遍
    for(int i = 0; i <cnt; i++) {
        cout <<"1";
    }
    cout <<endl;
    return 0;
}

 

C. Annoying Present 题目：

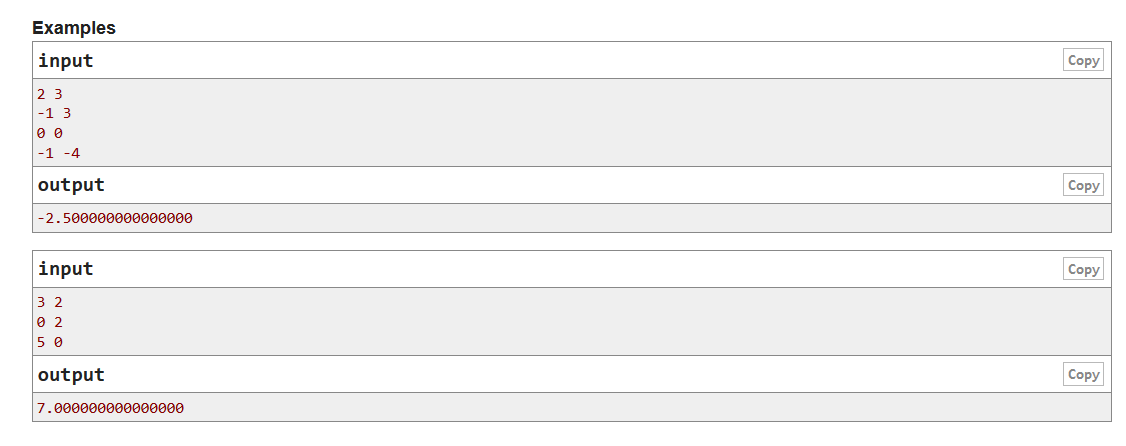
题意：有n个元素，初始为0，进行m次操作，每次操作给你x和d，你选择一个i，然后对每个元素（记为j，包括i）进行操作ai+x+d*dist(i,j)，问最后所有元素的最大平均值是多少。

思路：这个就是个贪心+公式题。这题的贪心方法是当d>0时，i选择最左（最右都可以，因为dist(i,j)是一样的，最后是算平均值，所有加在哪个元素上是没有区别的；当d<0时，选择最中间，此处要将n分奇偶，因为奇数和偶数是有所区别的。当推出这些之后会发现这题就是个等差数列求和，注意会爆int，比赛的时候就是被这个点坑死。ps.赛后这题是被hack人数最多的，本场hack数排第一的大佬就是这题hack了600多人，第一个坑点就是求和不能用double，会有精度损失，第二个坑点就是不要先除，要先求和再除。

代码实现如下：

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
ll n, m, x, d, ans;

int main() {
    scanf("%I64d%I64d", &n, &m);
    while(m--) {
        scanf("%I64d%I64d", &x, &d);
        ans += x * n;
        if(d > 0) {
            ans += (n - 1) * n / 2 * d;
        }  else {
            if(n & 1) ans += (n / 2 + 1) * (n / 2) * d;
            else ans += (n / 2) * (n / 2) * d;
        }
    }
    printf("%.8f\n", ans * 1.0 / n);
    return 0;
}

 

D. Relatively Prime Graph 题目：

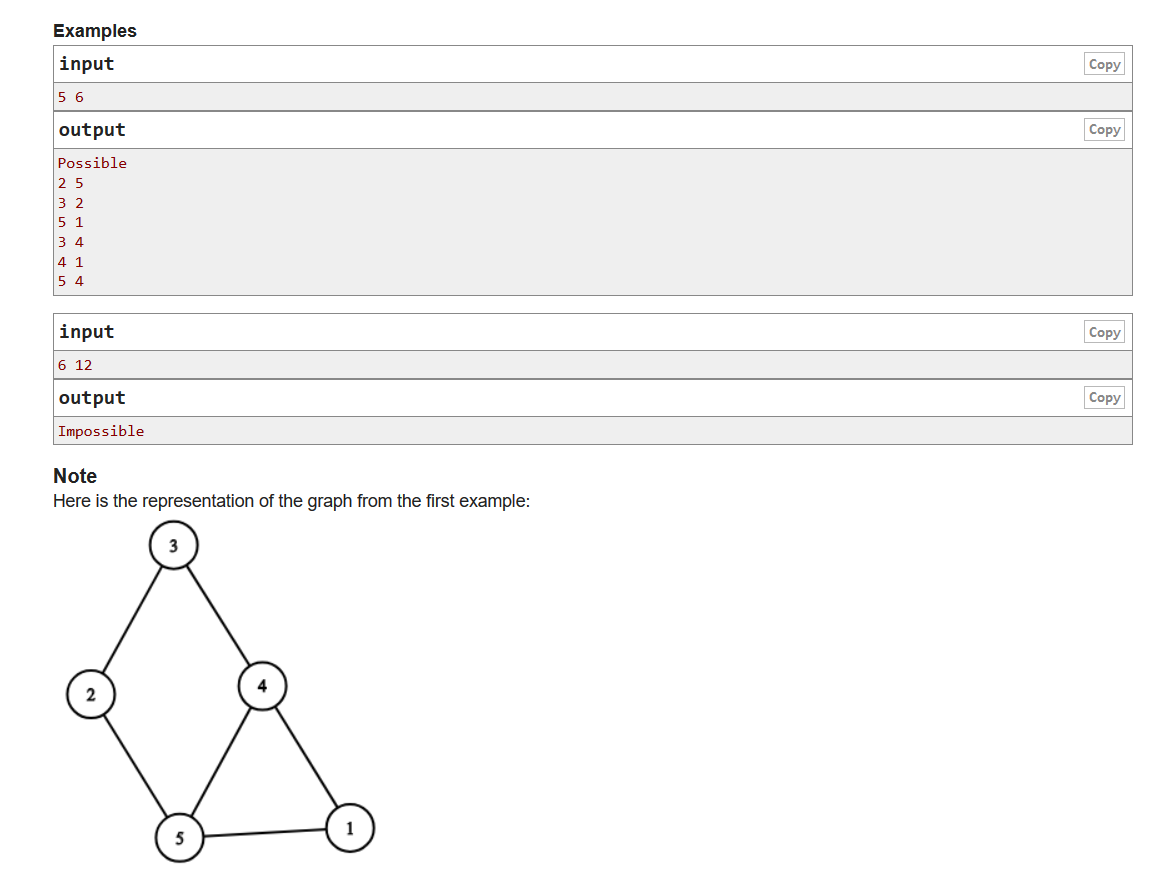
题意：构造一个只有n个点m条边的联通图，且相邻节点的编号要互质。

思路：当m<n-1时，由图联通知至少需要n-1条边，因此此处为impossible。1与所有的数都互质，所以此处保证了联通性。因为只需要m条边，由欧拉函数可以证得此题暴力的复杂度是稍大于O(m),我只会估算，具体证明暂时不会……因此此题可以暴力水过。

代码如下：

#include <cmath>
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

const int maxn = 1e5 + 7;
int n, m, t;

struct node {
    int x, y;
}edge[maxn];

int main() {
    cin >>n >>m;
    if(n - 1 > m) {
        puts("Impossible");
        return 0;
    }
    int flag = 0;
    for(int i = 1; i <= n; i++) {
        for(int j = i + 1; j <= n; j++) {
            if( __gcd(i, j) == 1) {
                edge[t].x = i;
                edge[t].y = j;
                t++;
                if(t >= m) {
                    flag = 1;
                    break;
                }
            }
        }
        if(flag) break;
    }
    if(flag) {
        puts("Possible");
        for(int i = 0; i < m; i++) {
            cout <<edge[i].x <<" " <<edge[i].y <<endl;
        }
    } else {
        puts("Impossible");
    }
    return 0;
}

 

---

 

赛后补题

E. Intercity Travelling 题目：

题意：Leha从数轴的0到n，中间的整数点都有可能有休息点也可能没有休息点。当你连续坐k站时，每两站间的疲劳值为a1,a2……ak，如果第k站有休息点，那么你可以在此处休息，然后接下来的站点的疲劳值又从a1开始，否则继续为ak+1。题目给你n和ai，每个站点有休息点的概率都是1/2，问你期望值*2^(n-1)的值。

思路：我们知道从0到1的疲劳值一定为a1，1到2的疲劳值为a1(1/2),a2(1/2)，括号里面为概率，当1有休息点时为a1，否则为a2；2到3的疲劳值为a1(1/2),a2(1/4),a3(1/4)……以此类推得到下图：

然后将他们加起来乘以2^（n-1)即可。ps.别用cin,cout，会T9，别问我怎么知道的！

代码实现如下：

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int mod = 998244353;
const int maxn = 1e6 + 7;
int n;
ll ans;
ll a[maxn], p[maxn];

int main() {
    scanf("%d", &n);
    p[0] = 1;
    for(int i = 1; i <= n; i++) {
        p[i] = p[i-1] * 2 % mod;
    }
    for(int i = 1; i <= n; i++) {
        scanf("%I64d", &a[i]);
    }
    ans = a[n];
    for(int i = 1; i < n; i++) {
        ans = (ans + (a[i] * (p[n - i] + p[n - i - 1] * (n - i) % mod) % mod) % mod) % mod;
    }
    printf("%I64d\n", ans);
    return 0;
}