湘潭校赛——又见斐波那契（矩阵快速幂）

题目链接：https://www.nowcoder.com/acm/contest/105/G

思路：这题一看数据范围就知道是个矩阵快速幂，通过构造矩阵知我们需要的转移矩阵为下图形式，不过需要特判1然后输出的是n-1的结果哦，因为这个我本题WA了==！矩阵快速幂最难得就是构造矩阵，当矩阵构造出来之后基本上就好做了~

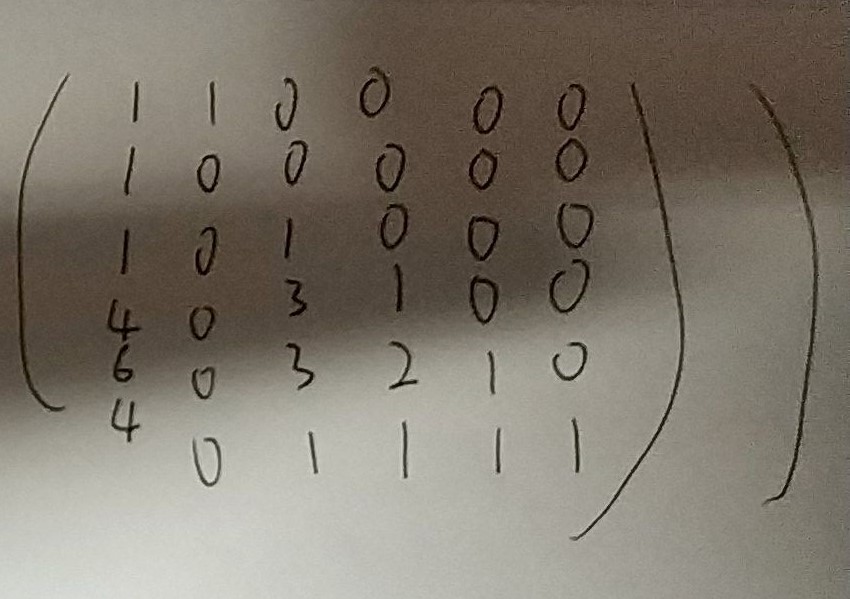
#include <cstdio>
#include <cstring>

typedef long long ll;
const int mod = 1e9 + 7;

int t;
ll n;

void mul(int f[6], int a[6][6]) {
    int c[6];
    memset(c, 0, sizeof(c));
    for(int i = 0; i < 6; i++) {
        for(int j = 0; j < 6; j++) {
            c[i] = (c[i] + (ll)f[j] * a[j][i] % mod) % mod;
        }
    }
    memcpy(f, c, sizeof(c));
}

void mulself(int a[6][6]) {
    int c[6][6];
    memset(c, 0, sizeof(c));
    for(int i = 0; i < 6; i++) {
        for(int j = 0; j < 6; j++) {
            for(int k = 0; k < 6; k++) {
                c[i][j] = (c[i][j] + (ll) a[i][k] * a[k][j] % mod) % mod;
            }
        }
    }
    memcpy(a, c, sizeof(c));
}

int main() {
    scanf("%d", &t);
    while(t--) {
        int f[6] = {1, 0, 1, 1, 1, 1};
        int a[6][6] = {{1, 1, 0, 0, 0, 0}, {1, 0, 0, 0, 0, 0}, {1, 0, 1, 0, 0, 0}, {4, 0, 3, 1, 0, 0}, {6, 0, 3, 2, 1, 0}, {4, 0, 1, 1, 1, 1}};
        scanf("%lld", &n);
        n = n - 1;
        for(; n; n >>= 1) {
            if(n & 1)
                mul(f, a);
            mulself(a);
        }
        printf("%d\n", f[0]);
    }
    return 0;
}

 

 

代码实现如下：