Gorgeous Sequence(HDU5360+线段树）

题目链接

传送门

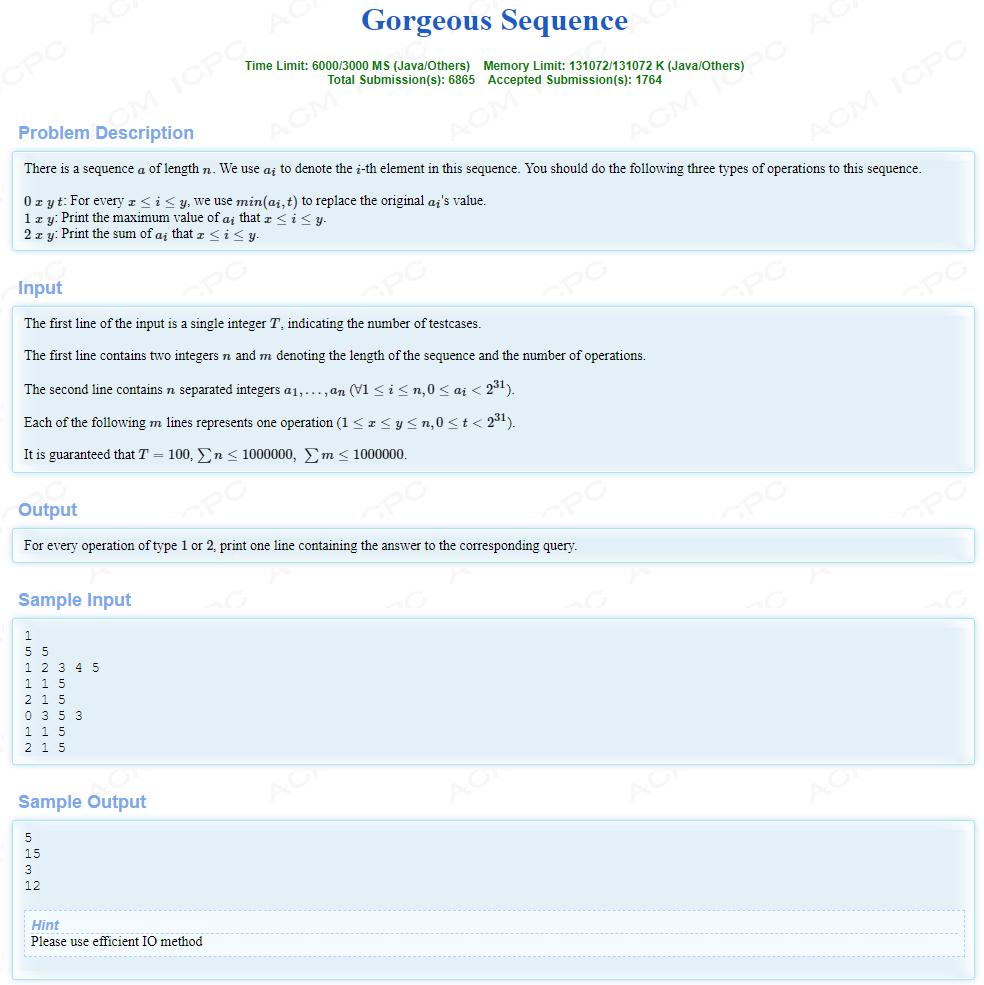
题面

思路

对于线段树的每个结点我们存这个区间的最大值\(mx\)、最大值个数\(cnt\)、严格第二大数\(se\)，操作\(0\)：

• 如果\(mx\leq val\)则不需要更新改区间；
• 如果\(se\leq val<mx\)则只需将区间最大值进行更新，此时\(sum=sum-cnt\times (mx - val)\)；
• 如果\(val<se\)则递归下去。
  (详情请看吉老师\(ppt\)
  因为一开始加了个\(lazy\)标记导致情况复杂化，且不好处理，对拍好久才发现。

代码实现如下

#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;

#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) x&(-x)
#define name2str(name) (#name)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]" <<endl
#define FIN freopen("D://Code//in.txt","r",stdin)
#define IO ios::sync_with_stdio(false),cin.tie(0)

const double eps = 1e-8;
const int mod = 1000000007;
const int maxn = 1000000 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3fLL;

int t, n, q, op, l, r, x;
int a[maxn];

struct node {
    int l, r, mx, se, cnt;
    LL sum;
}segtree[maxn<<2];

void push_up(int rt) {
    if(segtree[lson].mx >= segtree[rson].mx) {
        segtree[rt].mx = segtree[lson].mx;
        if(segtree[lson].mx == segtree[rson].mx) {
            segtree[rt].cnt = segtree[lson].cnt + segtree[rson].cnt;
            segtree[rt].se = max(segtree[lson].se, segtree[rson].se);
        } else {
            segtree[rt].cnt = segtree[lson].cnt;
            segtree[rt].se = max(segtree[lson].se, segtree[rson].mx);
        }
    } else {
        segtree[rt].mx = segtree[rson].mx;
        segtree[rt].cnt = segtree[rson].cnt;
        segtree[rt].se = max(segtree[lson].mx, segtree[rson].se);
    }
    segtree[rt].sum = segtree[lson].sum + segtree[rson].sum;
}

void push_down(int rt) {
    if(segtree[lson].mx > segtree[rt].mx) {
        segtree[lson].sum -= 1LL * segtree[lson].cnt * (segtree[lson].mx - segtree[rt].mx);
        segtree[lson].mx = segtree[rt].mx;
    }
    if(segtree[rson].mx > segtree[rt].mx) {
        segtree[rson].sum -= 1LL * segtree[rson].cnt * (segtree[rson].mx - segtree[rt].mx);
        segtree[rson].mx = segtree[rt].mx;
    }
}

void build(int rt, int l, int r) {
    segtree[rt].l = l, segtree[rt].r = r;
    segtree[rt].cnt = 0;
    segtree[rt].se = -inf;
    if(l == r) {
        scanf("%d", &segtree[rt].mx);
        segtree[rt].cnt = 1;
        segtree[rt].sum = segtree[rt].mx;
        return;
    }
    int mid = (l + r) >> 1;
    build(lson, l, mid);
    build(rson, mid + 1, r);
    push_up(rt);
}

void update(int rt, int l, int r, int x) {
    if(segtree[rt].l == segtree[rt].r) {
        if(x < segtree[rt].mx) {
            segtree[rt].mx = x;
            segtree[rt].sum = x;
        }
        return;
    }
    if(segtree[rt].mx <= x) {
        return;
    }
    if(segtree[rt].l == l && segtree[rt].r == r && segtree[rt].se < x) {
        segtree[rt].sum -= 1LL * segtree[rt].cnt * (segtree[rt].mx - x);
        segtree[rt].mx = x;
        return;
    }
    push_down(rt);
    int mid = (segtree[rt].l + segtree[rt].r) >> 1;
    if(r <= mid) update(lson, l, r, x);
    else if(l > mid) update(rson, l, r, x);
    else {
        update(lson, l, mid, x);
        update(rson, mid + 1, r, x);
    }
    push_up(rt);
}

int query1(int rt, int l, int r) {
    if(segtree[rt].l == l && segtree[rt].r == r) {
        return segtree[rt].mx;
    }
    push_down(rt);
    int mid = (segtree[rt].l + segtree[rt].r) >> 1;
    if(r <= mid) return query1(lson, l, r);
    else if(l > mid) return query1(rson, l, r);
    else return max(query1(lson, l, mid), query1(rson, mid + 1, r));
}

LL query2(int rt, int l, int r) {
    if(segtree[rt].l == l && segtree[rt].r == r) {
        return segtree[rt].sum;
    }
    push_down(rt);
    int mid = (segtree[rt].l + segtree[rt].r) >> 1;
    if(r <= mid) return query2(lson, l, r);
    else if(l > mid) return query2(rson, l, r);
    else return query2(lson, l, mid) + query2(rson, mid + 1, r);
}

int main() {
#ifndef ONLINE_JUDGE
    FIN;
#endif // ONLINE_JUDGE
    scanf("%d", &t);
    while(t--) {
        scanf("%d%d", &n, &q);
        build(1, 1, n);
        while(q--) {
            scanf("%d%d%d", &op, &l, &r);
            if(op == 0) {
                scanf("%d", &x);
                update(1, l, r, x);
            } else if(op == 1) {
                printf("%d\n", query1(1, l, r));
            } else {
                printf("%lld\n", query2(1, l, r));
            }
        }
    }
    return 0;
}

\(ps.\)在这里贴几组数据帮助大家找\(bug\)：

Input

4
3 3
1167335444 1577370753 1848018061
0 1 1 577330338
0 2 2 25842012
0 1 2 2081289238
13 4
2092509202 227315181 749615568 1128285623 1865077425 1779921231 1864459374 2072421312 1354378672 20493878 1571784125 1812319171 1767594153
0 1 5 1790650736
0 1 13 1584744642
2 8 8
2 1 1
5 5
206578960 2138572088 1531732505 476202306 1864171007
1 1 1
0 2 2 159050728
1 1 3
1 2 3
2 1 2
7 1
243178151 1437281627 1355768485 1346835035 87676247 1491584559 2023149422
1 4 6

Output

1584744642
1584744642
206578960
1531732505
1531732505
365629688
1491584559

Input

1
3 5
1281319710 961042073 1775161183
0 1 3 1126944798
1 3 3
2 1 2
1 1 1
0 2 2 339585676

Output

1126944798
2087986871
1126944798