The Shortest Statement(Educational Codeforces Round 51 (Rated for Div.2)+最短路+LCA+最小生成树)
题目链接
题面

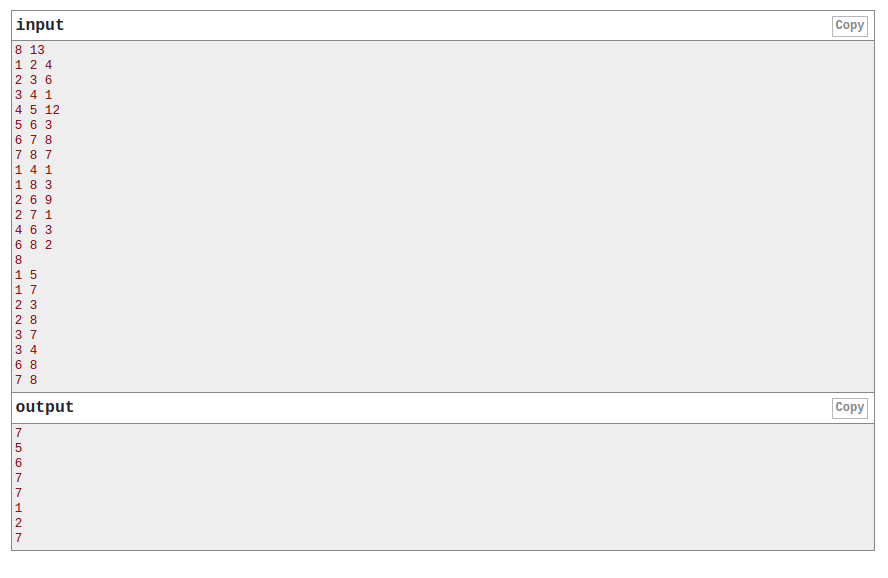
题意
给你一张有\(n\)个点\(m\)条边的联通图(其中\(m\leq n+20)\),\(q\)次查询,每次询问\(u\)与\(v\)之间的最短路。
思路
由于边数最多只比点数大21,因此我们可以先跑出一棵最小生成树,然后将非树上边的两个端点跑一边最短路,然后每次查询就比较\(max((dis[u]+dis[v]-2dis[lca(u,v)]),dist[i][u]+dis[i][v])\),其中\(dis[u]\)表示\(u\)到最小生成树根节点的距离,\(dist[i][u]\)表示第\(i\)个点到\(u\)的最短路,其中\(i\)为非树边的某个端点。
代码实现如下
#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> piL;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) x&(-x)
#define name2str(name) (#name)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]" <<endl
#define FIN freopen("in","r",stdin)
#define IO ios::sync_with_stdio(false),cin.tie(0)
const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 1e5 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3fLL;
int n, m, tot, u, v, q;
set<int> s;
set<int>::iterator it;
int fa[maxn], vis[maxn], head[maxn];
LL dis[45][maxn];
struct node {
int u, v, w;
bool operator < (const node& x) const {
return w < x.w;
}
}pp[maxn];
struct edge {
int v, w, next;
}ed[maxn<<1];
void init() {
tot = 0;
for(int i = 0; i <= n; i++) {
head[i] = -1;
fa[i] = i;
}
}
void add(int u, int v, int w) {
ed[tot].v = v;
ed[tot].w = w;
ed[tot].next = head[u];
head[u] = tot++;
}
struct LCA {
int tot;
int deep[maxn], fa[maxn][30], head[maxn];
LL cost[maxn];
struct edge {
int v, w, next;
}ed[maxn<<1];
void init() {
tot = 0;
for(int i = 0; i <= n; i++) {
head[i] = -1;
cost[i] = deep[i] = 0;
}
}
void add(int u, int v, int w) {
ed[tot].v = v;
ed[tot].w = w;
ed[tot].next = head[u];
head[u] = tot++;
}
void dfs(int u, int d, int p) {
deep[u] = d, fa[u][0] = p;
for(int i = head[u]; ~i; i = ed[i].next) {
int v = ed[i].v;
if(v == p) continue;
cost[v] = cost[u] + ed[i].w;
dfs(v, d + 1, u);
}
}
void lca() {
for(int i = 1; i <= n; i++) {
for(int j = 1; (1<<j) <= n; j++) {
fa[i][j] = -1;
}
}
for(int j = 1; (1<<j) <= n; j++) {
for(int i = 1; i <= n; i++) {
if(fa[i][j-1] != -1) {
fa[i][j] = fa[fa[i][j-1]][j-1];
}
}
}
}
int query(int u, int v) {
if(deep[u] <= deep[v]) swap(u, v);
int k;
for(k = 0; (1 << (1 + k)) <= deep[u]; k++);
for(int i = k; i >= 0; i--) {
if(deep[u] - (1<<i) >= deep[v]) {
u = fa[u][i];
}
}
if(u == v) return u;
for(int i = k; i >= 0; i--) {
if(fa[u][i] != -1 && fa[u][i] != fa[v][i]) {
u = fa[u][i], v = fa[v][i];
}
}
return fa[u][0];
}
LL dis(int u, int v) {
return cost[u] + cost[v] - 2 * cost[query(u, v)];
}
}L;
void dij(int s, int num) {
for(int i = 1; i <= n; ++i) {
dis[num][i] = INF, vis[i] = 0;
}
priority_queue<pLi, vector<pLi>, greater<pLi> > q;
dis[num][s] = 0;
q.push({0, s});
int u, v;
while(!q.empty()) {
u = q.top().second; q.pop();
if(vis[u]) continue;
vis[u] = 1;
for(int i = head[u]; ~i; i = ed[i].next) {
v = ed[i].v;
if(dis[num][v] > dis[num][u] + ed[i].w) {
dis[num][v] = dis[num][u] + ed[i].w;
q.push({dis[num][v], v});
}
}
}
}
int fi(int x) {
return fa[x] == x ? x : fa[x] = fi(fa[x]);
}
void kruskal() {
sort(pp + 1, pp + m + 1);
for(int i = 1; i <= m; ++i) {
int p1 = fi(pp[i].u), p2 = fi(pp[i].v);
if(p1 == p2) continue;
fa[p1] = p2;
vis[i] = 1;
}
}
int main() {
#ifndef ONLINE_JUDGE
FIN;
#endif
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; ++i) {
scanf("%d%d%d", &pp[i].u, &pp[i].v, &pp[i].w);
}
init();
kruskal();
L.init();
for(int i = 1; i <= m; ++i) {
if(vis[i]) L.add(pp[i].u, pp[i].v, pp[i].w), L.add(pp[i].v, pp[i].u, pp[i].w);
else s.insert(pp[i].u), s.insert(pp[i].v);
add(pp[i].u, pp[i].v, pp[i].w), add(pp[i].v, pp[i].u, pp[i].w);
}
L.dfs(1, 0, 0);
L.lca();
int num = 0;
for(it = s.begin(); it != s.end(); ++it) dij(*it, num++);
scanf("%d", &q);
while(q--) {
scanf("%d%d", &u, &v);
LL ans = L.dis(u, v);
for(int i = 0; i < num; ++i) {
ans = min(ans, dis[i][u] + dis[i][v]);
}
printf("%lld\n", ans);
}
return 0;
}
版权声明:本文允许转载,转载时请注明原博客链接,谢谢~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号