The Preliminary Contest for ICPC China Nanchang National Invitational and International Silk-Road Programming Contest
题目链接
A题
题面
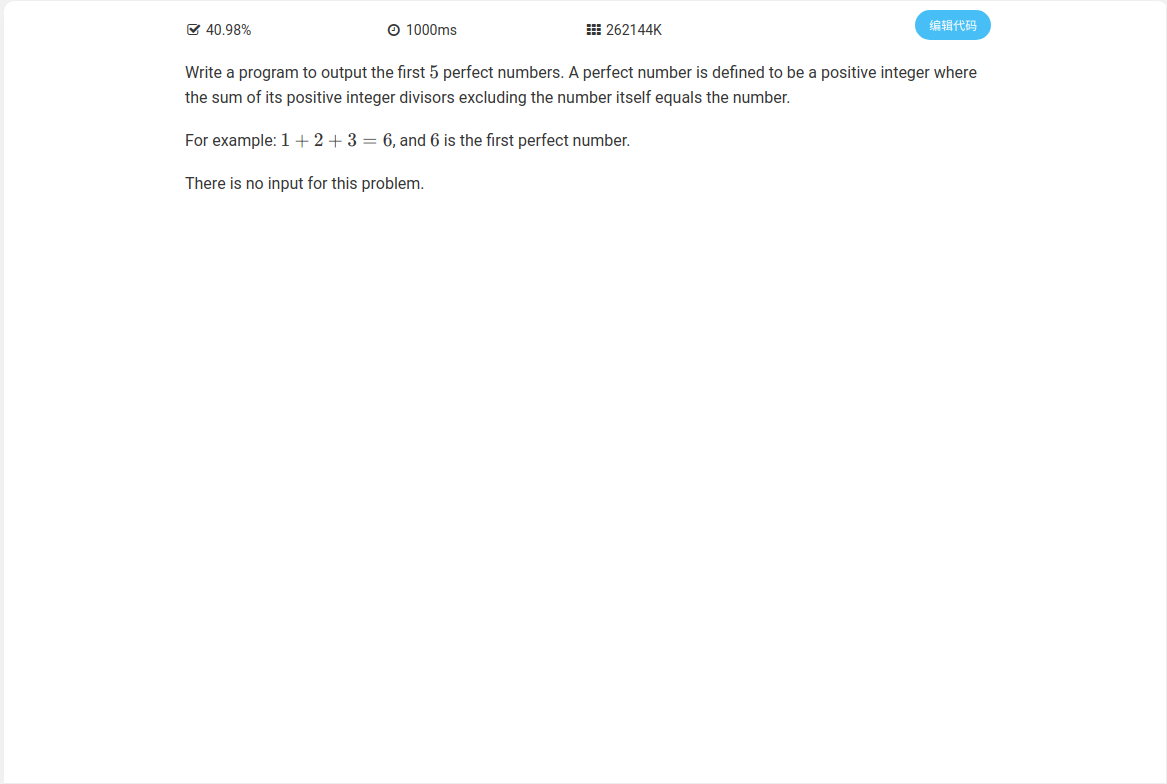
代码实现如下
#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> piL;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) x&(-x)
#define name2str(name) (#name)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]" <<endl
#define FIN freopen("in","r",stdin)
#define IO ios::sync_with_stdio(false),cin.tie(0)
const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 1e5 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3fLL;
int main() {
printf("6\n28\n496\n8128\n33550336\n");
return 0;
}
C题
题面

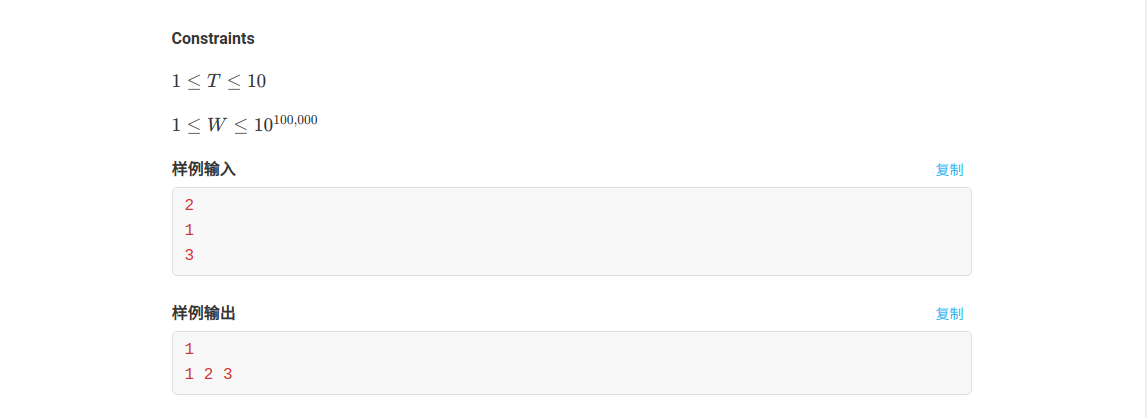
题意
定义\(F\)函数为斐波那契数列,给你一个\(W\),要你构造一个集合\(S\)使得集合内的元素\(f_i\)满足:
如果不满足输出\(-1\),否则输出字典序最小的一个集合。
思路
对于\(n\)很大的时候我们先将它一直减最大的小于等于\(n\)的斐波那契数,直到\(n\leq20\),然后用二进制来枚举选哪些斐波那契数来凑这个\(n\)。
今年湖南多校对抗赛第一场的一道题和这题很像,题解请戳这里。
对\(java\)和\(python\)不太熟悉,所以代码写的有点挫\(\dots\dots\)
\(java\)代码实现如下
import java.util.*;
import java.math.*;
public class Main {
static BigInteger pw[] = new BigInteger[40];
static BigInteger f[] = new BigInteger[3];
static BigInteger a[][] = new BigInteger[3][3];
public static void mul(BigInteger f[], BigInteger a[][]) {
BigInteger c[] = new BigInteger[3];
for(int i = 0; i < 2; ++i) c[i] = BigInteger.ZERO;
for(int i = 0; i < 2; ++i) {
for(int j = 0; j < 2; ++j) {
c[i] = c[i].add(f[j].multiply(a[j][i]));
}
}
for(int i = 0; i < 2; ++i) f[i] = c[i];
}
public static void mulself(BigInteger a[][]) {
BigInteger c[][] = new BigInteger[3][3];
for(int i = 0; i < 2; ++i) {
for(int j = 0; j < 2; ++j) {
c[i][j] = BigInteger.ZERO;
}
}
for(int i = 0; i < 2; ++i) {
for(int j = 0; j < 2; ++j) {
for(int k = 0; k < 2; ++k) {
c[i][j] = c[i][j].add(a[i][k].multiply(a[k][j]));
}
}
}
for(int i = 0; i < 2; ++i) {
for(int j = 0; j < 2; ++j) {
a[i][j] = c[i][j];
}
}
}
public static void init() {
pw[1] = BigInteger.ONE;
pw[2] = BigInteger.ONE;
for(int i = 3; i <= 30; ++i) {
pw[i] = pw[i-1].add(pw[i-2]);
}
for(int cnt = 1; cnt <= 30; ++cnt) {
if(cnt <= 4) {
if(cnt <= 3) pw[cnt] = BigInteger.ONE;
else pw[cnt] = BigInteger.valueOf(2);
continue;
}
f[0] = BigInteger.ONE;
f[1] = BigInteger.ONE;
a[0][0] = BigInteger.ONE; a[0][1] = BigInteger.ONE;
a[1][0] = BigInteger.ONE; a[1][1] = BigInteger.ZERO;
BigInteger x = pw[cnt];
x = x.subtract(BigInteger.valueOf(2));
while(x.compareTo(BigInteger.ZERO) > 0) {
if(x.mod(BigInteger.valueOf(2)).equals(BigInteger.ONE)) {
mul(f, a);
}
mulself(a);
x = x.divide(BigInteger.valueOf(2));
}
pw[cnt] = f[0];
}
}
public static void main(String[] args) {
init();
Vector<Integer> ans = new Vector<Integer>();
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
while(t-- != 0) {
BigInteger n = sc.nextBigInteger();
ans.clear();
int idx = 30, flag = 1;
while(true) {
if(n.compareTo(BigInteger.valueOf(20))<=0) break;
int p = -1;
for(int i = idx; i >= 1; --i) {
if(n.compareTo(pw[i]) >= 0) {
p = i;
break;
}
}
if(p == -1) {
flag = 0;
break;
}
n = n.subtract(pw[p]);
idx = p - 1;
ans.add(p);
if(n.equals(BigInteger.ZERO)) break;
}
if(flag == 0) {
System.out.println(-1);
} else {
if(n.equals(BigInteger.ZERO)) {
int vis = 0;
for(int i = ans.size() - 1; i >= 0; --i) {
if(vis == 1) System.out.print(" ");
vis = 1;
System.out.print(ans.elementAt(i));
}
System.out.println();
} else {
idx = 6;
int tot = 1<<idx, pp = 0;
for(int i = 1; i < tot; ++i) {
BigInteger nw = BigInteger.ZERO;
for(int j = 1; j <= idx; ++j) {
if((i & (1<<(j-1))) > 0) {
nw = nw.add(pw[j]);
}
}
if(n.equals(nw)) {
for(int j = idx; j >= 1; --j) {
if((i & (1<<(j-1))) > 0) {
ans.add(j);
}
}
pp = 1;
break;
}
}
if(pp == 0) System.out.println(-1);
else {
int vis = 0;
for(int i = ans.size() - 1; i >= 0; --i) {
if(vis == 1) System.out.print(" ");
vis = 1;
System.out.print(ans.elementAt(i));
}
System.out.println();
}
}
}
}
sc.close();
}
}
\(python\)代码实现如下
def __mul__(f, a):
c = [0] * 3
for i in range(2):
for j in range(2):
c[i] = c[i] + f[j] * a[j][i]
return c
def __mulself__(a):
c = [[0] * 3 for i in range(3)]
for i in range(2):
for j in range(2):
for k in range(2):
c[i][j] = c[i][j] + a[i][k] * a[k][j]
return c
pw = [0]*36
pw[1] = pw[2] = 1
for i in range(3, 31):
pw[i] = pw[i-1] + pw[i-2]
pw[3] = 1
pw[4] = 2
f = [0] * 3
a = [[0] * 3 for i in range(2)]
for i in range(5, 31):
x = pw[i]
x -= 2
f[0] = f[1] = 1
a[0][0] = a[0][1] = a[1][0] = 1
a[1][1] = 0
while(x > 0):
if(x & 1):
f = __mul__(f, a)
a = __mulself__(a)
x >>= 1
pw[i] = f[0]
T = eval(input())
for icase in range(T):
n = eval(input())
ans = []
idx = 30
flag = 1
while(True):
if(n <= 20):
break;
p = -1
for i in range(idx, 0, -1):
if(n >= pw[i]):
p = i
break
if(p == -1):
flag = 0
break
n -= pw[p]
idx = p - 1
ans.append(p)
if(n == 0):
break;
if(flag == 0):
print(-1)
else:
pp = False
if(n == 0):
pp = True
else:
idx = 6
tot = 1<<idx
pp = False
for i in range(1, tot):
nw = 0
for j in range(1, idx + 1):
if((i & (1<<(j-1))) > 0):
nw += pw[j]
if(n == nw):
for j in range(idx, 0, -1):
if ((i & (1 << (j - 1))) > 0):
ans.append(j)
pp = True
break
if(pp):
ans.sort()
for i in range(len(ans)):
print(ans[i], end="")
if(i != len(ans) - 1):
print(end=" ")
else:
print()
else:
print(-1)
H题
题面
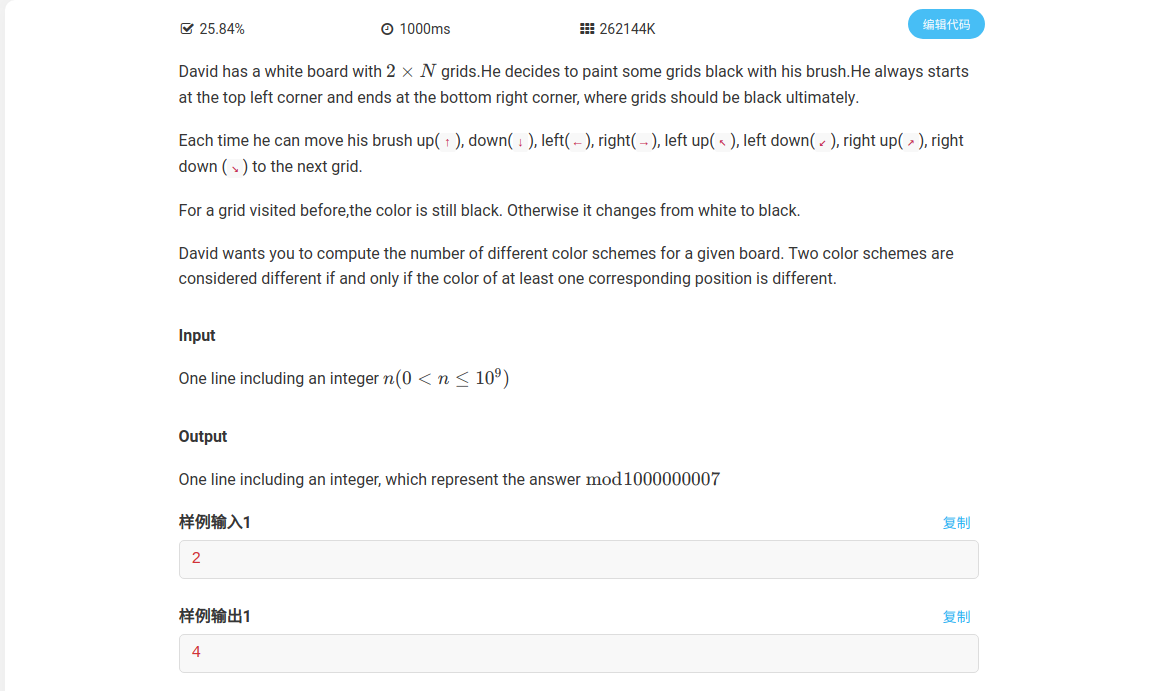
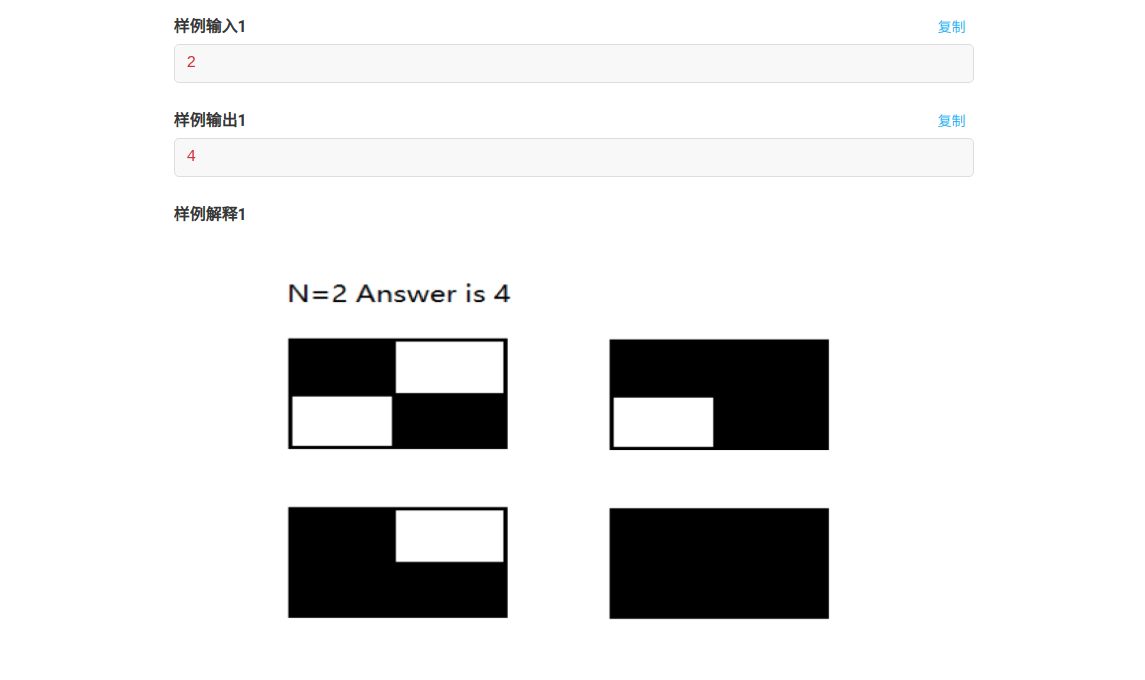
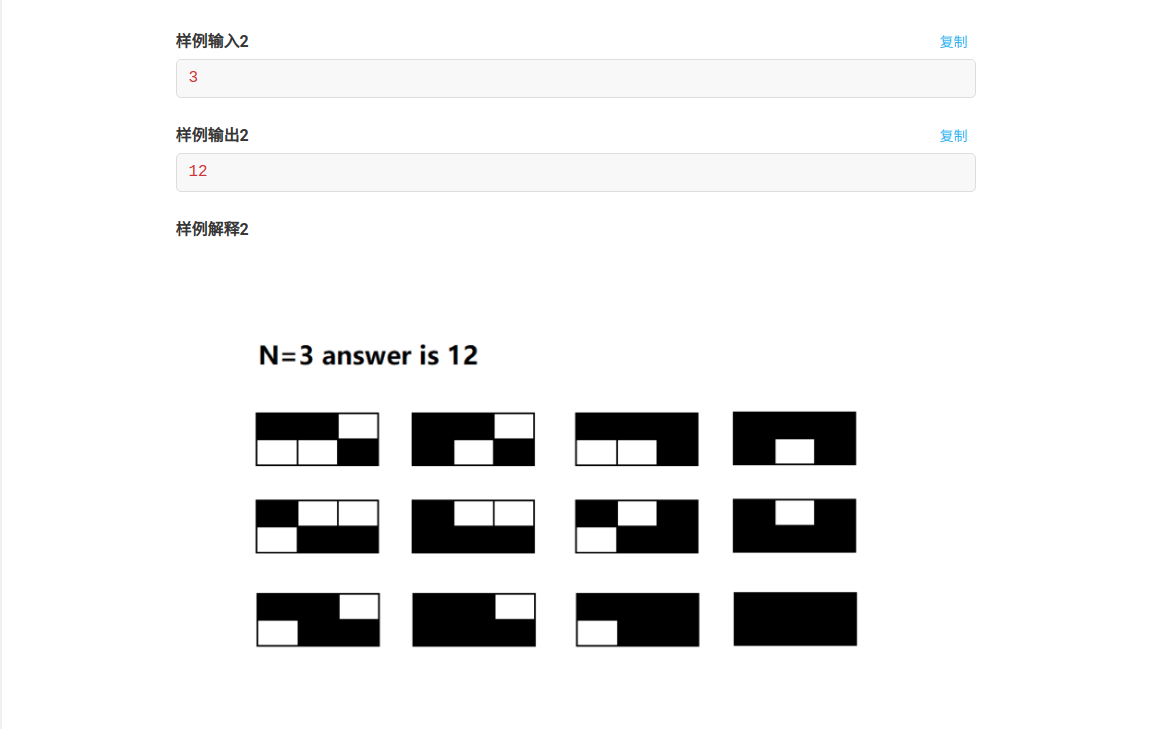
题意
给你一个\(2\times n\)的矩阵,你初始时在\((1,1)\)处,每次移动可以往周围八个方向移动,问你到达右下角的方案数是多少。
思路
我们假设前i-1列都已经求好了方案数,那么\(dp[i][j]\)表示第\(i\)列第\(j\)行的方案数,则\(dp[i][1]=dp[i-1][1]+dp[i-1][2],dp[i][2]=dp[i-1][1]+dp[i-1][2]+dp[i][1]\),因此\(dp[i][2]=2*(dp[i-1][1]+dp[i-1][2])=4\times 3^{i-2}\)。
代码实现如下
#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> piL;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) x&(-x)
#define name2str(name) (#name)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]" <<endl
#define FIN freopen("in","r",stdin)
#define IO ios::sync_with_stdio(false),cin.tie(0)
const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 1e5 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3fLL;
int n;
LL qpow(LL x, int n) {
LL res = 1;
while(n) {
if(n & 1) res = res * x % mod;
x = x * x % mod;
n >>= 1;
}
return res;
}
int main() {
scanf("%d", &n);
if(n == 1) return printf("1\n") * 0;
printf("%lld\n", 4LL * qpow(3, n - 2) % mod);
return 0;
}
I题
题面
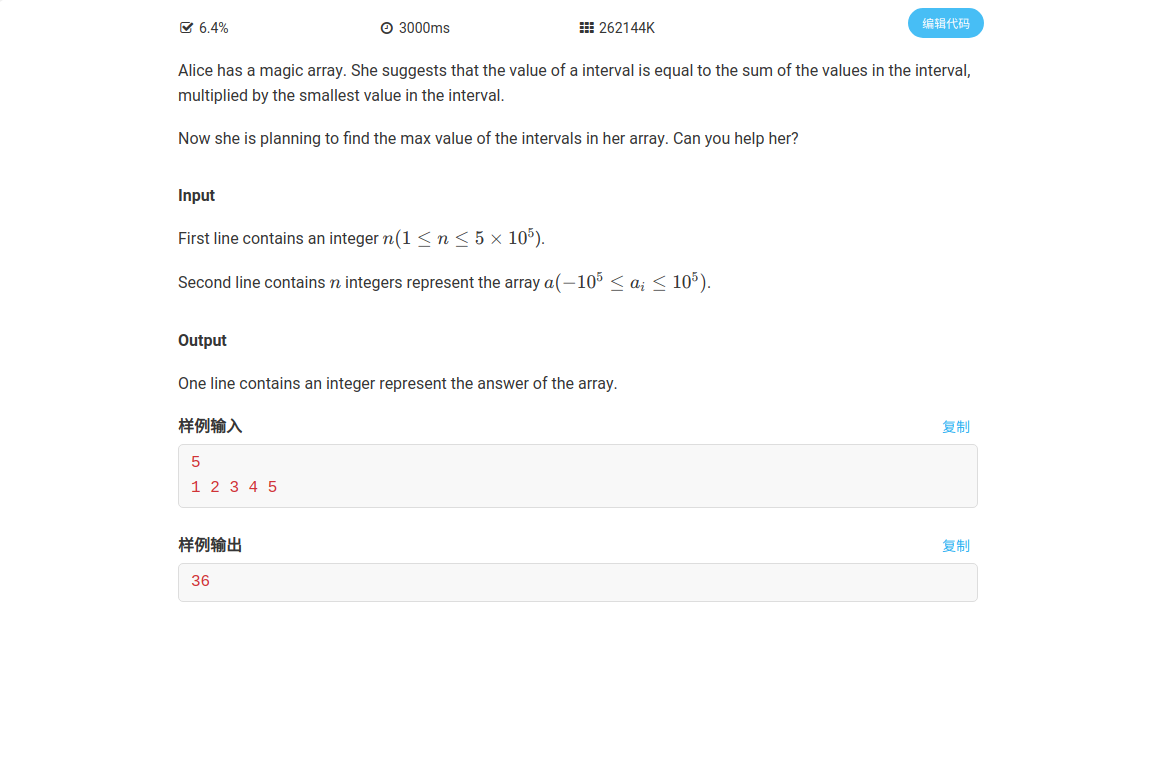
思路
我们先用单调栈来求出以\(a_i\)为区间最小值的左右端点,然后再用线段树来维护前\(i\)个前缀和的最大值和最小值,然后对于每个数进行查询即可。
代码实现如下
#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) x&(-x)
#define name2str(name) (#name)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]" <<endl
#define FIN freopen("D://code//in.txt","r",stdin)
#define IO ios::sync_with_stdio(false),cin.tie(0)
const double eps = 1e-8;
const int mod = 1000000007;
const int maxn = 5e5 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3fLL;
int n;
stack<int> s;
LL sum[maxn];
int a[maxn], l[maxn], r[maxn];
struct node {
int l, r;
LL mx, mn;
}segtree[maxn<<2];
void push_up(int rt) {
segtree[rt].mx = max(segtree[lson].mx, segtree[rson].mx);
segtree[rt].mn = min(segtree[lson].mn, segtree[rson].mn);
}
void build(int rt, int l, int r) {
segtree[rt].l = l, segtree[rt].r = r;
if(l == r) {
segtree[rt].mx = segtree[rt].mn = sum[l];
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid); build(rson, mid + 1, r);
push_up(rt);
}
LL query(int rt, int l, int r, int op) {
if(segtree[rt].l == l && segtree[rt].r == r) {
if(op == 1) return segtree[rt].mx;
else return segtree[rt].mn;
}
int mid = (segtree[rt].l + segtree[rt].r) >> 1;
if(r <= mid) return query(lson, l, r, op);
else if(l > mid) return query(rson, l, r, op);
else {
if(op == 1) return max(query(lson, l, mid, op), query(rson, mid + 1, r, op));
else return min(query(lson, l, mid, op), query(rson, mid + 1, r, op));
}
}
int main(){
#ifndef ONLINE_JUDGE
FIN;
#endif
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
l[i] = r[i] = i;
sum[i] = sum[i-1] + a[i];
}
for(int i = 1; i <= n; ++i) {
while(s.size() && a[s.top()] > a[i]) {
r[s.top()] = i - 1;
s.pop();
}
s.push(i);
}
while(s.size()) {
r[s.top()] = n;
s.pop();
}
for(int i = n; i >= 1; --i) {
while(s.size() && a[s.top()] > a[i]) {
l[s.top()] = i + 1;
s.pop();
}
s.push(i);
}
while(s.size()) {
l[s.top()] = 1;
s.pop();
}
build(1, 0, n);
LL ans = -INF, tmp;
for(int i = 1; i <= n; ++i) {
if(a[i] < 0) {
tmp = query(1, i, r[i], 2) - query(1, l[i] - 1, i, 1);
} else {
tmp = query(1, i, r[i], 1) - query(1, l[i]-1, i, 2);
}
ans = max(ans, tmp * a[i]);
}
printf("%lld\n", ans);
return 0;
}
J题
题面
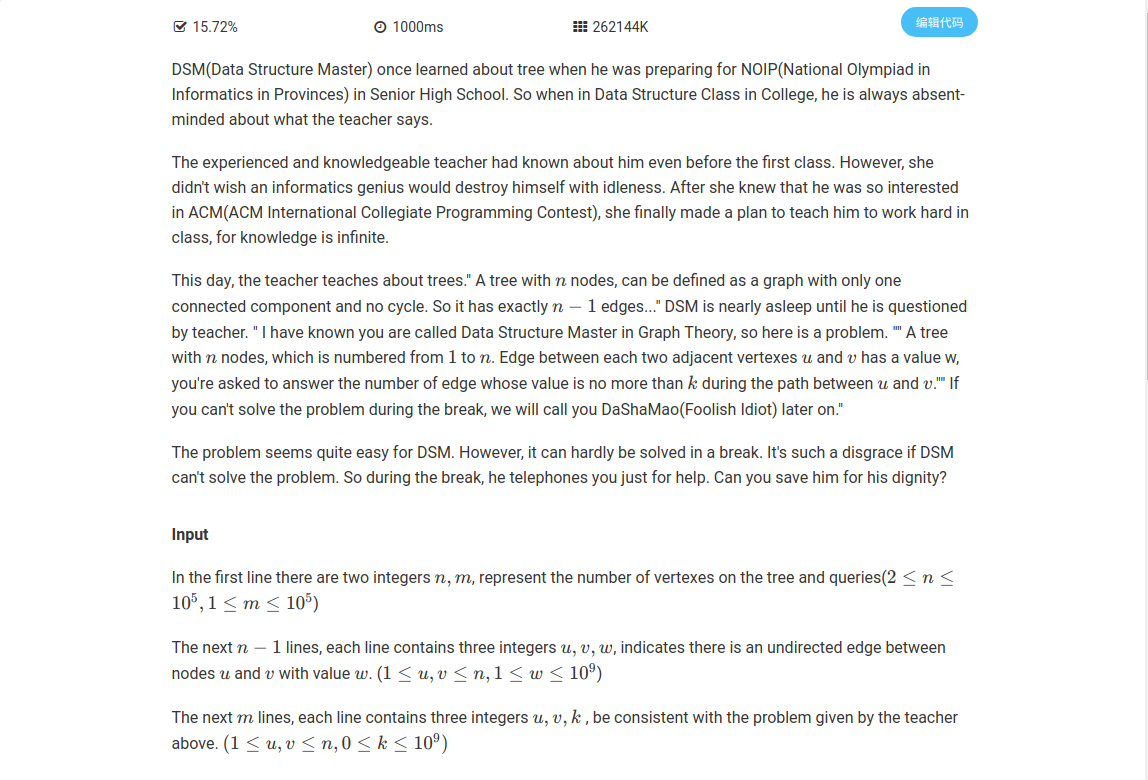


题意
给你一棵有\(n\)个结点的树,问你\(u,v\)之间所有的边权小于等于\(k\)的数量。
思路
主席树板子题。
代码实现如下
#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> piL;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) x&(-x)
#define name2str(name) (#name)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]" <<endl
#define FIN freopen("in","r",stdin)
#define IO ios::sync_with_stdio(false),cin.tie(0)
const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 1e5 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3fLL;
vector<int> v;
int n, q, x, y, w, len, cnt, tot;
int head[maxn], root[maxn], fa[maxn][30], deep[maxn];
struct edge {
int v, w, next;
}ed[maxn<<1];
void add(int u, int v, int w) {
ed[tot].v = v;
ed[tot].w = w;
ed[tot].next = head[u];
head[u] = tot++;
}
int getid(int x) {
return lower_bound(v.begin(), v.end(), x) - v.begin() + 1;
}
struct node {
int l, r, sum;
}tree[maxn*40];
void update(int l, int r, int& x, int y, int pos) {
tree[++cnt] = tree[y], tree[cnt].sum++, x = cnt;
if(l == r) return;
int mid = (l + r) >> 1;
if(mid >= pos) update(l, mid, tree[x].l, tree[y].l, pos);
else update(mid + 1, r, tree[x].r, tree[y].r, pos);
}
int query(int l, int r, int x, int y, int pos) {
if(r <= pos) return tree[y].sum - tree[x].sum;
if(l == r) return tree[y].sum - tree[x].sum;
int mid = (l + r) >> 1;
if(pos <= mid) return query(l, mid, tree[x].l, tree[y].l, pos);
else return tree[tree[y].l].sum - tree[tree[x].l].sum + query(mid + 1, r, tree[x].r, tree[y].r, pos);
}
void dfs(int u, int d, int p) {
deep[u] = d;
fa[u][0] = p;
for(int i = head[u]; ~i; i = ed[i].next) {
int v = ed[i].v;
if(v != p) {
update(1, len, root[v], root[u], getid(ed[i].w));
dfs(v, d + 1, u);
}
}
}
void lca() {
for(int i = 1; i <= n; i++) {
for(int j = 1; (1 << j) <= n; j++) {
fa[i][j] = -1;
}
}
for(int j = 1; (1 << j) <= n; j++) {
for(int i = 1; i <= n; i++) {
if(fa[i][j-1] != -1) {
fa[i][j] = fa[fa[i][j-1]][j-1];
}
}
}
}
int cal(int u, int v) {
if(deep[u] < deep[v]) swap(u, v);
int k;
for(k = 0; (1 << (1 + k)) <= deep[u]; k++);
for(int i = k; i >= 0; i--) {
if(deep[u] - (1 << i) >= deep[v]) {
u = fa[u][i];
}
}
if(u == v) return u;
for(int i = k; i >= 0; i--) {
if(fa[u][i] != -1 && fa[u][i] != fa[v][i]) {
u = fa[u][i];
v = fa[v][i];
}
}
return fa[u][0];
}
struct que {
int u, v, w;
}ask[maxn];
int main() {
scanf("%d%d", &n, &q);
for(int i = 1; i <= n; ++i) {
head[i] = -1;
}
for(int i = 1; i < n; ++i) {
scanf("%d%d%d", &x, &y, &w);
v.push_back(w);
add(x, y, w); add(y, x, w);
}
for(int i = 1; i <= q; ++i) {
scanf("%d%d%d", &ask[i].u, &ask[i].v, &ask[i].w);
v.push_back(ask[i].w);
}
sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
len = v.size();
dfs(1, 1, 0);
lca();
for(int i = 1; i <= q; ++i) {
int p = cal(ask[i].u, ask[i].v);
printf("%d\n", query(1, len, root[p], root[ask[i].u], getid(ask[i].w)) + query(1, len, root[p], root[ask[i].v], getid(ask[i].w)));
}
return 0;
}
K题
题面

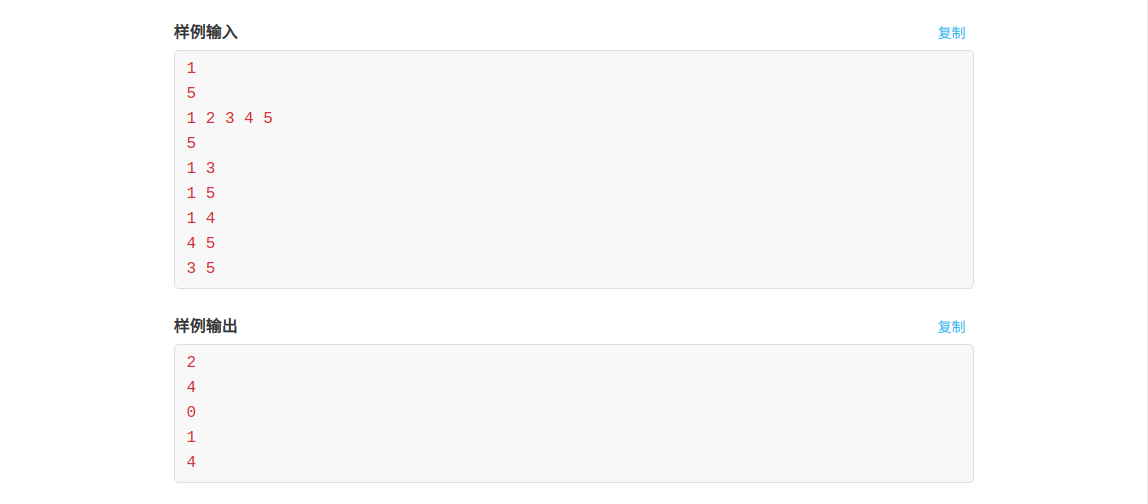
题意
首先定义一下函数:
\(f(l,r):\bigoplus a_i(l\leq i \leq r)\)
\(g(l,r):\bigoplus f(x,y)(l\leq x\leq y\leq r)\)
\(w(l,r):\bigoplus g(x,y)(l\leq x\leq y\leq r)\)
给你\(n\)个数,\(q\)次查询,每次查询\(l,r\)间的\(w(l,r)\)的值。
思路
打表找规律即可。
我们首先打表发现:
然后就可以用下述代码打出\(w(l,,r)\)的解,最后用前缀和预处理一下就行。
打表代码如下
#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> piL;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) x&(-x)
#define name2str(name) (#name)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]" <<endl
#define FIN freopen("in","r",stdin)
#define IO ios::sync_with_stdio(false),cin.tie(0)
const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 1e5 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3fLL;
map<int, int> mp;
int main() {
for(int i = 1; i <= 25; ++i) { //区间长度
mp.clear();
for(int j = 1; j <= i; j += 2) { //g的长度
for(int s = 1; s <= i; ++s) {
if(s + j - 1 > i) break;
for(int k = s; k <= i; k += 2) {
if(k + j - 1 > i) break;
mp[k] ++;
if(mp[k] % 2 == 0) mp[k] = 0;
}
}
}
printf("[%d]:", i);
for(int j = 1; j <= i; ++j) {
if(mp[j]) printf("%d ", j);
}
printf("\n");
}
return 0;
}
代码实现如下
#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> piL;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) x&(-x)
#define name2str(name) (#name)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]" <<endl
#define FIN freopen("in","r",stdin)
#define IO ios::sync_with_stdio(false),cin.tie(0)
const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 1e5 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3fLL;
int t, n, q;
int a[maxn];
int sum[4][maxn];
int main() {
scanf("%d", &t);
while(t--) {
scanf("%d", &n);
a[0] = 0;
memset(sum, 0, sizeof(sum));
for(int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
}
for(int i = 0; i < 4; ++i) {
sum[i][i] = a[i];
for(int j = i; j + 4 <= n; j += 4) {
sum[i][j+4] = sum[i][j] ^ a[j+4];
}
}
scanf("%d", &q);
int l, r;
while(q--) {
scanf("%d%d", &l, &r);
int len = r - l + 1;
if(len % 4 == 1) {
int num = l % 4;
int s = 0, t = r;
if(l >= 4) {
s = l - 4;
}
t = l + len / 4 * 4;
if(t > r) t -= 4;
printf("%d\n", sum[num][t] ^ sum[num][s]);
} else if(len % 4 == 3) {
int num = (l + 1) % 4;
int s = 0, t = r;
if(l >= 4) {
s = (l + 1) - 4;
}
t = (l + 1) + len / 4 * 4;
if(t > r) t -= 4;
printf("%d\n", sum[num][t] ^ sum[num][s]);
} else if(len % 4 == 0) {
printf("0\n");
} else {
int num1 = l % 4;
int s1 = 0, t1 = r;
if(l >= 4) {
s1 = l - 4;
}
t1 = l + len / 4 * 4;
if(t1 > r) t1 -= 4;
int num2 = (l + 1) % 4;
int s2 = 0, t2 = r;
if(l >= 4) {
s2 = (l + 1) - 4;
}
t2 = (l + 1) + len / 4 * 4;
if(t2 > r) t2 -= 4;
printf("%d\n", sum[num1][t1] ^ sum[num1][s1] ^ sum[num2][t2] ^ sum[num2][s2]);
}
}
}
return 0;
}
M题
题面
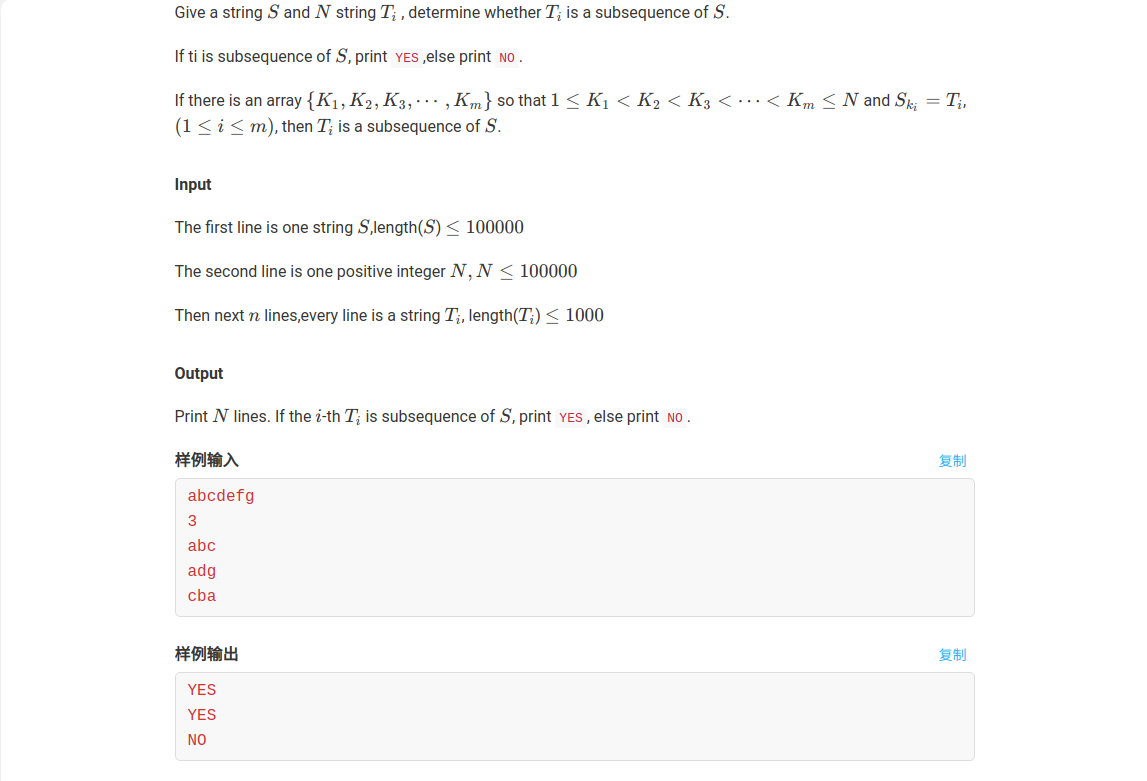
题意
给你一个字符串\(S\),然后\(q\)次查询,每次查询\(T\)串是否在\(S\)的子序列中出现过。
思路
由于这题数据比较水,因此我们可以用二分过,但是正解是序列自动机或者\(dp\)预处理。
二分代码实现如下
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 1e5 + 7;
char s[maxn], t[1010];
vector<int>v[30];
vector<int>::iterator it;
int main() {
scanf ( "%s", s + 1 );
int len = strlen ( s + 1 ), q, x, flag, len1, cnt, i;
for ( i = 1 ; i <= len ; i++ ) {
int x = s[i] - 'a';
v[x].push_back ( i );
}
scanf ( "%d", &q );
while ( q-- ) {
scanf ( "%s", t + 1 );
flag = 0;
len1 = strlen ( t + 1 );
if ( len1 > len ) {
printf ( "NO\n" );
continue;
}
x = t[1] - 'a';
if ( v[x].size() != 0 ) cnt = v[x][0];
else {
printf ( "NO\n" );
continue;
}
for ( i = 2 ; i <= len1 ; i++ ) {
x = t[i] - 'a';
if ( v[x].size() == 0 || v[x].back() <= cnt ) {
flag = 1;
break;
}
it = upper_bound ( v[x].begin(), v[x].end(), cnt );
if ( it == v[x].end() ) {
flag = 1;
break;
}
cnt = ( *it );
}
if ( flag ) printf ( "NO\n" );
else printf ( "YES\n" );
}
return 0;
}

