EM算法

EM算法

 

EM算法是一种迭代法，其目标是求解似然函数或后验概率的极值，而样本中具有无法观测的隐含变量。因为隐变量的存在，我们无法直接通过最大化似然函数来确定参数的值。可以采用一种策略，构造出对数似然函数的一个下界函数，这个函数不含有隐变量，然后优化这个下界。不断的提高这个下界，使原问题达到最优解，这就是EM算法所采用的思路。算法的构造依赖于Jensen不等式。

 

算法在实现时首先随机初始化参数 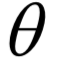       的值，接下来循环迭代，每次迭代时分为两步：

 

E步，基于当前的参数估计值 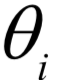，计算在给定x时对z的条件概率的数学期望：

 

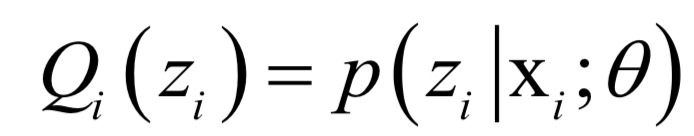
M步，求解如下极值问题，更新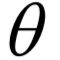的值：

 

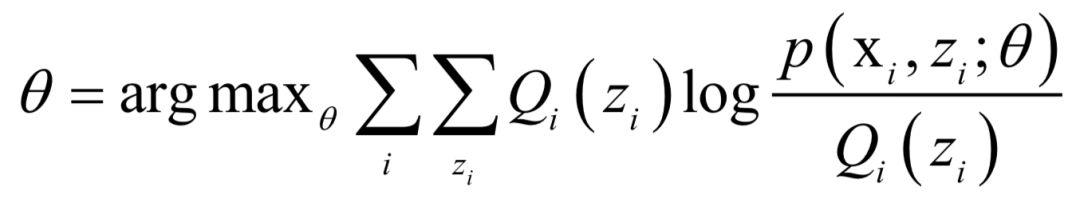
实现Qi 时可以按照下面的公式计算：

 

 

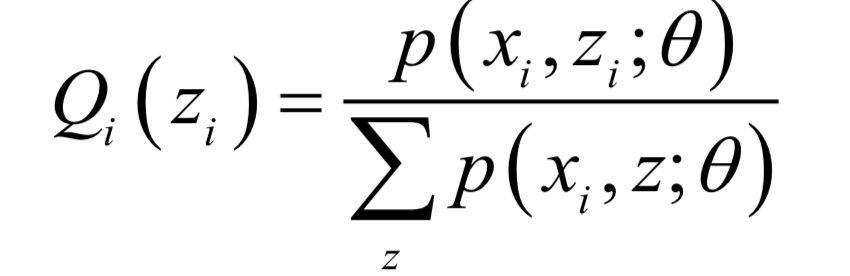
迭代终止的判定规则是相邻两次函数值之差小于指定阈值。需要注意的是，EM算法只能保证收敛到局部极小值。