test20230912

写在前面的话

考场估分 $100+100+20+30=250$ ，实际得分 $0+90+20+30=140$ 。这是停课以来挂分最为严重的一次，值得深思。挂分的原因也比较令人头疼，就是数组开大导致的 $\text{MLE}$ 。所以我决定以后的每一次考试都要测试使用的内存大小：

fprintf(stderr,"%.3lf MB",(&Med-&Mbe)/(1.0*1024*1024));

希望自己以后不要犯这种低级错误。

本场比赛在改完题之后觉得难度为 $\text{T3}-\text{T2}-\text{T1}-\text{T4}$ 。考试的时候偏执的认为啊 $\text{T1}$ 就是最简单的一道而和大多数人一样忽略了 $\text{T3}$ ，本来完全有实力打出这道题，但是不得不承认自己的考试策略有待进一步提升。

$T1$

题目描述

现在有一个长度为 $n$ 的排列 $a$ 。问交换两个元素最多可以让逆序对数量减少多少。

$n⩽{10}^6$ 。

思路点拨

题目非常的简洁，我提供一种自己的做法，不同于 $\text{std}$ 。

首先十分显然的，对于另个元素 $a_l,a_r$ ，如果 $l<r$ 并且 $a_l<a_r$ 我们就没有必要交换这两个元素，这只会给我们带来更多的逆序对数量，这里不考虑。

我们想一下，如果知道了我们需要交换 $l,r$ ，那么如何快速的计算贡献呢？假设我们将每一个元素按照柱状图的形式画出来：

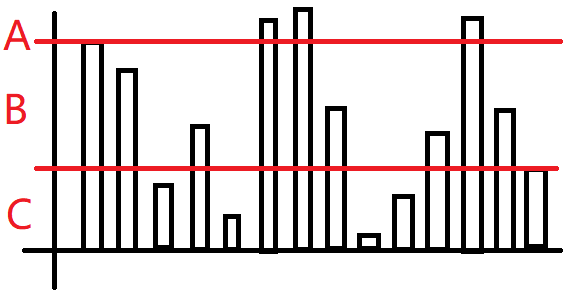
我们将这些数划分为三个部分：

• $A$ 部分：$a_i>a_l$ 。

• $B$ 部分：$a_r<a_i<a_l$ 。

• $C$ 部分：$a_i<a_r$ 。

首先，不在这个区间内的元素的逆序对关系并不会边，我们就只需要大胆的考虑这个区间内产生的变化。对于 $a_r$ 而言，与 $A+B$ 部分的元素产生了逆序对关系，而到了 $l$ 的位置之后则与 $C$ 部分的元素产生关系，贡献就是 $A+B-C$ 。对于 $a_l$ 而言，他与 $B+C$ 部分的元素产生了逆序对关系，但是到了 $r$ 的位置之后则与 $A$ 部分产生逆序对关系,贡献就是 $B+C-A$ 。

总体来说，贡献就是 $(A+B-C)+(B+C-A)=2B$ ，加上 $l,r$ 自身贡献了一个逆序对就是 $2B+1$。现在我们知道了，交换 $l,r$ 的贡献就是 $2\sum _{i=l}^r[a_r<a_i<a_l]$ 。如果需要统计的话，$O(n^2)$ 可以考虑二维前缀和。$O(n\log n)$ 可以考虑主席树，但是这都意义不大了，我们需要正解。

这样的结论显然是不足以写出正解，但是注意到交换 $l,r$ 的时候产生贡献的元素需要满足什么要求？$l<i<r$ ，并且 $a_r<a_i<a_l$ 。这是一个二维关系，我们考虑将 $(i,a_i)$ 看做一个点放进平面直角坐标系里面，然后问题就是我们需要选出一个矩形的左上角和一个右下角，要求矩形内的元素数量尽量多。

考虑什么样的左上角是有意义的。如果对于一个左上角 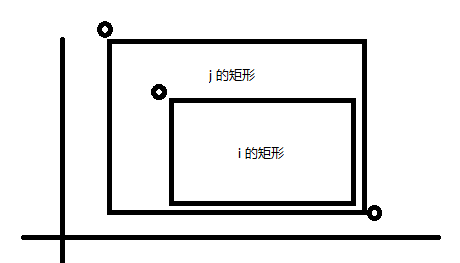$(i,a_i)$ ，存在 $(j,a_j)$ 满足 $j<i$ ，同事 $a_j>a_i$ ，那么 $i$ 就是没有意义的。因为如果我们选择 $j$ 作为左上角，以 $i$ 作为左上角的矩形在同一个右下角的情况下会被包含，所以只会让贡献变小，就比如说：

所以谁更加牛逼一目了然吧。我们继续考虑对于右下角有需要满足什么条件。如果存在节点 $(i,a_i)$ ，但是有 $(j,a_j)$ 有 $i<j$ ，同时 $a_i>a_j$ 。那么 $i$ 就是没有意义的。就比如说：

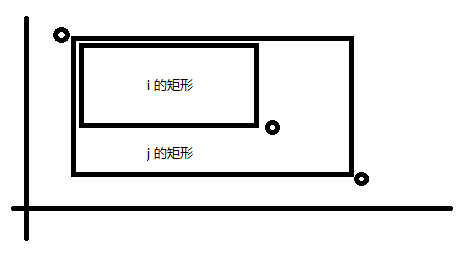
所以我们成功的缩小了左右端点的范围。接下来我们所说的左右端点只考虑这些有用的左右端点。

我们接下来考虑这些有用的左右端点会是什么样的呢？就拿左端点来举例子吧，如果有 $j<i$ ，那么如果 $i,j$ 都是合法端点，$a_j<a_i$ 是必须的。不然 $i$ 就会无效。对于右端点的约束也是十分的类似，$i<j$ 需要满足 $a_i<a_j$ ，否则 $i$ 无效。都是一个单调的关系啊，我们画一张图（想问题的时候鼓励多多画图帮助理解），其中圆圈是左上角端点，小方形是右下角端点：

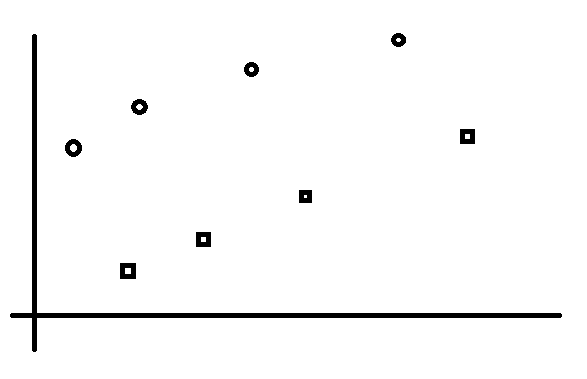
接下来，我们发现，一个元素对一些右下角端点做出贡献，并且这些右下角端点是一段连续的端点：

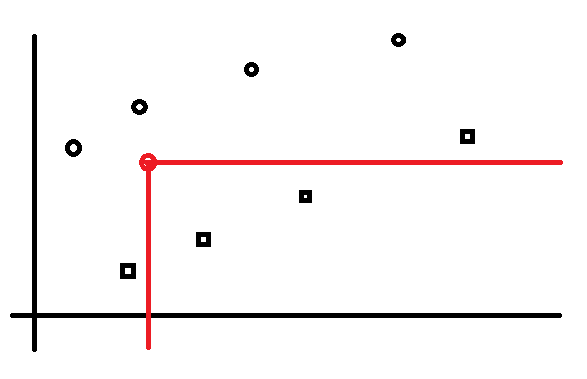
红色的部分就是可以产生贡献的左端点，显然是连续的。为什么会这样，这是因为右下角端点的单调性导致的，可以使用反证。可以感性理解一下，相信还是比较好懂的。同理，我们也就知道了，对于一个左上角来说，他可以使用的右下角是一段连续的区间。对于每一个节点（不论是否有效），我们都可以使用二分法求出那些左端点可以产生贡献，可以使用二分来求。

还是讲一下怎么来二分求吧。我们先对数组 $a$ 做后缀最小值 $m{n}_i=\underset{i⩽j}{min}\{a_j\}$ 。接下来，对于元素 $k$ 而言，我们希望找到一个尽量靠右的右下角节点满足 $a_k>a_i$ 。其实我们可以直接在二分的时候比较 $mn$ 的值。因为所有的右下角节点都一定出现在了后缀最小值里面。

	mn[n+1]=n+1;
	for(int i=n;i;i--) mn[i]=min(mn[i+1],a[i]);
	while(l<r){
		int mid=(l+r)/2+1;
		if(mn[mid]<i) l=mid;
		else r=mid-1;
	}

我们假设有一个数组 $s$ ，我们将全部的有效左端点按照从左到右的顺序存在了这个数组里面(存的下标)，一共有 $top$ 个元素。这里重要的事情再说一遍，$s_i<s_{i+1}$ ，单调性！！！ 这个待会会用到，别懵逼了。

我们先求出 $s_{top}$ 的贡献会是多少 。我们对于每一个 $i>s_{top}$ 将它的贡献以区间加的形式加到他可以产生贡献的那一段连续右端点上。那么 $s_{top}$ 就直接查他可以选择的左端点的贡献最大值就可以了(不用考虑多了， $a[s_{top}]=n$)，这还是一个连续的区间。现在我们就是需要维护的区间加法以及区间最大值查询，可以使用功能强大的线段树在单次 $O(\log n)$ 解决。

接下来，我们考虑 $s_{top}$ 向 $s_{top-1}$ 去转变求值对象，会产生什么问题。

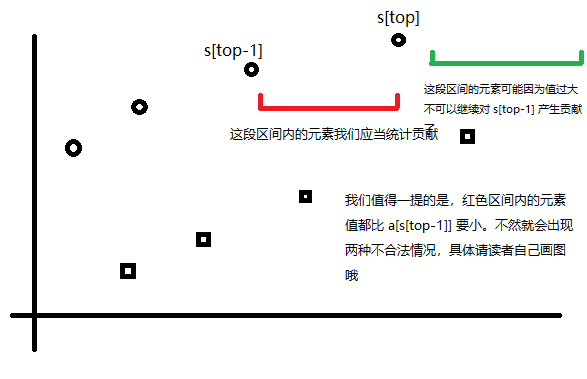
可以看见，我们就是剩下两个区间的内容需要统计，我们分开讨论：

• 红色部分

这一部分十分简单，我们直接暴力枚举每一个元素，然后再线段树上加入他的贡献就可以了。不会出现数值比 $s_{top-1}$ 大的情况，可以画画图。

• 绿色部分

我们可以维护一个大根堆，按照 $a_i$ 的大小排序的堆，表示目前产生贡献的元素集合。我们遍历到 $s_{top-1}$ 的时候我们可以从大根队中去除 $a[i]>a[s_{top-1}]$ 的元素的影响。

去除影响包含两个部分，一个是需要在线段树上删除对左端点的贡献；另一个是记得从堆中删除。由于每一个元素只会进入堆一次，出去一次，所以时间复杂度是有保障的。

最后，在加入红色部分的元素的时候也需要记得加入堆中。

现在我们知道了 $s_{top}$ 向 $s_{top-1}$ 的贡献转移，那么 $s_{top-1}$ 向 $s_{top-2}$ 的转移也是如法炮制。

总体时间复杂度 $O(n\log n)$ ，常数略大，需要卡卡常数才可以通过本题。

本题还是比较抽象，具体需要结合代码理解：

#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int MAXN=2e6+10;
int n,a[MAXN];
int mx[MAXN],mn[MAXN],tmp[MAXN];
int t[MAXN<<2],tag[MAXN<<2];
inline void pushup(int i){
	t[i]=max(t[i<<1],t[i<<1|1]);
}
inline void pushdown(int i){
	t[i<<1]+=tag[i],t[i<<1|1]+=tag[i];
	tag[i<<1]+=tag[i],tag[i<<1|1]+=tag[i];
	tag[i]=0;
}
inline int query(int i,int l,int r,int L,int R){
	if(L<=l&&r<=R) return t[i];
	if(l>R||r<L) return 0;
	int mid=(l+r)>>1;
	pushdown(i);
	int ans=max(query(i<<1,l,mid,L,R),query(i<<1|1,mid+1,r,L,R));
	pushup(i);
	return ans;
}
inline void update(int i,int l,int r,int L,int R,int w){
	if(L<=l&&r<=R){
		t[i]+=w,tag[i]+=w;
		return ;
	}
	if(l>R||r<L) return ;
	int mid=(l+r)>>1;
	pushdown(i);
	update(i<<1,l,mid,L,R,w);
	update(i<<1|1,mid+1,r,L,R,w);
	pushup(i);
}
int s[MAXN],top,suc[MAXN];
int temp[MAXN],cnt;
struct cmp{
	bool operator()(const int &a,const int &b){
		return a<b; 
	}
};
priority_queue<int,vector<int>,cmp> S; 
signed main(){
	freopen("2457.in","r",stdin);
	freopen("2457.out","w",stdout);
	n=read();
	for(int i=1;i<=n;i++) a[i]=read(),tmp[a[i]]=i;
	for(int i=1;i<=n;i++) mx[i]=max(mx[i-1],a[i]);
	mn[n+1]=n+1;
	for(int i=n;i;i--) mn[i]=min(mn[i+1],a[i]);
	for(int i=1;i<=n;i++){
		int l=tmp[i],r=n;
		while(l<r){
			int mid=(l+r)/2+1;
			if(mn[mid]<i) l=mid;
			else r=mid-1;
		}
		suc[i]=l;
	}
	for(int i=1;i<=n;i++)
		if(mx[i-1]<a[i]) s[++top]=i;
	for(int i=n;i>=s[top];i--){
		update(1,1,n,tmp[a[i]],suc[a[i]],1);
		S.push(a[i]);
	}
	int ans=0;
	for(int i=top;i;i--){
		int pos=s[i];
		while(!S.empty()){
			int it=S.top();
			if(it>=a[pos]){
				update(1,1,n,tmp[it],suc[it],-1);
				S.pop();
			}
			else break;
		}
		ans=max(ans,query(1,1,n,pos,suc[a[pos]])*2-1);
		for(int j=s[i];j>=s[i-1];j--){
			update(1,1,n,j,suc[a[j]],1);
			S.push(a[j]);
		}
	}
	cout<<ans;
	return 0;
}

这道题目让我大大的震撼，与 $T2$ , $T3$ 的难度形成了鲜明的对比，害得我死磕了很久。

不得不承认这的确是一道十分优秀的好题

$T2$

题目描述

现在有一个长度为 $n$ 的序列 $a$ 。每一次操作你可以选择一个 $i⩽n-2$ ，然后将 $(a_i,a_{i+1},a_{i+2})$ 变为 $(a_{i+1},a_{i+2},a_i)$ 。你需要在不超过 $n^2$ 次操作的前提下将其排序。

$n⩽{10}^3$ 。

思路点拨

我们发现，对于 $a_{i+1},a_{i+2}$ 个元素而言，每一次操作他们的位置向前移动一个，本质上和冒泡排序的交换差异不多，所以对于 $1$ 到 $n-2$ 个元素可以使用类似于冒泡排序的做法简单解决。

但是最后我们有两种情况：

$$1,2,3,3,3,3,5,6$$

没错，此时后面两个元素刚好是有序的，这样子我们就不需要处理了。

但是毒瘤的是最后两个元素不一定是有序的：

$$1,2,3,3,3,3,6,5$$

这样看起来没有什么头绪，但是是有解的，我们考虑一个更加简单的情况 $(3,3,5,4)$ 。

$$(3,3,5,4)\to (3,4,5,3)\to (5,4,3,3)\to (4,3,5,3)\to (4,5,3,3)\to (4,3,3,5)\to (3,3,4,5)$$

现在就可以处理出来了。这样操作的前提是存在两个相同切相邻的元素，如果 $1$ 到 $n-2$ 这些数互不相同的话，这种情况是一定不可以解决的，无解。但是不一定这两个相同的元素贴着 $a_{n-1},a_n$ ，就比如说：

$$3,3,4,5,6,7,9,8$$

我们可以移动 $(9,8)$ ，之后到达：

$$3,3,9,8,4,5,6,7$$

接下来按照类似于 $3,3,6,5$ 的方法处理，变成：

$$3,3,8,9,4,5,6,7$$

最后我们有将 $(8,9)$ 移动回去：

$$3,3,4,5,6,7,8,9$$

就完成了排序。

还是比较抽象，给出一份代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-') f=-f;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
const int MAXN=1e3+10,inf=1e10;
int n,a[MAXN];
int s[MAXN*MAXN],top;
void tran(int i,int j,int k){
    int x=a[i],y=a[j],z=a[k];
    a[i]=y,a[j]=z,a[k]=x;
}
void solve(int pos){
	int now=n-1;
	while(now-1>pos)
		s[++top]=--now;
	s[++top]=now-1,s[++top]=now-2;
	s[++top]=now-2,s[++top]=now-1;
	s[++top]=now-1,s[++top]=now-2;
	for(int i=now;i<n-1;i++)
		s[++top]=i,s[++top]=i;
}
signed main(){
    freopen("2458.in","r",stdin);
    freopen("2458.out","w",stdout);
    srand(time(0)); 
    n=read();
    for(int i=1;i<=n;i++)
        a[i]=read();
    for(int i=1;i<=n-2;i++){
        int mn=inf,pos;
        for(int j=i;j<=n;j++)
            if(a[j]<mn)
                mn=a[j],pos=j;
        while(pos>i){
            if(pos==i+1) tran(pos-1,pos,pos+1),s[++top]=pos-1;
            else tran(pos-2,pos-1,pos),s[++top]=pos-2;
            pos--;
        }
    }
    bool flag=0;
    for(int i=1;i<=3;i++){
        if(a[n-2]<=a[n-1]&&a[n-1]<=a[n]){
            flag=1;
            break;
        }
        s[++top]=n-2;
        tran(n-2,n-1,n);
    }
    if(!flag){
        for(int i=1;i<=n;i++)
        	if(a[i]==a[i+1]){
        		solve(i+1);
        		flag=1;
        		break;
			}
    }
    if(!flag) cout<<-1;
    else{
        cout<<top<<endl;
        for(int i=1;i<=top;i++)
            cout<<s[i]<<" ";
    }
    return 0;
}

$T3$

题目简述

给定一个长度为 $n$ 的二元组序列 $\{(a_i,b_i)\}$ 。

我们定义一个排列 $p$ 的价值为最小的 $i$ 满足：

$$\mathrm{\forall }j⩾i,\sum _{k=i}^j(a_{p_k}-b_{p_k})⩾0$$

$$\mathrm{\forall }j<i\sum _{i⩽k⩽n}(a_{p_k}-b_{p_k})+\sum _{1⩽k⩽j}(a_{p_k}-b_{p_k})⩾0$$

求全部排列的价值和。

$n⩽20$。

思路点拨

我们令 $w_i=a_i-b_i$ 。对于一个合法的局面以及一个最小的起点 $i$ ，应当满足如下约束:

• $\sum w_i⩾0$

• 对于 $\mathrm{\forall }j⩾i,\sum _{k=i}^j(a_{p_k}-b_{p_k})⩾0$

• 对于 $\mathrm{\forall }j<i,\sum _{k=j}^{i-1}(a_{p_k}-b_{p_k})<0$

对于第 $2$ 个约束条件是它应该的，但是作为最小的起点 $i$ ，需要满足第 $3$ 条约束条件。不然我们完全可以让这个起点 $i$ 往前移动变成更小的合法起点。

现在我们定义状态 $f_i,g_i,po{p}_i,su{m}_i$ 。$i$ 均指代一个二进制压缩数。$f_i$ 表示选择了集合 $i$ 的元素，排列出来的每一个后缀和都小于 $0$ 的方案数。$g_i$ 表示选择了集合 $i$ 的数，排列出来的每一个前缀都大于等于 $0$ 的方案数。$po{p}_i$ 表示集合 $i$ 的元素个数，$su{m}_i$ 表示集合 $i$ 的元素价值和。

答案就是 $\sum f_i{g}_{S-i}(po{p}_i+1)$ ，$S$ 表示全集。

转移的时候分两类讨论，对于一个集合，当 $su{m}_i<0$ 的时候，我们转移 $f$ 。当 $su{m}_i⩾0$ 时，我们转移 $g$ 。转移还是比较套路：

for(int i=1;i<(1<<n);i++){
	if(sum[i]<0){
		for(int j=0;j<n;j++)
			if(i&(1<<j))
				f[i]=(f[i]+f[i^(1<<j)])%mod;
	}
	else{
		for(int j=0;j<n;j++)
			if(i&(1<<j))
				g[i]=(g[i]+g[i^(1<<j)])%mod;
	}
}

时间复杂度 $O(n{2}^n)$ 。

$T4$

题目描述

现在给出 $n,m$ ，你需要求出所有满足相邻元素之和不等于 $m,m+1$ 的 $1$ 到 $n$ 的排列数量和。

对于 $100\mathrm{\%}$ 的数据，做法超纲。

对于 $80\mathrm{\%}$ 的数据，$n⩽{10}^9,m⩽{10}^3$ 。

思路点拨

如果我们元素 $i(i⩽m)$ 向 $m-i$ 和 $m-i+1$ 连边，表示不可以相邻，那么就会得到一个长度为 $m$ 的链和一些单点。我们的排列就是希望链上的节点不可以相邻。其中，对于长度为 $2$ 以及更长的链，可以正反放置所以方案乘 $2$ 。

我们定义状态 $f_{i,j}$ 表示有 $m$ 个元素组成的链，划分成了 $j$ 条子链，方案数是多少。答案考虑容斥：

$$ans=\sum _{i=0}^m(-1{)}^{m-i}\times f_{m,i}(n-m+i)!$$

为什么会是 $f_{m,i}(n-m+i)!$ 呢？就是我们把这写链和普通的元素一起做全排列问题。

$f$ 数组还是比较好求的，运用前缀和优化可以做到 $O(m^2)$ ，也就是状态数的级别，不可以继续优化。

至于阶乘，因为 $n⩽{10}^9$ 太大，我们只可以分块打表。