浅谈后缀数组
前置知识 : 后缀(???),基数排序(说通俗一点就是桶子排序)，基础倍增。
后缀数组是一种处理字符串问题的利器，可以起到代替后缀树的作用，在码量上具有绝对的优势。正常情况下，大家都会使用后缀数组而非后缀树。虽然后缀数组十分的好写，但是过程难以令人理解。今天我会使用尽量通俗的语言帮助大家理解什么是后缀数组，以及相关的拓展。
在开始之前
我们需要对于一些变量进行定义（别的数字在后边讲到）：
\(sa_i\) 表示排名为 \(i\) 的后缀下标是多少。
\(rk_i\) 表示下标 \(i\) 的后缀的排名是多少。
那么这两个数组是具有性质： \(sa[rk_i]=rk[sa_i]=i\) 。这一点看起来比较的绕，但是还是稍加思考可以理解的。也就是说，我们知道了 \(sa\) 和 \(rk\) 中的一者，就可以在线性的时间内推出另一个。
后缀排序
现在进行了定义，该如何求出这个后缀数组呢？我们讲如下两种方法（最最最最牛逼但是常数和码量极大的 \(\text{DC3}\) 我们暂不讨论）：
字符串哈希算法
这个算法的时间复杂度是 \(O(n \log^2 n)\) 。因为相比其他解法较劣势的时间复杂度，并不是很常使用。
相比大家知道怎么编写 \(std::sort\) 的自定义比较函数吧。如果这个比较的时间是 \(O(T)\) 的，那么我们的排序时间就可以做到 \(O(Tn \log n)\) 。那么现在我们的目标就是在尽量块的时间内比较两个后缀的字典序。
最简单的做法就是暴力的枚举，但是注意到 \(LCP\) (最长公共前缀) 是可以二分的，所以我们可以去二分第一个不一样的前缀，比较最后一个字符的大小就可以了。问题就又变换为了如何去比较两个字符串相同，这个显然使用字符串哈希可以在 \(O(1)\) 的时间内解决。那么我们的比较时间就从 \(O(n)\) 优化到了 \(O(n\log n)\) 。
最终的时间复杂度就是 \(O(n \log^2 n)\) 。
倍增算法
字符串哈希的算法并没有那么重要，就是一个优化的好的暴力，这个倍增的做法才是我们的重头戏，他的码量很小，并且实用性是最为广泛的。缺点还是有的，不是很好理解，所以请读者跟紧我的步伐一步步来。
第一步
我们先按照单个字符进行排序，这一部分可以使用单关键字基数排序。同时，我们可以预处理最初的 \(sa\) 数组。注意，这里 \(sa\) 数组所存储的值并不是我们一开始的定义。其中 \(sa_i\) 表示单个字符字典序排名为 \(i\) 的下标编号。
代码：
for(int i=1;i<=n;i++){
x[i]=s[i];
++temp[x[i]];
}
for(int i=1;i<=S;i++) temp[i]+=temp[i-1];
for(int i=n;i>=1;i--) sa[temp[x[i]]--]=i;
//这里x表示后缀i的排名，但是目前只考虑了每一个下标后第一个字符
//sa就是后缀数组，表示排名为i的后缀是多少
//temp就是一个用来排序的桶子。S表示字符集大小
第二步
我们考虑如果是要将以下标 \(i\) 为起点的 \(2\) 个字符排序要怎么办？比如：
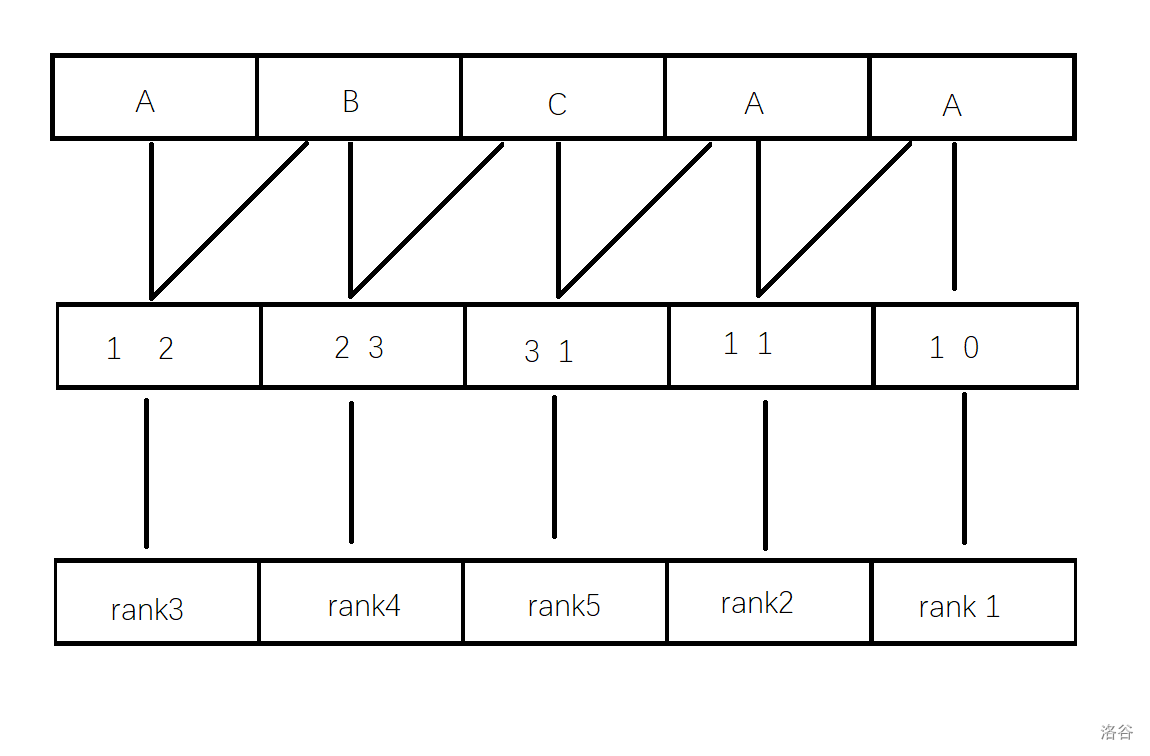
我们在第一步预处理的时候处理出了排名为 \(i\) 的后缀编号，那么我们可以以此推出 \(rk\) 数组。接下来，我们按照第一个字符为第一关键字，第二个字符为第二关键字排序就可以求出新的 \(sa\) 数组。就是上图所演示的。实际上，因为字符集比较小，所以使用基数排序优化到 \(O(n)\) 。
双关键字基数排序
单关键字的基数排序十分的简单，而双关键字基数排序的本质就是在单关键字排序的基础上，满足第二关键字有序。
我们可以先按照第二关键字进行第一遍基数排序，再按照第一关键字进行第二遍基数排序。为什么这个会是对的呢？因为基数排序是稳定的，我们在进行第一次基数排序之后，第二关键字有序，那么我们按照第一关键字排序之后，那些第一关键字相同的元素就会按照第二关键字顺序排好。可能比较抽象的解释吧。
那么我们知道了求解 \(2\) 个字符的情况，其实可以推广到求解 \(2^i\) 个字符的情况。
我们可以将一个长度为 \(2^i\) 的字串看成两半，一半是前 \(2^{i-1}\) 个字符，后一半就是另外 \(2^{i-1}\) 个字符。如果我们提前求出了长度为 \(2^{i-1}\) 时的 \(sa\) 数组，我们就可以按照上述求解的方法如法炮制，求出新的 \(sa\) 数组。
那么倍增的次数就是 \(\log n\) 次，总体时间复杂度为 \(O(n \log n)\) 。
这就是倍增法的主要思想，理解了思想，就到了最为毒瘤的代码了。
第三步
现在就是实现代码的时间了，我们按照一部分一部分解析代码以及一些常数优化。
假设目前我们倍增到了长度为 \(k\) 的字串，下述代码下标相同。保证 \(k\) 是 \(2\) 的正整数次幂。
首先是预处理，之前讲过了（第一步）：
for(int i=1;i<=n;i++){
x[i]=s[i];
++temp[x[i]];
}
for(int i=1;i<=S;i++) temp[i]+=temp[i-1];
for(int i=n;i>=1;i--) sa[temp[x[i]]--]=i;
//这里x表示后缀i的排名，但是目前只考虑了每一个下标后第一个字符
//sa就是后缀数组，表示排名为i的后缀是多少
后文，\(x\) 数组表示目前的 \(rk\) 数组。\(y\) 数组表示下标按照第二关键字排序后的数组。\(y_i\) 就表示第二关键字第 \(i\) 小的下标。
int pos=0;
for(int i=n-k+1;i<=n;i++) y[++pos]=i;
//循环到n-k+1的原因就是[n-k+1,n]这些后缀并没有第二关键字，所以排名因该考前
for(int i=1;i<=n;i++)
if(sa[i]>k) y[++pos]=sa[i]-k;
//这一部分在对第二关键字进行排序
//只有 sa[i]>k 才有第一关键字
为什么不需要进行基数排序呢？因为我们知道，第二关键字运用到的 \(sa\) 数组我们已经求出来了，所以顺序我们是提前知道的。
我们进行第二遍基数排序：
for(int i=1;i<=S;i++) temp[i]=0;
for(int i=1;i<=n;i++) temp[x[i]]++;
for(int i=1;i<=S;i++) temp[i]+=temp[i-1];
for(int i=n;i>=1;i--)
sa[temp[x[y[i]]]--]=y[i];
//这一部分函数调用比较复杂，但是可以联想到我们是怎么对s[1]-s[n]是如何基数排序的
//只不过是将i换成了排序完第二关键字的y数组罢了
之后，我们按照原来得 \(x\) 数组和 \(sa\) 数组推出新得 \(x\) 数组。
for(int i=1;i<=n;i++) y[i]=0;
swap(x,y);
//更新x数组需要运用到原来的x和原来的sa数组，所以暂时存储在y中
pos=1;
x[sa[1]]=1;
for(int i=2;i<=n;i++){
if(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])
x[sa[i]]=pos;
else x[sa[i]]=++pos;
}
代码还是比较好理解。后面的一部分本质上就是类似于离散化的一个过程。我们的第一，第二关键字都已经排好序了，处理排名就简单了。
我们还可以在最后加上两个优化：
if(pos==n) break;
//以上是一个小优化，就是如果目前所有的后缀都已经分出排名了，我们可以直接跳出
S=pos;
//因为此时x在1-pos这个值域，所以可以缩小值域优化基数排序
总体代码：倍增算法
至此，我们学会了后缀排序。
最长公共前缀（LCP）
谈到后缀数组的运用，一定离不开 \(\text{LCP}\) 和 \(\text{height}\) 数组。
我们定义 \(\text{LCP}(i,j)\) 表示后缀 \(sa_i,sa_j\) 的最长公共前缀，那么有如下结论：
进而推广：
对于第一个结论，给出如下证明：
我们假设 \(\min_{k=i}^j\{\min\{\text{LCP}(i,k),\text{LCP}(k,j)\}\}=p\) ，那么存在 \(p \leqslant \text{LCP}(i,j),p \leqslant \text{LCP}(i,k),\text{LCP}(k,j)\)
- 假设 \(\text{LCP}(i,j)>p\) ，可以有 \(\text{LCP}(i,j)=p+1\)
那么 \(s[sa_i+p+1]=s[s_j+p+1]\) ，可以 \(s[sa_i+p+1]\neq s[sa_k+p+1],s[sa_k+p+1]\neq s[sa_j+p+1]\) 。可以得到 \(s[sa_i+p+1]\neq s[sa_j+p+1]\) ，这与我们的假设相违背。
那么 \(\text{LCP}(i,j)<p\) 也是可以类似证明。根据这个结论，可以推广为结论 \(2\) ，还是比较显然。
我们定义 \(height(i)=\text{LCP}(i,i-1)\) , \(\text{LCP}(i,j)=\min_{k=i+1}^j\{height(k)\}\) 。可以发现 \(height\) 还是很重要的，但是我们没有什么好的办法快速求出来（虽然字符串hash可以 \(O(n \log n)\) 求，但是这并不够优美，并且可能会错）。我们又定义 \(h_i=height(rk_i)\) ，有一个逆天的结论：
有了这个结论，我们就可以在 \(O(n)\) 的时间求出 \(height\) 了。至于这个结论到底为什么是对的，，，，我也不知道。
给出求 \(height\) 的代码：
for(int i=1;i<=n;i++) rk[sa[i]]=i;
int pos=0;
for(int i=1;i<=n;i++){
if(rk[i]==1) continue;
pos=pos?pos-1:pos;
int j=sa[rk[i]-1];
while(i+pos<=n&&j+pos<=n&&s[i+pos]==s[j+pos]) pos++;
h[rk[i]]=pos;
}
推荐一些题目（我个人可能不是很讲的清楚，难度从低到高）：
纯纯板子：
后缀数组
[AHOI2013]差异
[HAOI2016] 找相同字符
并不全是板子：
[SDOI2016] 生成魔咒
[SDOI2008] Sandy 的卡片
[NOI2015] 品酒大会
