贪心，构造学习笔记

贪心构造不会

黄题绿题懵逼

横批：依托答辩

$CF1764C$

题目描述

有一些点，每一个点有一个点权 $a_{i}$ 。你可以在任意点之间连边，最终的图需要满足不存在 $a, b, c$ 满足 $a_{a} ⩽ a_{b} ⩽ a_{c}$ 并且 $a b, b c$ 之间有连边。

思路点拨

我们连出来的图一定可以被划分为一个二分图。不然就会存在奇环，而不论你怎么构造，奇环上就是会有一条路径不满足条件。

所以我们可以枚举一个值域的划分，假设枚举 $w$ 这个值，那么我们让 $a_{i} ⩽ w$ 的点进入左部，反之进入右部。我们最终可以让左部的每一个点都连向右部的每一个点，这样就可以满足条件。因为全部的二分图中，想要连边最多，全部的情况我们都考虑到了。

但是还存在一种极端的情况，就是划分不出来一个二分图使得左部和右部都非空，也就是说，全部的值都相等。这个时候，我们发扬人类智慧，让最终的图不存在长度为 $2$ 的路径就可以了，所以答案就是 $⌊ \frac{n}{2} ⌋$ 。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=2e5+10;
int T,n,a[MAXN];
signed main(){
	cin>>T;
	while(T--){
		cin>>n;
		for(int i=1;i<=n;i++) cin>>a[i];
		sort(a+1,a+n+1);
		int ans=0;
		for(int i=1;i<n;i++)
			if(a[i]!=a[i+1])
				ans=max(ans,i*(n-i));
		cout<<max(ans,n/2)<<endl; 
	} 
	return 0;
}

$Luogu3918$

题目描述

有一个飞行表演持续 $n$ 个单位时间，每一个单位时间都可以表演一种特技，共有 $k$ 种特技。表演具有价值之说，我们给定了一个长度为 $k$ 的序列 $c$ ，一次表演的价值就是距离上次表演这个特技的时间乘上 $c_{i}$ 。我们希望让表演的总价值最大。

思路点拨

我们考虑对于一种特技假设他出现位置的序列为 $p o s_{1}, p o s_{2}, . . ., p o s_{m}$ ，那么他的价值就是： $\sum_{i = 1}^{m - 1} (p o s_{i + 1} - p o s_{i}) c_{j}$ ，那么就是 $(p o s_{m} - p o s_{1}) c_{j}$ 。说人话就是这个特技最后出现的时间减去这个特技第一次出现的时间乘上 $c_{j}$ ，我们进而贪心的，每一个特技要么不出现，要么出现两次。

我们猜一个结论，我们按照 $c$ 从大到小排序，每一次找到最长的区间之后，让这个区间的左右端点都表演目前还未表演的， $c$ 最大的那个特技。比较抽象，代码就是：

for(int i=1;i<=k;i++) cin>>a[i];
sort(a+1,a+k+1,cmp);
int ans=0;
for(int l=1,r=n,pos=1;l<r;l++,r--)
	ans+=(r-l)*a[pos++];

但是为什么是对的呢？我们考虑使用交换法来证明。假设存在两个下表 $i, j$ ， $i, j$ 第一次出现的位置和最后一次出现的位置分别是： $l_{i}, l_{j}, r_{i}, r_{j}$ 。并且 $c_{i} > c_{j}$ ， $l_{i} < l_{j} < r_{j} < r_{i}$ 。那么如果存在：

(r_{j} - l_{i}) \times c_{j} + (r_{i} - l_{j}) \times c_{i} > (r_{i} - l_{i}) \times c_{i} + (r_{j} - l_{j}) \times c_{j}

(l_{i} - l_{j}) c_{i} > (l_{i} - l_{j}) c_{j}

因为 $(l_{i} - l_{j})$ 是负数，而 $c_{i} > c_{j}$ ，所以这种情况是不可能的，按照上述方法贪心有最优解。

$Luogu9209$

题目描述

有一个包含 $n$ 个停车位的停车场，里面的停车位排成了一排，最左边和最右边都是墙壁。

有 $n$ 辆车要按顺序依次停入这个停车场，在停入第 $i$ 辆车时，这辆车要停入的位置左右两边的空位越多，停进去需要的时间也就会越少，具体地，如果其左边连续的空位数量为 $l$ ，其右边连续的空位数量为 $r$ ，那么停入该辆车所需时间为 $W_{i} - L_{i} \cdot l - R_{i} \cdot r$ ，其中 $W_{i}, L_{i}, R_{i}$ 会给出（特别的，停车所需要的时间不会是负数，所以我们保证 $W_{i} \geq L_{i} \cdot n + R_{i} \cdot n$ ）。

对于连续空位的解释：例如，下图中箭头所指位置左边连续空位为 $1$ ，右边连续空位为 $2$ 。

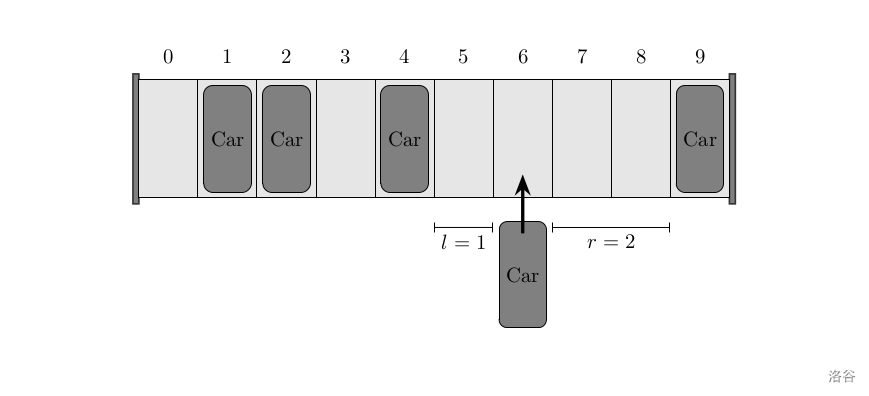
请依次确定每一辆车停入的位置，使得停入所有车所需时间最小。

思路点拨

结论：每一次对于一辆车，如果 $L > R$ 就停在最右边；如果 $L < R$ 就停在最左边。

正确性的话，每一次，我们可以让当前的车贡献最大，并且还可以让目前的车位连续，为后面的车达到最大贡献提供条件。

所以这是一个巧妙的安排方式，一举两得。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=2e5+10;
int n,w[MAXN],l[MAXN],r[MAXN];
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>w[i];
	for(int i=1;i<=n;i++) cin>>l[i];
	for(int i=1;i<=n;i++) cin>>r[i];
	int ans=0;
	for(int i=1;i<=n;i++)
		ans+=w[i]-(n-i)*max(l[i],r[i]);
	cout<<ans;
	return 0;
}

$Luogu6155$

题目描述

给定一个长度为 $n$ 的整数序列 $a_{i}$ ，再给定一个长度为 $n$ 的整数序列 $b_{i}$ 。

你可以进行一些修改，每次你可以将一个 $a_{i}$ 增加 $1$ ，花费为 $b_{i}$ ，你需要使所有的 $a_{i}$ 不相等，且同时满足花费最少。

但 zbw 认为太过简单，于是他规定，你可以在修改前进行无限次如下操作：交换 $b_{i}, b_{j} (1 \leq i, j \leq n)$ 。

求最小的花费。

思路点拨

我们考虑如果 $b_{i}$ 一样，该怎么操作。一个十分显然的结论就是，最后形成的那个序列是一定的。

我们考虑如何构造那个序列，我们维护一个集合，每一次我们加入一个数 $a_{i}$ ，如果 $a_{i}$ 没有出现在集合中，我们直接加入集合，反之我们可以找到第一个大于 $a_{i}$ 的还未出现的数，要求 $O (\log n)$ 维护。我们发现，我们维护的集合在数轴上，是一段一段分布的。每一次我们加入一个数，无非也就三种决策：

加入到一条链的底部
加入到一条链的顶部
加入到一条新链

这三种操作我们可以使用并查集维护，因为数组开不下（ $1 e 9$ 值域），所以使用 $M a p$ 优化。

最后我们就获得了这个序列。

考虑答案的计算，有两种方式：

第一种

我们将原来的序列 $a$ 和新的序列 $c$
分别从小到大排序，每一次计算答案就是 $\sum_{i = 1}^{n} c_{i} - a_{i}$ 。

第二种

我们在在线维护这个并查集的时候，我们的一个元素 $a_{i}$ 加入到集合中就会返回一个新的值 $c_{i}$ 表示因该加到 $c_{i}$ 上去，我们去 $d_{i} = c_{i} - a_{i}$ ，那么 $\sum d_{i} = \sum c_{i} - a_{i}$ ,所以贡献还是一定的。

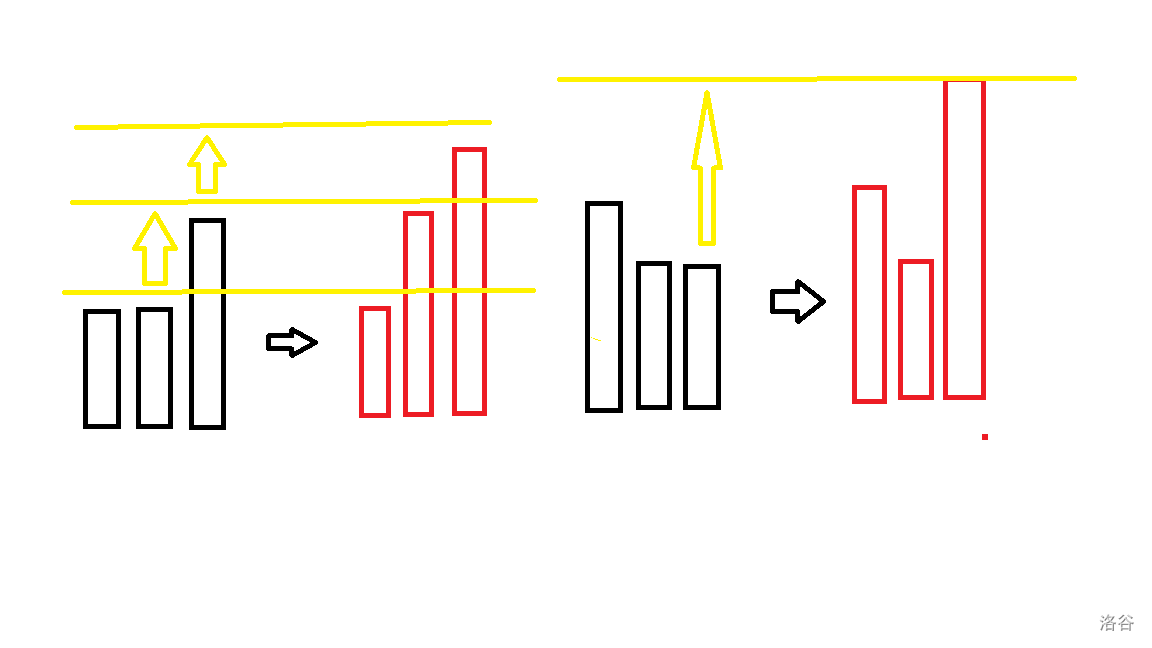
接下来考虑加入权值 $b$ 该怎么做，我们可以先将 $b$ 排个序。接下来的操作就是，我们需要在满足 $\sum d_{i}$ 不变的情况下，还要让改动的数尽可能小。一种解决方案就是，我们将 $a$ 数组按照从大到小的顺序加入并查集，这样我们每一次求出的 $d_{i}$ 就是更为连续的。这里放出张图：

这样子我们的答案不会变（都是 $\sum c_{i} - a_{i}$ ）但是我们可以让 $d_{i}$ 的分布更为集中。为什么需要让 $d_{i}$ 集中的原因就是可以让一个比较小 $b_{i}$ 产生更多的价值。并且，这是让 $d_{i}$ 最为集中的方法，它让需要改变的 $a_{i}$ 的数量做到了最少。

最终，我们将如上述方法得出的 $d_{i}$ 按照从大到小排序， $b$ 按照从小到大排序，答案就是：

$\sum d_{i} b_{i}$ 。

时间复杂度 $O (n \log n)$ 。

代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e6+10;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	} 
	return x*f;
}
void print(__int128 x){
	if(x<10) putchar(x+'0');
	else{
		print(x/10);
		putchar(x%10+'0');
	}
}
int n,a[MAXN],b[MAXN];
int fa[MAXN],temp[MAXN];
int find(int x){
	if(fa[x]==x) return x;
	return fa[x]=find(fa[x]);
}
map<int,int> vis;
bool cmp(int x,int y){
	return x>y;
} 
signed main(){
	n=read();
	for(int i=1;i<=n;i++) a[i]=read();
	for(int i=1;i<=n;i++) b[i]=read();
	sort(a+1,a+n+1,cmp);
	for(int i=1;i<=n;i++){
		int w=a[i];
		if(!vis[a[i]]){
			vis[a[i]]=i;
			fa[i]=i;
		}
		else{
			int dad=find(vis[a[i]]);
			a[i]=a[dad]+1;
			vis[a[i]]=i;
			fa[dad]=fa[i]=i;
		}
		if(vis[a[i]+1]) fa[i]=vis[a[i]+1];
		temp[i]=a[i]-w;
	}
	sort(b+1,b+n+1);
	sort(temp+1,temp+n+1,cmp);
	__int128 ans=0;
	for(int i=1;i<=n;i++)
		ans=ans+temp[i]*b[i];
	__int128 mod=1;
	for(int i=1;i<=64;i++) mod=mod*2;
	print(ans%mod);
	return 0;
}

$Luogu 9207$

题目描述

有一台计算器，使用 $k$ 位的带符号整型来对数字进行存储。也就是说，一个变量能够表示的范围是 $[- 2^{k - 1}, 2^{k - 1})$ 。现在我们希望使用该计算器计算一系列数 $a_{1}, a_{2}, \dots, a_{n}$ 的和。计算的伪代码如下：

由于奇怪的特性，如果两个变量在相加时得到的结果在 $[- 2^{k - 1}, 2^{k - 1})$ 之外，即发生了溢出，那么这台计算器就会卡死，再也无法进行计算了。

为了防止这样的事情发生，一个变通的方法是更改 $a_{i}$ 的排列顺序。容易发现这样不会改变计算出的和的值。

不过，可能不存在一种方案，使得计算出这 $n$ 个数并且计算机不爆炸。但我们还是希望，计算出尽量多的数字的和。

对于全部数据，保证 $1 \leq n \leq 500$ ， $1 < k \leq 8$ ， $- 2^{k - 1} \leq a_{i} < 2^{k - 1}$ 。

思路点拨

我们发现，数据保证 $- 2^{k - 1} \leq a_{i} < 2^{k - 1}$ ,也就是说，对于一些 $- 2^{k - 1} ⩽ s u m < 2^{k - 1}$ 的数，一定存在一种构造方案满足不会爆出计算范围，具体证明如下：

当我们的和大于 $0$ 的时候，我们就加最大的负数，一定不会小于 $- 2^{k - 1}$ 。当我们的和小于 $0$ 的时候，我们就加最小的正数，因为正数， $2^{k - 1}$ ,所以不会超出上限。

我们希望找到最多的数满足他们的和在 $[- 2^{k - 1}, 2^{k - 1})$ 之间。

我们可以按照我们之前的构造方案，我们会选正数从小到大排序的前缀和，我们会选负数从大到小排序的后缀和，因为数据比较小，我们可以直接枚举。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e3+10;
int N,k;
int n,a[MAXN],m,b[MAXN];
bool cmp(int x,int y){
	return x>y;
}
signed main(){
	cin>>N>>k;
	for(int i=1,w;i<=N;i++){
		cin>>w;
		if(w<0) b[++m]=w;
		else a[++n]=w; 
	}
	sort(a+1,a+n+1);
	sort(b+1,b+m+1,cmp);
	for(int i=1;i<=n;i++) a[i]+=a[i-1];
	for(int i=1;i<=m;i++) b[i]+=b[i-1];
	int ans=0;
	for(int i=0;i<=n;i++)
		for(int j=0;j<=m;j++)
			if(a[i]+b[j]<pow(2,k-1)&&a[i]+b[j]>=-pow(2,k-1))
				ans=max(ans,i+j);
	cout<<ans;
	return 0;
}

$CF1707A$

题目描述

哆来咪·苏伊特参加了 $n$ 场比赛。比赛 $i$ 只能在第 $i$ 天进行。比赛 $i$ 的难度为 $a_{i}$ 。最初，哆来咪的 IQ 为 $q$ 。在第 $i$ 天，哆来咪将选择是否参加比赛 i。只有当她当前的 IQ 大于 $0$ 时，她才能参加比赛。

如果哆来咪选择在第 $i$ 天参加比赛 $i$ ，则会发生以下情况：

如果 $a_{i} > q$ ，哆来咪会觉得自己不够聪明，所以 $q$ 将会减 $1$ ；
否则，什么都不会改变。

如果她选择不参加比赛，一切都不会改变。哆来咪想参加尽可能多的比赛。请给哆来咪一个解决方案。

思路点拨

我们考虑操作的逆操作，就是我初始的 $q = 0$ 。每一次我倒叙查看这些比赛，如果 $a_{i} > q$ ，我们就让 $q + 1$ 。但是 $q$ 有一个上限。问构造方案。

显然，我们倒叙的话肯定是能选就选呗。当我们的 $q$ 到达上限的时候我们记录一个下标 $p o s$ 。也就是说， $p o s$ 之后的比赛都是可以参加的。但是 $p o s$ 之前的比赛只有在不影响 $i q$ 的前提下才可以参加，即 $a_{i} ⩽ q$ 。

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	} 
	return x*f;
} 
const int MAXN=1e5+10;
int T,n,q,a[MAXN]; 
bool vis[MAXN];
signed main(){
	T=read();
	while(T--){
		n=read(),q=read();
		for(int i=1;i<=n;i++) a[i]=read();
		int cnt=0,pos=0;
		memset(vis,0,sizeof(vis));
		for(int i=n;i;i--){
			if(a[i]>cnt) cnt++;
			if(cnt==q){
				pos=i;
				break;
			}
		}
		for(int i=1;i<pos;i++)
			if(a[i]<=q) vis[i]=1;
		for(int i=pos;i<=n;i++)
			vis[i]=1;
		for(int i=1;i<=n;i++) cout<<vis[i];
		cout<<endl;
	}
	return 0;
}

$CF1779C$

题目描述

定义长度为 $n$ 的数组 $a r r$ 的前缀和数组为 $s$ ，对于一次操作，你可以选择一个数，变为这个数的相反数，给定一个数 $m$ ，请你求出最小的操作次数使序列满足： $\forall i \in [1, n], s_{i} \geq s_{m}$ 。

思路点拨

我们可以简化问题，由于对于 $m < i ⩽ n$ 的下标 $i$ ，都有 $s u m_{i} = (s u m_{i} - s u m_{m}) + s u m_{m}$ 。所以说我们可以不用考虑之前的那些数。原问题就可以拆分为两个更加特殊的子问题：

对于 $1 ⩽ i < m$ ，都有 $s u m_{m} ⩽ s u m_{i}$
对于 $m < i ⩽ n$ , 都有 $s u m_{m} ⩽ s u m_{i}$ 。

为什么拆分成两个子问题还是可以满足操作次数最小呢？因为对于 $1 ⩽ i < m$ 的那些操作，都会印象 $a_{m}$ 以及 $m < j ⩽ n$ 的 $a_{j}$ ，就等价于没有操作。所以两个子问题不会互相影响。

那么我们就分别讲解两个子问题的解法。但是因为两个子问题是镜像的，学会一个就会另一个，这里拿子问题 $1$ 作为讲解。

我们考虑什么时候 $s u m_{i} < s u m_{m} (i < m)$ ，也就是说：

\sum_{j = 1}^{i} a_{j} < s u m_{j = 1}^{m} a_{j}

0 < \sum_{j = i + 1}^{m} a_{j}

也就是说，对于每一个 $\sum_{i = p o s}^{m} a_{i}$ 都非负。我们维护一个指针从 $m$ 扫到 $1$ ，当我们发现了 $\sum_{i = p o s}^{m} a_{i} < 0$ 的时候，我们就需要在 $p o s$ 到 $m$ 中选择一个数取反，显然，我们希望这个数的相反数尽量的大。我们可以使用一个堆来进行维护。时间复杂度 $O (n \log n)$ 。

#include<bits/stdc++.h>
#define int long long
using namespace std;

inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar(); 
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int MAXN=1e6+10;
int T,n,m,a[MAXN];
struct cmp1{
	bool operator()(int a,int b){
		return a<b;
	}
};
struct cmp2{
	bool operator()(int a,int b){
		return a>b; 
	}
};
priority_queue<int,vector<int>,cmp1> q1;
priority_queue<int,vector<int>,cmp2> q2;
signed main(){
	T=read();
	while(T--){
		n=read(),m=read();
		for(int i=1;i<=n;i++)
			a[i]=read();
		if(n==1){
			cout<<0<<endl;
			continue;
		}
		int ans=0;
		while(!q1.empty()) q1.pop();
		while(!q2.empty()) q2.pop();
		int cnt=0;
		for(int i=m;i>1;i--){
			cnt+=a[i];
			q1.push(a[i]);
			if(cnt>0){
				cnt-=q1.top()*2;
				q1.pop();
				ans++;
			}
		}
		cnt=0;
		for(int i=m+1;i<=n;i++){
			cnt+=a[i];
			q2.push(a[i]);
			if(cnt<0){
				cnt-=q2.top()*2;
				q2.pop();
				ans++;
			}
		}
		cout<<ans<<endl;
 	} 
	return 0;
}

$Luogu5369$

题目描述

小 C 是一个算法竞赛爱好者，有一天小 C 遇到了一个非常难的问题：求一个序列的最大子段和。

但是小 C 并不会做这个题，于是小 C 决定把序列随机打乱，然后取序列的最大前缀和作为答案。

小 C 是一个非常有自知之明的人，他知道自己的算法完全不对，所以并不关心正确率，他只关心求出的解的期望值，现在请你帮他解决这个问题，由于答案可能非常复杂，所以你只需要输出答案乘上 $n!$ 后对 $998244353$ 取模的值，显然这是个整数。

注：最大前缀和的定义： $\forall i \in [1, n]$ ， $\sum_{j = 1}^{i} a_{j}$ 的最大值。

对于 $100 %$ 的数据，满足 $1 \leq n \leq 20$ ， $\sum_{i = 1}^{n} | a [i] | \leq 10^{9}$ 。

思路点拨

我也不知道为什么 $d p$ 被扔到了贪心构造里边。但是这个数据范围因该是 $d p$ 了。

我们考虑状态压缩动态规划，一般的状态不好转移，因为转移需要利用到最大值。但是，我们发现这样的最大值只有 $2^{n}$ 种。我们考虑枚举一个集合 $s$ ，让 $s$ 中每一个元素的和作为序列的最大前缀和，那么他产生的价值就是 $s u m_{s} \times f_{s} \times g_{(} A L L - s)$ 。其中：

$s u m_{s}$ 表示 $S$ 中的元素的价值之和。
$f_{s}$ 表示集合 $S$ 构成的序列中，有多少个序列满足最大前缀和等于 $s u m_{s}$ 。
$g_{s}$ 表示集合 $S$ 构成的序列中，有多少个序列满足最大前缀和是负数。
$A L L$ 表示全集。

转移的话， $g$ 的转移时比较套路:如果目前的集合 $S$ 的 $s u m_{S} < 0$ 那么就有：

g_{S} = \sum_{i \in S} g_{S - i}

$f$ 的转移就没有那么简单了，我们可以将一个没有在集合 $S$ 内的数放入序列的首部，这样每一个先前的前缀都会加上这个数的值，这样可以通过刷表转移：

f_{S + i} = f_{S} (0 ⩽ s u m_{S}^i \notin S)

最终统计答案即可。本题的难点在于将一个数放进序列的首部转移并没有那般好像，并且 $f$ 数组的边界需要仔细考虑，具体见代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;

inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar(); 
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int MAXN=20,mod=998244353;
int n,a[MAXN];
int sum[1<<20],f[1<<20],g[1<<20]={1};
signed main(){
	n=read();
	for(int i=0;i<n;i++) a[i]=read();
	for(int i=1;i<(1<<n);i++)
		for(int j=0;j<n;j++)
			if(i&(1ll<<j)) sum[i]+=a[j];
	for(int i=0;i<n;i++) f[1<<i]=1;
	for(int i=1;i<(1<<n);i++){
		if(sum[i]>=0){
			for(int j=0;j<n;j++)
				if(!(i&(1ll<<j)))
					f[i|(1ll<<j)]=(f[i]+f[i|(1ll<<j)])%mod;
		}
		else{
			for(int j=0;j<n;j++)
				if(i&(1ll<<j)) g[i]=(g[i]+g[i^(1ll<<j)])%mod;
		}
	}
	int ans=0,all=(1<<n)-1;
	for(int i=1;i<(1<<n);i++)
		ans=(ans+f[i]*g[all^i]%mod*(sum[i]+mod))%mod;
	cout<<ans;
	return 0;
}

posted @ 2023-08-20 11:48 Diavolo-Kuang 阅读(30) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 随题记录20230915

· 成都集训-test0717

· 贪心构造题目

· 贪心构造专题

· codeforces 构造题专题（easy version）

阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· ollama系列1：轻松3步本地部署deepseek，普通电脑可用
· 按钮权限的设计及实现
· 25岁的心里话

公告

昵称： Diavolo-Kuang
园龄： 1年9个月
粉丝： 0
关注： 0

+加关注

2025年3月

日

一

二

三

四

五

六

Diavolo

贪心，构造学习笔记

贪心构造不会

黄题绿题懵逼

横批：依托答辩

$CF1764C$

题目描述

思路点拨

$Luogu3918$

题目描述

思路点拨

$Luogu9209$

题目描述

思路点拨

$Luogu6155$

题目描述

思路点拨

第一种

第二种

$Luogu 9207$

题目描述

思路点拨

$CF1707A$

题目描述

思路点拨

$CF1779C$

题目描述

思路点拨

$Luogu5369$

题目描述

思路点拨

公告

搜索

常用链接

随笔分类

随笔档案

相册

阅读排行榜

评论排行榜

最新评论