成都集训游记

~~换个地方被吊打~~

Day1

今天主要是考试和讲题，但是今天我生病了头痛欲裂，所以没有写什么题，主要是休息吧。晚上吃了一些药，情况稍有改善后改了两道题。

数据结构专题（金天）

Day2

今天上午是自己写题，下午讲解了数据结构。学习的新知识是：

ZKW线段树
圆方树和点双tarjan

对于一些数据结构的trick有了新的理解。

A - Ice-cream Tycoon

题意：要求维护一个冰激凌集合，支持如下两种操作：

加入 $n$ 个价值为 $c$ 的冰激凌
出售最便宜的 $n$ 个冰激凌。如果这些钱大于 $v$ ，不操作，并且报告 $U n h a p p y$ ；反之删去这些冰激凌，返回 $H a p p y$ 。

思路点拨：本题比较简单

考虑对于全部的询问离线下来后离散化，使用线段树上二分判断是否买得起。十分基础，时间复杂度 $O (n \log n)$ 。

B - New Year Tree

给定一棵树，每一个节点有一个颜色。你需要编写一种数据结构，支持如下两种操作：

将子树全部的颜色改为 $c$ 。
询问字数内的颜色有多少种。

数据保证所有颜色的数量不超过 $60$ 种。

思路点拨：本题比较简单

考虑通过 dfs序将树上问题转化为序列上问题。
我们使用一个线段树维护区间上的颜色。对于一个区间的颜色表示，我们使用一个二进制压缩的数表示即可。pushup函数就两个儿子的颜色并。
子树颜色赋值就是区间赋值操作，维护一个懒标记。

时间复杂度 $O (n \log n)$ 。

C - Ping-Pong

你需要维护一个区间集合，支持如下两种操作：

添加一个区间[l,r] ，保证这个区间的长度严格大于之前的全部区间
查询第 $i$ 个区间是否可以直接或间接到达第 $j$ 个区间。我们认为两个区间 $[l 1, r 1]$ 和 $[l 2, r 2]$ 可以到达,就是 $l 2 < l 1 < r 2$ 或者 $l 2 < r 1 < r 2$ 。注意，这种到达是一种单向到达的关系。

思路点拨：本题十分困难

我们考虑对于第 $i$ 个区间，我们要到达区间 $j$ ，我们可以不断地往右走或者往左走，找到这个极大区间 $[l, r]$ 。我们对于区间 $j$ ，按照同样的方法找到极大区间 $[x, y]$ 。如果这两个区间满足 $[l, r]$ 到 [x,y] 有单向到达关系或者 $[l, r]$ 和 $[x, y]$ 本质是一样的，可以证明区间 $i$ 和区间 $j$ 可达。这个证明比较繁琐，但是画画图是可以推出来的。没有这个结论做不了这题，这也是本题的难点。
我们考虑维护一种数据结构，通过并查集的方式让每一个区间指向它可以到达的极大区间。我们维护这些极大区间。那么每一次加入一个区间的时候，我们可以将跟这个区间有交的极大区间给合并起来，形成一个新的极大区间。问题是，我们怎么找到有交的区间呢？
我们考虑对于每一个线段树的节点维护一个set，那么每一次添加一个区间，我们就将在线段树上被这个区间完全包含的 $\log n$ 个区间（这是指线段树上的区间，下同）的集合种添加一个标记。每一次合并的时候，我们又找到与这个区间有交集的 $\log n$ 个区间，将标记区间所在的极大区间合并起来。最后删去这个无用标记。
我们考虑计算时间复杂度，每一次我们打上 $O (\log n)$ 个标记。这些标记会被标记一次，又被删除一次，所以时间复杂度是 $O (n \log n)$ 的。

D - Life as a Monster

题意：平面上有 $n$ 个点，你需要编写一个程序支持如下两种操作：

更改一个点的坐标
查询某一个点到其余点的切比雪夫距离之和

强制在线，空间比较紧张。

思路点拨：本题难度适中

切比雪夫距离转曼哈顿距离。
我们考虑一个点距离其余点的曼哈顿距离可以转化为 $\sum | x - x_{i} | + | y - y_{i} |$ 。我们发现横纵坐标是相对独立的，所以我们分别考虑。剩下的部分使用一个动态开点权值线段树维护坐标和即可。

主要是切比雪夫距离转曼哈顿距离的trick需要知道。

E - Tourists

题意：给定了一个无向图，点有点权。你需要编写一个程序支持如下两种操作：

更改一个点的点权
查询在 $u, v$ 的路径上，在不经过相同点的情况下可以到达的最小点权。

思路点拨：本题难度适中

考虑一个联通块什么时候可以在不经过重复点的情况下到达任意点，这是一个点双。
我们考虑建立一个圆方树，方点维护这个点双的最小点权。但是每一次更改可能牵扯到多个方点，所以我们钦定一个根，并且让一个方点只管辖它的儿子节点的最小权值，这样的时间是正确的。
每一次查询，我们在圆方树上树剖求链上最小值，如果LCA是一个方点，答案就考虑这个方点的父亲节点的点权。

F - New Year and Conference

题意：现在有两个会场，每一个演出会在 $[l 1, r 1]$ 在会场1演出， $[l 2, r 2]$ 在会场二演出。问是否存在一个子集 $S$ ，是的这个自己中的演出在第一个会场没有交集，在第二个会场中存在时间重合。

思路点拨：本题比较简单。

其实 S 的大小我们只要考虑 $| S | = 2$ 。这个结论是很容易知道的。
我们考虑枚举重叠的区间的时间靠后的一个区间，双指针扫出哪些与这个区间的另一会场没有时间交集的那些区间，接下来考虑在这些区间中是否存在区间与本区间有交集。这样我们维护一个线段树判断是否有交集就可以了。

Day3

A Roadside Trees(*3000)

题目描述

路边有 $n$ 个位置，每一个位置可能生长着一棵树。每棵树每个月生长了一个高度，每一个月的开始，会进行如下操作之一：
在 $p$ 位置种植一颗高度为 $h$ 的树。
砍掉从左往右第 $c$ 颗树，这个位置不能再种树。
$h, c ⩽ 10$ 。

保证任意时刻不存在两颗高度相同的树。

每一次操作后查询最长上升子序列。

思路点拨

我们发现树会长高，十分烦躁。当我们种下一棵树的时候，我们将树的初始高度减去目前的时间 $T$ 。这样就转换成了静态问题，不需要考虑树生长的结果。

我们考虑到一半的最长上升子序列的转移柿子，对于一个元素 $c$ ，我们如果需要去除这个元素，只会对下标小于 $c$ 的元素造成影响，所以我们可以轻松解决第二个操作。

又因为树的高度两两不同，所以对于插入的一颗高度小于等于 $10$ 的树，至多对 $10$ 颗树造成影响。

时间复杂度 $O (10 n \log^{2} n)$ ，可以通过。

B Noble Knight's Path（*3000）

给一棵树，现在有两种询问：
标记某个节点
找到路径 $a - > b$ 再第 $k$ 次询问到当前询问之间没有被标记的第 $k$ 个节点。

思路点拨

对于在 $k$ 次操作之后的关于标记的维护，考虑主席树，这样十分方便。加上树上询问，套树剖。

特别的，在路径的 $L C A$ 处需要特别处理。
时间复杂度 $O (n \log^{2} n)$ 。

C 区间本质不同子串个数

$SAM$ 的题，太逆天。

D Cyclic Distance

太逆天，待补。

E HUD 7144 Treasure

给定一张边带权的无向图，每个点有一个颜色和一个权值。保证对于一种颜色，拥有这个颜色的点数不超过 10。现在要求支持以下两种操作
增加一个点的权值。
询问从一个点出发，不经过边权超过 x 的边，其所有可能到达的点中，每个颜色的最大权值之和。

思路点拨

对于边权限定这一块，考虑使用 $Kruskal$ 重构树转换成子树问题。

那么对于一个节点，我们需要增加权值的话，我们只需要找到从它开始，可以在哪一段路径上成为最大值。这个可以路径修改操作，使用树剖。查询自然不在话下。

时间复杂度 $O (10 n \log^{2} n)$ 。

考虑到颜色的数量十分的稀少，所以完全可以建虚树，时间复杂度 $O (10 n \log n)$ 。

G-JOI 稻草人/手办

题目描述

二维平面上有 $n$ 个节点，问有多少点对 $i, j$ 满足：

$x_{i} < x_{j}, y_{i} < y_{j}$
不存在 $x_{i} < x_{k} < x_{j}, y_{i} < y_{k} < y_{j}$ 。
$n ⩽ 2 \times 10^{5}$ 。

思路点拨

离散化后即为给定一个排列，要求找出 $i < j$ 满足 $p_{i} < p_{j}$ ，不存在 $i < k < j$ 满足 $p_{i} < p_{k} < p_{j}$ 。
复杂二元组计数考虑进行分治，固定左侧 $i$ 考察右侧有多少 $j$ 满足要求。
$i$ 在左部的后缀中最小的大于 $p_{i}$ 的元素给出 $j$ 最大值的限制，另外 $j$ 在右部的前缀中不能有 $p_{i} < p_{k} < p_{j}$ 的 $p_{k}$ 。
不妨按照大小顺序，从大到小加入 $p_{i}$ 。同时维护所有满足条件 $> p_{i}$ 的 $p_{j}$ 。加入一个 $j$ 时， $p_{j}$ 右侧的所有 $j^{'}$ 显然满足 $p_{i} < p_{j} < p_{j}^{'}$ ，需要删除。这样可能的 $j$ 形成 $p_{j}$ 单调下降的序列，可以二分求出最后一个满足条件的 $j$ 。
通过单调栈维护可能的 $j$ ， $BIT$ 记录前缀和
复杂度 $O (n \log n \log n)$ 。

String 专题（冯施源）

[NOI2014]动物园

题目描述

我们给定一个字符串 $S$ ，定义 $n u m [i]$ 表示 $S$ 的前 $i$ 个字符组成的字符串中，长度小于等于 $⌊ \frac{i}{2} ⌋$ 的 $b o r d e r$ 数量。求 $\sum (n u m [i] + 1)$ 。

$| S | ⩽ 1 e 6$

思路点拨

我们考虑一个暴力，我们可以使用 $KMP$ 算法先求出 $f a i l$ 数组和一个 $d p$ 数组。其中 $d p_{i}$ 表示字符串 $S$ 的前 $i$ 个字符组成的字符串中，全部的 $b o r d e r$ 的数量。这两点显然是可以线性求出的。那么，每一次我们要求出 $n u m [i]$ ，我们就使用一个指针 $j$ ，不断地跳 $f a i l_{j}$ 直到 $j ⩽ ⌊ \frac{i}{2} ⌋$ 位置，最后 $n u m [i] = d p_{j}$ 。但是这个做法在全部都是 $a$ 的字符串中会退化成 $O (n^{2})$ 。我们考虑两种优化。

倍增

因为全部的 $f a i l$ 数组实际上会组成一颗 $f a i l$ 树。我们要一直跳 $f a i l$ 的过程其实十分的重复，所以我们使用树上倍增的方法将其压缩至 $O (n \log n)$ 。这个做法在本题不够优秀，但是具有启发性。

基于树上倍增的进一步优化

实际上，在一般的树上上述的倍增方法已经是足够优秀了，但是这个 $f a i l$ 树上有更为优秀的性质。 $f a i l_{i} < i$ 。也就是说对于树上的一条链，从根到叶子的过程中，我们倍增找到的那个节点的深度是单调的。我们可以维护一个指针扫一遍。时间复杂度 $O (n)$ 。具体实现并不用那么复杂，具体看代码:

$c o d e$

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int MAXN=1e6+10,mod=1e9+7;
int T,n,p[MAXN],f[MAXN];
string s;
signed main(){
	T=read();
	while(T--){
		cin>>s;n=s.length();
		memset(p,0,sizeof(p));
		memset(f,0,sizeof(f));
		for(int i=1;i<n;i++){
			int j=p[i];
			while(j&&s[i]!=s[j]) j=p[j];
			j+=(s[i]==s[j]);
			p[i+1]=j;
		}
		for(int i=1;i<=n;i++)
			f[i]=f[p[i]]+1;
		int ans=1,j=0;
		for(int i=1;i<n;i++){
			while(j&&s[i]!=s[j]) j=p[j];
			j+=(s[i]==s[j]);
			while(j>(i+1)/2) j=p[j];
			ans=ans*(f[j]+1)%mod; 
		}
		cout<<ans<<endl;
	}
	return 0;
}

BZOJ 1461 (Luogu Cow Patterns G)

题目描述

我们有两个字符串，一个是文本串，另一个是模式串。我们认为两个文本串相等当且仅当两个字符串离散化之后相等。希望直到模式串在文本串中出现的位置。

思路点拨

考虑 $KMP$ ，我们可以重新定义两个数相对位置相等。我们在模式串中，对于每一个元素 $b_{i}$ 找到一个最大的下标 $j$ 满足 $b_{j} ⩽ b_{i}$ 和一个最大的小标 $k$ 满足 $b_{i} ⩽ b_{i}$ $(j < i, k < i)$ 。也就是前驱后继。那么我们比较 $a_{i}$ 和 $b_{j}$ 是否相等的时候就可以通过判断前驱后继相对位置上的大小关系来比较是否相等。具体匹配的时候可以使用我们上述定义的相等来代替 $KMP$ 模板中的相等。

具体的正确性证明也十分简单，因为我们的前驱后继是在模式串的基础上定义的而不是在文本串上定义的，所以匹配的时候不会有问题。

$c o d e$

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int MAXN=1e6+10,mod=1e9+7;
int n,k,S,a[MAXN];
int b[MAXN],pre[MAXN],suc[MAXN]; 
struct node{
	int pos,val;
	bool friend operator<(const node &A,const node &B){
		if(A.val==B.val) return A.pos<B.pos;
		return A.val<B.val;
	}
};
set<node> s;
set<node>::iterator it;
bool equal_ofa(int x,int y){//比较 a[x] 和 b[y] 
	if(pre[y]){
		if(b[pre[y]]<b[y]&&a[x-(y-pre[y])]>=a[x]) return 0;
		if(b[pre[y]]==b[y]&&a[x-(y-pre[y])]!=a[x]) return 0;
	} 
	if(suc[y]){
		if(b[suc[y]]==b[y]&&a[x+(suc[y]-y)]!=a[x]) return 0;
		if(b[suc[y]]>b[y]&&a[x+(suc[y]-y)]<=a[x]) return 0;
	}
	return 1;
}
bool equal_ofb(int x,int y){//比较 b[x]和 b[y] 
	if(pre[y]){
		if(b[pre[y]]<b[y]&&b[x-(y-pre[y])]>=b[x]) return 0;
		if(b[pre[y]]==b[y]&&b[x-(y-pre[y])]!=b[x]) return 0;
	} 
	if(suc[y]){
		if(b[suc[y]]==b[y]&&b[x+(suc[y]-y)]!=b[x]) return 0;
		if(b[suc[y]]>b[y]&&b[x+(suc[y]-y)]<=b[x]) return 0;
	}
	return 1;
}
int fail[MAXN];
int id[MAXN],cnt;
signed main(){
	n=read(),k=read(),S=read();
	for(int i=1;i<=n;i++) a[i]=read();
	for(int i=1;i<=k;i++){
		b[i]=read();
		s.insert((node){i,b[i]}); 
		it=s.lower_bound((node){i,b[i]});
		it++;
		if(b[(*it).pos]>=b[i]&&(*it).pos<i) suc[i]=(*it).pos;
		--it;--it;
		if(b[(*it).pos]<=b[i]&&(*it).pos<i) pre[i]=(*it).pos;
	}
	for(int i=2;i<=k;i++){
		int j=fail[i-1];
		while(j&&!equal_ofb(i,j+1)) j=fail[j];
		j+=equal_ofb(i,j+1);
		fail[i]=j;
	}
	for(int i=1,j=0;i<=n;i++){
		while(j&&!equal_ofa(i,j+1)) j=fail[j];
		j+=equal_ofa(i,j+1);
		if(j==k){
			++cnt;
			id[cnt]=i-k+1;
			j=fail[j];
		} 
	}
	cout<<cnt<<endl;
	for(int i=1;i<=cnt;i++) cout<<id[i]<<endl;
	return 0;
}

[POI2005] SZA-Template

题目描述

你打算在纸上印一串字母。

为了完成这项工作，你决定刻一个印章。印章每使用一次，就会将印章上的所有字母印到纸上。

同一个位置的相同字符可以印多次。例如：用 aba 这个印章可以完成印制 ababa 的工作（中间的 a 被印了两次）。但是，因为印上去的东西不能被抹掉，在同一位置上印不同字符是不允许的。例如：用 aba 这个印章不可以完成印制 abcba 的工作。

因为刻印章是一个不太容易的工作，你希望印章的字符串长度尽可能小。

思路点拨

本题具体有两种做法，失配树和动态规划。这里讲述更好理解的失配树做法，想要了解动态规划做法可以看这里。

我们考虑建出失配树，然后寻找一些性质。对于一个印章，我们肯定需要在 $1$ 开头的位置印刷一次，在 $n$ 结尾的地方印刷一次，那么这个印章是 $1, 2, . . ., n - 1, n$ 的一个 $border$ 。答案返回到失配树上，就是根节点到 $n$ 的这一条路径上。我们的答案是在这条路径上合法，并且深度最小的点。

我们接着想，一个答案什么时候合法？对于一个失配树上的节点 $u$ ，我们对其子树内的节点排序。如果存在排序后两个相邻的元素 $i, j$ 有 $abs(i-j) > u$ ，那么这个 $u$ 肯定不合法。具体大家可以结合失配树的意义自行理解一下。类似于出现了一个长度大于 $u$ 的区间无法被 $1$ 到 $u$ 这个 $border$ 印刷出来。我们现在需要解决的就是如何找到这个最大的邻值。

如果我们从 $n$ 一路走到根节点，这个最大的邻值是单调不递增的，我们不好维护。但是如果我们是从根节点走到 $n$ ，那么添加节点机会变成添加节点，这个最大邻值也就是单调不递减的。我们可以使用一个双向链表每次 $O (1)$ 维护。总体时间复杂度 $O (n)$ 。

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int MAXN=5e5+10,mod=1e9+7;
int n,fail[MAXN];
string s;
int temp[MAXN],top;
int pre[MAXN],suc[MAXN];//双向链表 
int mx=1;//最大的邻值之差
vector<int> e[MAXN];//失配树
void erase(int x){
	if(x<1||x>n) return ;
	mx=max(mx,suc[x]-pre[x]);
	suc[pre[x]]=suc[x];
	pre[suc[x]]=pre[x];
}
void bfs(int f,int v){
	queue<int> q;
	q.push(f);
	while(!q.empty()){
		int x=q.front();
		q.pop();
		if(x==v) continue;
		erase(x);
		for(int i=0;i<e[x].size();i++){
			int to=e[x][i];
			q.push(to);
		}
	}
}
signed main(){
	cin>>s;n=s.length();
	s='0'+s;
	for(int i=2,j=0;i<=n;i++){
		while(j&&s[i]!=s[j+1]) j=fail[j];
		j+=(s[i]==s[j+1]);
		fail[i]=j;
	}//KMP
	for(int i=n;i;i=fail[i]) temp[++top]=i;//此时temp中失是降序的
	for(int i=1;i<=n;i++){
		pre[i]=i-1,suc[i]=i+1;
		e[fail[i]].push_back(i);
	}//树根为0
	for(int i=top;i;i--){
		bfs(temp[i+1],temp[i]);
		if(mx<=temp[i]){
			cout<<temp[i];
			return 0;
		}
	}
	cout<<n;
	return 0;
}

[BZOJ 2601] Country

题目描述

有 $n (n ⩽ 26)$ 个字符串变量。每一个字符串变量可以包含小写字母，也可以包含其他的字符串变量（用大写字母表示）。例如：
$A = g r e a t g l o r y c o r r e c t, B = x x, C = l e a d u s g o, D = A B C$ 。
我们保证这些字符串的定义是无环的。现在给定了一个小写字母组成的模式串，问其在某个字符串变量中出现的次数。字符串变量的长度和模式串长度单个不超过 $100$ 。

思路点拨

当一个字符串变量只有小写字母时，我们只需要做 $KMP$ 的板子就可以了。但是当我们出现的字符串的递归定义式，两个字符串之间可能产生新的满足条件的模式串。例如 $A = a b, B = A A$ ,模式串是 $b a$ 。
那么两个 $A$ 之间就多出现的了一个模式串。怎么将两个字符串变量接起来呢？我发现，在我们处理完第一个字符串变量之后，会留下一个 $f a i l$ 指针，那么第二个字符串变量就可以在这个指针的基础上继续匹配就行了。这个题目中的递归关系需要我们多次调用某一个字符串变量的情况，我们考虑使用动态规划：

定义状态 $f_{i, j}$ 表示在第 $i$ 个字符串变量， $f a i l$ 指针从 $j$ 开始匹配可以匹配出多少个模式串。

定义状态 $p o s_{i, j}$ 表示在第 $i$ 个字符串变量， $f a i l$ 指针从 $j$ 开始匹配后留下的 $f a i l$ 指针。

状态转移是十分显然的。当我们在字符串变量扫到的字母是大写时，递归求解。反之我们直接 $KMP$ 。具体看代码。本题的难度不大，但是需要对 $KMP$ 算法有十分透彻的理解。如果还是不会建议重新的，仔细再学一遍 $KMP$ 。

$c o d e$

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int MAXN=1e2+10,S=30;
const int mod=10000;
int n,len[S],fail[MAXN],m;
char s[MAXN];//s1是文本串，s2是待匹配串
char c[S][MAXN],txt[MAXN];
void init(){
	scanf("%s",s+1);
	m=strlen(s+1);
	for(int i=2;i<=m;i++){
		int j=fail[i-1];
		while(j&&s[i]!=s[j+1]) j=fail[j];
		j+=(s[i]==s[j+1]);
		fail[i]=j;
	} 
}
int f[S][MAXN],pos[S][MAXN];
//f[i][j]表示在字符串 i 开始的 j 位匹配模式串的结果
//nxt[i][j]表示在字符串 i 开始的 j 位匹配模式串后的fail指针 
void dp(int i,int j){
	if(f[i][j]!=-1) return ;
	f[i][j]=0;
	int id=j;
	for(int k=1;k<=len[i];k++){
		if('A'<=c[i][k]&&c[i][k]<='Z'){//遇到大写字母，递归求解
			dp(c[i][k]-'A',id);
			f[i][j]=(f[i][j]+f[c[i][k]-'A'][id])%mod;
			id=pos[c[i][k]-'A'][id];
		}
		else{
			while(id&&c[i][k]!=s[id+1])
				id=fail[id];
			id+=(c[i][k]==s[id+1]);
			if(id==m){
				f[i][j]=(f[i][j]+1)%mod;
				id=fail[id];
			}
		}
	}
	pos[i][j]=id;
}
signed main(){
	scanf("%lld",&n);
	scanf("%s",txt);
	for(int i=0;i<n;i++){
		scanf("%s",c[i]);
		len[i]=strlen(c[i]);
		for(int j=2;j<len[i];j++)
			c[i][j-1]=c[i][j];
		len[i]-=2;
	}
	init();//预处理fail指针
	memset(f,-1,sizeof(f));
	dp(txt[0]-'A',0);
	cout<<f[txt[0]-'A'][0];
	return 0;
}

[NOIP2020] 字符串匹配

题意描述

对于一个字符串 $S$ ，题目要求他找到 $S$ 的所有具有下列形式的拆分方案数：

$S = A B C$ ， $S = A B A B C$ ， $S = A B A B \dots A B C$ ，其中 $A$ ， $B$ ， $C$ 均是非空字符串，且 $A$ 中出现奇数次的字符数量不超过 $C$ 中出现奇数次的字符数量。

更具体地，我们可以定义 $A B$ 表示两个字符串 $A$ ， $B$ 相连接，例如 $A = aab$ ， $B = ab$ ，则 $A B = aabab$ 。

并递归地定义 $A^{1} = A$ ， $A^{n} = A^{n - 1} A$ （ $n \geq 2$ 且为正整数）。例如 $A = abb$ ，则 $A^{3} = abbabbabb$ 。

则小 C 的习题是求 $S = {(A B)}^{i} C$ 的方案数，其中 $F (A) \leq F (C)$ ， $F (S)$ 表示字符串 $S$ 中出现奇数次的字符的数量。两种方案不同当且仅当拆分出的 $A$ 、 $B$ 、 $C$ 中有至少一个字符串不同。

思路点拨

可以发现 $A B$ 是字符串 $S$ 的一个前缀，我们枚举一个 $A B$ ,紧接着枚举一个 $i$ ，这样我们就可以知道字符串 $C$ 。 $A B, i, C$ 均指题目所求得 $(A B)^{i} C$ 。我们就需要知道，在长度为 $| A B |$ 的前缀中，存在多少个 $A$ 满足 $f (A) ⩽ f (C)$ 。因为 $A, C$ 均是字符串的后缀，所以 $f (A)$ 和 $f (C)$ 可以预处理。那么已经知道了 $f (C)$ ,存在的 $f (A)$ 可以使用树状数组求出。

时间复杂度 $O (T n \log n \log | S |)$ ,其中 $S$ 是字符集大小。本题还是十分简单的，可以作为 $KMP$ 或者 $Hash$ 的练手题。对于这种题目，就是要选对该枚举的字符串，问题就会迎刃而解。这里给出一份使用字符串哈希实现的代码

$c o d e$

#include<bits/stdc++.h>
#define int unsigned long long
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int base=123;
const int MAXN=2e6+10,N=2e6;
int T,n,pw[MAXN]={1},h[MAXN];
char c[MAXN];
int hsh(int l,int r){
	int len=r-l+1;
	return h[r]-h[l-1]*pw[len];
}
int cnt[30],pre[MAXN],suc[MAXN];
void init(){
	memset(cnt,0,sizeof(cnt));
	int sum=0;
	for(int i=1;i<=n;i++){
		if(cnt[c[i]-'a']&1) sum--;
		else sum++;
		cnt[c[i]-'a']++;
		pre[i]=sum;
	}
	sum=0;
	memset(cnt,0,sizeof(cnt));
	for(int i=n;i;i--){
		if(cnt[c[i]-'a']&1) sum--;
		else sum++;
		cnt[c[i]-'a']++;
		suc[i]=sum;
	}
}
int t[30],ans;
int lowbit(int x){
	return x&(-x);
}
void add(int x,int y){
	for(int i=x+1;i<=27;i+=lowbit(i))
		t[i]+=y;
}
int query(int x){
	int sum=0;
	for(int i=x+1;i;i-=lowbit(i))
		sum+=t[i];
	return sum;
}
signed main(){
	T=read();
	for(int i=1;i<=N;i++) pw[i]=pw[i-1]*base;
	while(T--){
		scanf("%s",c+1);
		n=strlen(c+1);
		for(int i=1;i<=n;i++)
			h[i]=h[i-1]*base+c[i];
		init();
		memset(t,0,sizeof(t));
		ans=0;
		for(int len=1;len<=n;len++){
			if(len-1) add(pre[len-1],1);
			for(int i=1;i+len-1<=n;i+=len){
				if(hsh(i,i+len-1)!=h[len]) break;
				if(i+len-1<n) ans+=query(suc[i+len]);
			}
		}
		cout<<ans<<endl;
	}
	return 0;
}

[NOI2011] 阿狸的打字机

题目描述

阿狸喜欢收藏各种稀奇古怪的东西，最近他淘到一台老式的打字机。打字机上只有 $28$ 个按键，分别印有 $26$ 个小写英文字母和 B、P 两个字母。经阿狸研究发现，这个打字机是这样工作的：

输入小写字母，打字机的一个凹槽中会加入这个字母(这个字母加在凹槽的最后)。
按一下印有 B 的按键，打字机凹槽中最后一个字母会消失。
按一下印有 P 的按键，打字机会在纸上打印出凹槽中现有的所有字母并换行，但凹槽中的字母不会消失。

例如，阿狸输入 aPaPBbP，纸上被打印的字符如下：

a
aa
ab

我们把纸上打印出来的字符串从 $1$ 开始顺序编号，一直到 $n$ 。打字机有一个非常有趣的功能，在打字机中暗藏一个带数字的小键盘，在小键盘上输入两个数 $(x, y)$ （其中 $1 \leq x, y \leq n$ ），打字机会显示第 $x$ 个打印的字符串在第 $y$ 个打印的字符串中出现了多少次。

思路点拨

$ACAM$ 板题。

多模式串，多文本串的字符串匹配问题，考虑 $ACAM$ 。并且，我们不难发现，题目输入的第一个字符串就是在给我们提供一个字典树，这个字典树上的节点个数是 $O (n)$ 级别的，那么我们就可以在线性的时间内建立出 $ACAM$ 的字典树和 $fail$ 树。（一定要区分，不然下面不好做）

在线做是比较难的，考虑将询问离线下来。对于一组询问 $(u, v)$ ,如果要查询 $u$ 在 $v$ 中出现的次数，我们可以将 $v$ 的所有节点染色，查询 $u$ 在 $fail$ 树上的子树染色节点数量。对于染色这一点，我们可以在字典树上进行 $dfs$ ,对于每一个遍历的节点，将 $fail$ 树上的节点染色即可。可以使用树状数组实现。

代买实现比较简单，总体时间复杂度是 $O (n \log n)$ 。

#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int MAXN=1e5+10;
string s;
int n;
int pos[MAXN],trie[MAXN][26],tot;
vector<int> G[MAXN];//字典树 
struct node{
	int fail,sum,dad;
}t[MAXN];
struct problem{
	int u,v,id;//u在v中出现了多少次 
	//id是问题编号 
};
int ans[MAXN];
vector<problem> pb[MAXN];//存储的问题
vector<int> e[MAXN];//fail树
void init(){
	int rot=0,cnt=0;
	for(int i=0;i<s.length();i++){
		if('a'<=s[i]&&s[i]<='z'){
			char c=s[i]-'a';
			if(!trie[rot][c]){
				trie[rot][c]=++tot;
				G[rot].push_back(tot);
			}
			t[trie[rot][c]].dad=rot;
			rot=trie[rot][c];
		}
		else if(s[i]=='P'){
			t[rot].sum++;
			pos[++cnt]=rot;
		} 
		else rot=t[rot].dad;
	}
}
queue<int> q;
void build(){
	for(int i=0;i<26;i++)
		if(trie[0][i])
			q.push(trie[0][i]);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<26;i++){
			int v=trie[u][i];
			if(v){
				t[v].fail=trie[t[u].fail][i];
				q.push(v);
			}
			else trie[u][i]=trie[t[u].fail][i];
		}
	}
	for(int i=1;i<=tot;i++)
		e[t[i].fail].push_back(i);
}
int res,dfn[MAXN],siz[MAXN];
void dfs1(int x){
	dfn[x]=++res;
	siz[x]=1;
	for(int i=0;i<e[x].size();i++){
		int to=e[x][i];
		dfs1(to);
		siz[x]+=siz[to];
	}
}
int bit[MAXN];
int lowbit(int x){
	return x&(-x);
}
void add(int x,int y){
	for(int i=x;i<=res;i+=lowbit(i))
		bit[i]+=y;
}
int query(int x){
	int cnt=0;
	for(int i=x;i;i-=lowbit(i))
		cnt+=bit[i];
	return cnt;
}
void dfs2(int x){
	add(dfn[x],1);
	for(int i=0;i<pb[x].size();i++){
		int v=pos[pb[x][i].u];
		ans[pb[x][i].id]=query(dfn[v]+siz[v]-1)-query(dfn[v]-1);
	}
	for(int i=0;i<G[x].size();i++){
		int to=G[x][i];
		dfs2(to);
	}
	add(dfn[x],-1);
}
signed main(){
	cin>>s;
	init();//建立字典树
	build();
	dfs1(0);
	n=read();
	for(int i=1;i<=n;i++){
		int u=read(),v=read();
		pb[pos[v]].push_back((problem){u,v,i});
	}
	dfs2(0);//这是在字典树上
	for(int i=1;i<=n;i++) cout<<ans[i]<<endl;
	return 0;
}

Substrings in a String

题目描述

你需要维护一个文本串，支持如下操作：

将文本串的第 $i$ 个字符变成 $c h$ 。
给定一个模式串，查询其在文本串的 $[l, r]$ 中出现的次数。

$n, \sum | S | ⩽ 1 e 5$

思路点拨

我们直接bitset。

#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int MAXN=1e5+10;
char c[MAXN];
int n,q;
bitset<MAXN> temp;
bitset<MAXN> pos[26];
signed main(){
	scanf("%s",c+1);
	n=strlen(c+1);
	for(int i=1;i<=n;i++)
		pos[c[i]-'a'][i]=1;
	q=read();
	while(q--){
		int opt=read();
		if(opt==1){
			int p=read();
			char ch;cin>>ch;
			pos[c[p]-'a'][p]=0;
			c[p]=ch;
			pos[c[p]-'a'][p]=1;
		}
		else{
			int l=read(),r=read();
			string s;cin>>s;
			int len=s.length();
			temp.set();
			for(int i=0;i<len;i++)
				temp=temp&(pos[s[i]-'a']>>i);
			printf("%d\n",(s.length()>r-l+1)?0:(temp>>l).count()-(temp>>(r-s.length()+2)).count());
			//[l,r] 是我需要的区间，但是我们最终维护的temp数组只记录的字符串匹配的起点 
			//所以我们令len为字符串长度，那么我们在最终的temp中只需要考虑[l,r-len+1]
			//我们先将bitset右移l，提取出[l,n],接着右移 r-len+2位，提取出我们需要的区间
			//但是当字符串的长度大于询问区间的时候，bitset中任然可能有存留(l>r-len+1) ，我们需要特判，不然WA on 25 
		}
	}
	return 0;
}

test0717

今天的模拟赛太逆天了。 $NOIP$ 模拟赛一紫三黑。
只会 $T 1$ ，无语

T1 珠宝

题目描述

有 $n$ 个物品，每一个物品有一个空间 $w_{i}$ 和一个价值 $v_{i}$ 。

你有一个空间为 $i$ 的背包，问最多可以装下多少价值的物品。

问价值 $i ⩽ K$ 时的每一个答案。

数据范围 ： $n ⩽ 1 e 6$ , $K ⩽ 5 e 4$ , $w ⩽ 300$ 。

思路点拨

我们按照一般的 $01$ 背包的思路，本题可以做到 $O (n k)$ ，严重超时。

我们比较一般的背包问题的数据规模和本题的数据规模，本题的物品数量十分庞大，但是物品的空间很小。

我们从物品的空间下手，从 $1$ 到 $300$ 枚举一个空间 $V$ 。对于每一个空间时 $V$ 的物品打包考虑。

首先，我们可以将这些物品价值降序排序，因为我们在同样的空间下总是会先选价值大的。

接下来，我们对这些物品做前缀和，保存到数组 $g_{i \times V}$ 中，表示选择 $i$ 个空间为 $V$ 的物品的价值。

转移的时候，我们发现，两个状态 $f_{i}$ 和 $f_{j}$ 会互相影响仅当 $i \mod V = j \mod V$ 。

所以我们枚举我们要转移的状态 $\mod V$ 的余数，假设他为 $z$ 。

那么我们将形如 $f_{i \times V + z}$ 的状态放在一起考虑，得到转移方程：

f_{i \times V + z} = max {f_{i \times V + z}, max {f_{j \times V + z} + g_{(i - j) \times V}}}

这个式子对我们的时间没有任何的优化，但是 $g$ 函数的增长率时单调不递增的。证明略。

所以我们的决策点有单调性，使用分治或者单调队列上二分均可通过。本题还算是比较可做的。

T2 [JOI 2020 Final] 火事

题目描述

给定一个长为 $N$ 的序列 $S_{i}$ ，刚开始为时刻 $0$ 。

定义 $t$ 时刻第 $i$ 个数为 $S_{i} (t)$ ，那么：

{\begin{cases} S_{0} (t) = 0 \\ S_{i} (0) = S_{i} \\ S_{i} (t) = max {S_{i - 1} (t - 1), S_{i} (t - 1)} \end{cases}

你将对 $Q$ 个操作进行评估，第 $j$ 个操作让时刻 $T_{j}$ 时的区间 $[L_{j}, R_{j}]$ 全部变为 $0$ 。

执行一个操作需要一定的代价，执行第 $j$ 个操作需要以下的代价：

\sum_{k = L_{j}}^{R_{j}} S_{k} (T_{j})

求每个操作需要的代价。

注意：每个操作都是独立的。

思路点拨

考虑 $S_{i} (t) = {max}_{j = i - t}^{i} {a_{i}}$ ，所以我们可以获得 $O (n^{2})$ 的暴力。

但是，当我们把 $S_{i} (t)$ 画出来之后，我们发现对于每一个数的贡献十分的有规律，呈现出一个平行四边形。例如：

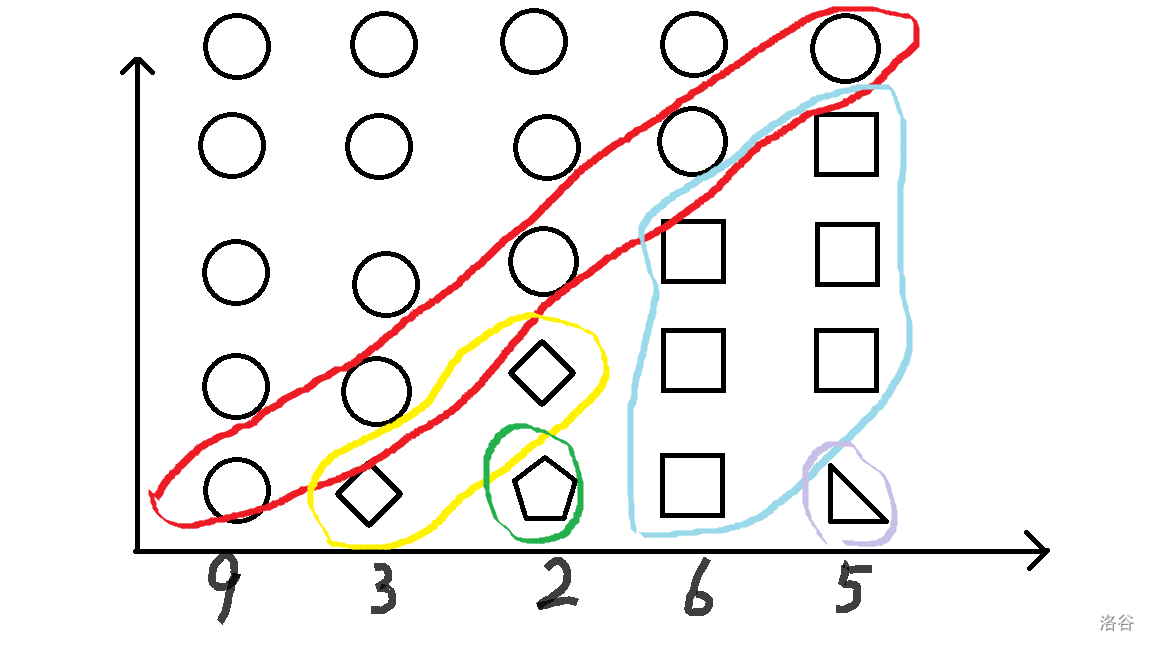
对于一个节点，我们定义 $L_{i}$ 为左边第一个大于它的数的下标， $R_{i}$ 为右边第一个 大于等于 它的数的下标。

这个平行四边形的顶点分别是 $(i, 0), (i, i - L_{i} - 1), (R_{i} - 1, R_{i} - i - 1), (R_{i} - 1, R_{i} - L_{i} - 2)$ 。

那么每一次询问就是问一个线段 $[l, r]$ 在纵坐标为 $t$ 的时候所经过的点的权值和。这个显然是可以差分简化问题的。

我们可以考虑将一个个平行四边形拆成若干个有规律的部分，使得可以更加方便计算。

一种十分简单的想法就是把一个平行四边形按照横坐标拆成一个个竖线，这样很好处理，但是全部的竖线数量过多。

我们注意到，如果按照纵坐标可以划分成一条条斜线。按照横坐标可以划分成 $R_{i} - i$ 个竖线，按照纵坐标可以划分成 $i - L_{i}$ 条斜线。

如何保证线的数量有限，可以利用笛卡尔树一个广为人知的结论 $\sum_{i} min {i - L_{i}, R_{i} - i}$ 是 $O (n \log n)$ 级别的。给出一个证明：

这个式子相当于询问笛卡尔树的每一个节点的左右儿子子树的最小值之和。

我们可以把 $min$ 换一种理解方式，把 $i$ 有左右两个儿子变换成将 $i$ 的两个儿子合并。这样取 $min$ 就可以变换成启发式合并。

每一个节点至多被合并 $\log n$ 次，所以总体是 $O (n \log n)$ 的。

接下来，我们对于横线和斜线分别考虑。

横线十分简单，将全部询问差分后离线下来就可以扫描线，比较无脑。

斜线不好搞，对于一群在同一条斜线上的点 $(x, y)$ ，我们发现随着 $x$ 加上一个 $1$ ， $y$ 也会加上一个 $1$ 。也就是说，同一条斜线上的点 $x - y$ 是一个定值。

我们将原平面直角坐标系的点 $(x, y)$ 变换成 $(x - y, y)$ 就可以将斜线转换成横线。因为在同一斜线上的点 $x - y$ 是定值。

对于斜线转换后的横线，我们可以如法炮制同样操作。在维护扫描线的时候，考虑到本题时限比较紧张，使用 $BIT$ 维护。

时间复杂度 $O (n \log^{2} n)$ 。

T3 Mousetrap

题目描述

有一个有 $n$ 个房间和 $n - 1$ 条走廊的迷宫，保证任意两个房间可以通过走廊互相到达，换句话说，这个迷宫的结构是一棵树。

一个老鼠被放进了迷宫，迷宫的管理者决定和老鼠做个游戏。

一开始，有一个房间被放置了陷阱，老鼠出现在另一个房间。老鼠可以通过走廊到达别的房间，但是会弄脏它经过的走廊。老鼠不愿意通过脏的走廊。

每个时刻，管理者可以进行一次操作：堵住一条走廊使得老鼠不能通过，或者擦干净一条走廊使得老鼠可以通过。然后老鼠会通过一条干净的并且没被堵住的走廊到达另一个房间。只有在没有这样的走廊的情况下，老鼠才不会动。一开始所有走廊都是干净的。管理者不能疏通已经被堵住的走廊。

现在管理者希望通过尽量少的操作将老鼠赶到有陷阱的房间，而老鼠则希望管理者的操作数尽量多。请计算双方都采取最优策略的情况下管理者需要的操作数量。

注意：管理者可以选择在一些时刻不操作。

对于所有的数据， $1 \leq n \leq 10^{6}$ 。

思路点拨

题目意思比较复杂，所以使用了更为清晰的原题面。

我们为了简化问题，我们将陷阱房作为数的根，这样老鼠就尽量远离根。

我们考虑这只倒霉的老鼠会怎么走。它会一头栽进一个子树然后被自己弄脏的路径困住。

那么在此时，我们伟大的管理员就可以把所有要封死的路径给堵住，最后把老鼠的路径擦干净。

我们先看看在一颗子树中，管理员的操作吧。我们定义 $f_{i}$ 表述老鼠从 $i$ 子树，和管理员斗智斗勇之后被堵在叶子然后回到 $i$ 管理员的最小步数。

我们考虑类似于数学归纳法的方式求出这个 $f_{i}$ 。也就是，在求 $f_{i}$ 的时候，我们知道 $i$ 的全部儿子的 $f_{i}$ 。

那么如果管理员无动于衷，老鼠会干什么？肯定会选一个 $f_{i}$ 最大的儿子的子树钻进去，以此拖延时间。

管理员此时是有一个步骤的，所以他可以把这个最大的 $f_{i}$ 堵住，老鼠就会走第二大的。有：

f_{i} = 2nd_max {f_{s o n}} + child

$child$ 是儿子的个数。为什么是加上 $child$ 呢？

这是因为，我们的老鼠会钻进一个第二大 $f_{i}$ 的子树，那么其他 $child-1$ 个子树的边我们肯定是要堵上的，最后还要帮老师擦干净一条边。

为什么子树内的边要堵上，有没有可能不堵边更优秀呢？不可能，因为老鼠钻进这条边就至少要擦一条边让他出来。不如花一条边堵上，多一事不如少一事。

对于 $f_{i}$ 而言，老鼠钻进了子树后被堵在的一个叶子，我们此时需要把 $f a_{i}$ 到陷阱房之间不要的岔路堵上，这个我们记录为 $g_{f a_{i}}$ 。

$g_{i}$ 怎么求呢？我们考虑从父亲继承。先放出方程：

g_{i} = g_{f a_{i}} + child - [i \neq s t]

其中 $s t$ 是起点。如果 $i$ 不是起点，那么我从起点到达 $i$ 的时候就会弄脏一条边，我们只需要擦掉 $child - 1$ 条别的边就可以了。

但是，老鼠一开始不一定会往自己的子树钻，有可能会走到别个子树钻进去。这是十分复杂的。

注意到答案可以二分，我们对于一个值 $∣$ ，判断是否可以处理。我们模拟老鼠的每一个决策，给出代码（有注释）：

bool lis[MAXN];//在s到t的路径上 
bool check(int step){
	int sum=0;//管理先手
	for(int x=s;x!=t;x=dad[x]){
		sum++;//我多一步
		int ned=0;//这是我需要的步数
		for(int i=0;i<e[x].size();i++){
			int to=e[x][i];
			if(lis[to]) continue;
			if(f[to]+g[x]<=step) continue;
			if(!sum) return 0;//步数不够，管理员速度不行
			sum--;//少了一步 
			ned++;//这是要堵上的 
		}
		step-=ned;
		if(step<0) return 0;
	} 
	return 1;
}

总体时间复杂度 $O (n \log V)$ 。

这题太逆天了！

T4 小丑

题目描述

给定一张 $n$ 个点， $m$ 条边的无向图。有 $q$ 次询问，每次询问给出一个区间 $[l, r]$ 问在删去这个区间的边后图是否是二分图。

思路点拨

我们发现删除操作十分的恶心，考虑转换成添加操作。我们可以将边的数组开两倍，对于一次删除操作 $[l, r]$ :

我们可以转换成判断 $[r + 1, l^{'} - 1]$ 是不是二分图。可以想到，对于每一个 $r$ ，我们找到一个最小的 $p o s_{r}$ 使得 $[r + 1, p o s_{r}]$ 不是二分图。

怎么求解 $p o s$ ?我们先考虑单个 $l$ ，这个 $p o s_{l}$ 显然是可以二分的。我们二分一个 $p o s_{r}$ 使用染色法或者并查集判断是不是二分图。时间复杂度 $O (n q \log n)$ 。

其实， $p o s$ 数组具有单调性，所以我们可以使用分治法优化这个二分的过程。

发现在分治的过程中，对于每一个分治的段，我们都需要花费大量时间计算并查集。但是，这个并查集可以从分治树的父亲处继承一部分。维护可持久化并查集或者可撤销并查集即可。

时间复杂度 $O (n \log^{2} n)$ 。

test0719

本场比赛难度还可以，T1和T2还是比较可做。但是题目编排三道计数我真服了。

T1 镜子

思路点拨

首先，对于一般的情况可以拆点分开考虑方向，比较简单。这不是本题的重点。

你可能会疑惑，一面添加的镜子可以用两面，这一点该如何处理？

如果一个格子放了两个镜子，又该怎么办？

其实，上述疑惑都是没有必要的。看图：

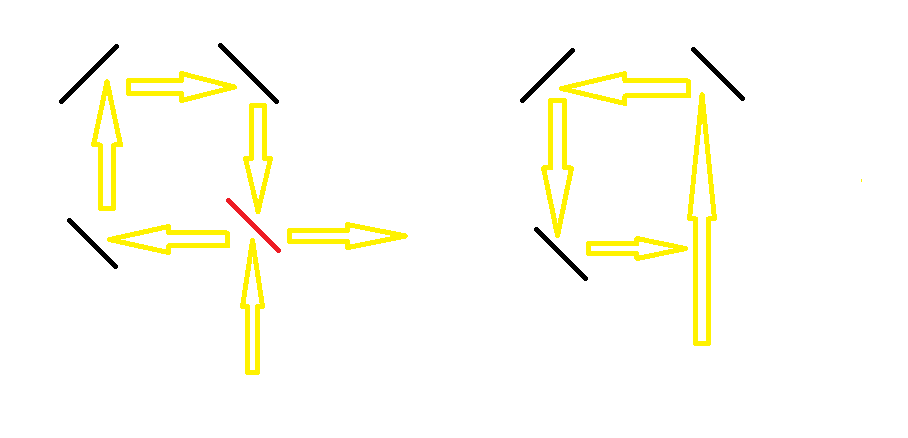
至于一个格子放两个镜子的情况，大家可以感性一下，如果这个格子被经过两个不同的方向，还是由不同方向的镜子折射的，这一定是不优秀的。我们根本不需要考虑上述两种情况。

本题时限比较紧张，考虑到边权只有 $0, 1$ ，所以 $01bfs$ 即可。

T2 [USACO20DEC] Sleeping Cows P

题目描述

Farmer John 有 $N$ （ $1 \leq N \leq 3000$ ）头各种大小的奶牛。他原本为每头奶牛量身定制了牛棚，但现在某些奶牛长大了，使得原先的牛棚大小不够用。具体地说，FJ 原来建造了 $N$ 个牛棚的大小为 $t_{1}, t_{2}, \dots, t_{N}$ ，现在奶牛的大小为 $s_{1}, s_{2}, \dots, s_{N}$ （ $1 \leq s_{i}, t_{i} \leq 10^{9}$ ）。

每天晚上，奶牛们都会按照某种方式寻找睡觉的牛棚。奶牛 $i$ 可以睡在牛棚 $j$ 中当且仅当她的大小可以进入牛棚（ $s_{i} \leq t_{j}$ ）。每个牛棚中至多可以睡一头奶牛。

我们称奶牛与牛棚的一个匹配是极大的，当且仅当每头奶牛可以进入分配给她的牛棚，且对于每头未被分配牛棚的奶牛无法进入任何未分配的空牛棚。

计算极大的匹配的数量模 $10^{9} + 7$ 的结果。

思路点拨

我们先可以发现一些显然的事实：

本题的组合意义并不是十分明显，计数题可以考虑动态规划。
我们没有考虑给其分配牛棚的体积最小的牛也必须大于最大的未匹配牛棚，不然会不合法。

为了消除第二点事实给我们带来的繁杂的影响，我们考虑将牛和牛棚放一起排序。这个 $trick$ 十分优美。

现在我们想想我们的状态需要一些什么。

目前考虑到的下标，这是显然的。

目前待选择牛棚的牛的数量，因为牛棚会减少牛的数量，选择牛会增加牛的数量。

还有一点，我们讲到第二点事实所引出的，需要记录目前下标内的牛是否被全选。

综合下来，我们定义 $f_{i, j, k}$ 表示考虑到下标为 $i$ 的牛或者牛棚， $j$ 头牛需要牛棚， $k$ 是特殊状态。 $0$ 表示前边可以选择的牛都找到牛棚了或者待找到牛棚， $1$ 反之。

考虑转移分两类讨论——牛和牛棚：

牛的转移

目前这头牛我们可以选或者不选，对于之前就有没选择的牛的那些状态：

f_{i + 1, j, 1} + = f_{i, j, 1}, f_{i + 1, j + 1, 1} + = f_{i, j, 1}

之前的牛都选择的那些状态的转移：

f_{i + 1, j + 1, 0} + = f_{i, j, 0}, f_{i + 1, j, 1} + = f_{i, j, 0}

为什么是 $f_{i + 1, j, 1} + = f_{i, j, 0}$ ?因为我们如果不选牛的话状态 $k$ 这一维状态就改变了。

牛棚的转移

目前我们存在牛未选的话，这个牛棚必须选，比较简单，略。

如果全部的牛都选的话，这个牛棚爱选不选都可以：

f_{i + 1, j - 1, 0} + = f_{i, j, 0} \times j, f_{i + 1, j, 0} + = f_{i, j, 0}

上述的转移都是比较好理解的吧。

我们的初始状态就是 $f_{0, 0, 0} = 1$ , $f_{2 \times n, 0, 0} + f_{2 \times n, 0, 1}$ 就是答案。

时间复杂度 $O (n^{2})$ ，可以通过。

T3 [JOISC2018] 修行

题目描述

求有多少个长度为 $n$ 的排列恰好有 $k$ 个位置满足 $a_{i} > a_{i + 1}$ 。

对于 $49 %$ 的数据， $n ⩽ 3 \times 10^{3}$ ;
对于 $100 %$ 的数据， $n ⩽ 10^{5}$ 。

思路点拨

部分分

本题的 $O (n^{2})$ 暴力是显然的。考虑动态规划，因为直接做有后效性，所以改成插入制。

定义 $f_{i, j}$ 表示已经考虑了 $1$ 到 $i$ ，有 $j$ 个位置满足前面比后面大。

转移分两类讨论， $j$ 是增加还是不增加。有 $f_{i, j} = f_{i - 1, j} \times j + f_{i - 1, j - 1} \times (i - j + 1)$ ，比较好理解，这里不细细讲解。

正解

考虑容斥，令 $f_{i}$ 表示恰好有 $i$ 个位置满足前面比后面大， $g_{i}$ 表示至少有 $i$ 个位置满足前面比后面大，有：

g_{i} = \sum_{i ⩽ j} C_{j}^{i} f_{j}

二项式反演得：

f_{i} = \sum_{i ⩽ j} (- 1)^{j - i} C_{j}^{i} g_{j}

那么我们考虑 $g_{i}$ 的一般做法。其实就是盒子与球问题吧，球和盒子都是不同的，具体算的话参考囧仙的博客

g_{k} = \sum_{i = 0}^{n - k} (- 1)^{n - k - i} C_{n - k}^{i} i^{n}

我们带回一般式：

f_{k} = \sum_{k ⩽ i} (- 1)^{i - k} C_{k}^{i} g_{i}

= \sum_{k ⩽ i} (- 1)^{i - k} C_{k}^{i} \sum_{j = 0}^{n - i} (- 1)^{n - i - j} C_{n - i}^{j} j^{n}

有两个 $(- 1)^{x}$ 形式的式子十分烦躁，所以我们考虑转换枚举顺序：

= \sum_{i = 0}^{n - k} (- 1)^{n - k - i} i^{n} \sum_{k ⩽ j ⩽ n - j} C_{n - j}^{i} C_{j}^{k}

前边都是快速幂的柿子，我们想后边的卷积： $\sum_{k ⩽ j ⩽ n - j} C_{n - j}^{i} C_{j}^{k}$

其实它是有组合意义的，就是我们考虑将 $n + 1$ 个数划分成 $i + k + 1$ 三个部分。我们考虑枚举其中的那个断点 $j$ ,那么左边可以选择 $C_{j}^{k}$ ，右边可以选择 $C_{n + 1 - (j + 1)}^{i} = C_{n - j}^{i}$ 。

所以上述的卷积柿子就是 $C_{n + 1}^{i + k + 1}$ 。带回原柿：

f_{k} = \sum_{i = 0}^{n - k} (- 1)^{n - k - i} i^{n} C_{n + 1}^{i + k + 1}

posted @ 2023-07-26 08:43 Diavolo-Kuang 阅读(19) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 成都集训test0719

· 成都集训-test0717

· [做题笔记 #2] 数据结构

· 闲话 22.11.3

· 数据结构选讲-1 总结

阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· ollama系列01：轻松3步本地部署deepseek，普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现

公告

昵称： Diavolo-Kuang
园龄： 1年9个月
粉丝： 0
关注： 0

+加关注

2025年3月

日

一

二

三

四

五

六

Diavolo

成都集训游记

Day1

数据结构专题（金天）

Day2

Day3

题目描述

思路点拨

思路点拨

思路点拨

题目描述

思路点拨

String 专题（冯施源）

[NOI2014]动物园

题目描述

思路点拨

BZOJ 1461 (Luogu Cow Patterns G)

题目描述

思路点拨

code

[POI2005] SZA-Template

题目描述

思路点拨

[BZOJ 2601] Country

题目描述

思路点拨

code

[NOIP2020] 字符串匹配

题意描述

思路点拨

code

[NOI2011] 阿狸的打字机

题目描述

思路点拨

Substrings in a String

题目描述

思路点拨

test0717

T1 珠宝

题目描述

思路点拨

T2 [JOI 2020 Final] 火事

题目描述

思路点拨

T3 Mousetrap

题目描述

思路点拨

T4 小丑

题目描述

思路点拨

test0719

T1 镜子

思路点拨

T2 [USACO20DEC] Sleeping Cows P

题目描述

思路点拨

牛的转移

牛棚的转移

T3 [JOISC2018] 修行

题目描述

思路点拨

部分分

正解

公告

搜索

常用链接

随笔分类

随笔档案

相册

阅读排行榜

评论排行榜

最新评论

$c o d e$

$c o d e$

$c o d e$