成都集训test0719

本场比赛难度还可以，T1和T2还是比较可做。但是题目编排三道计数我真服了。

T1 镜子

思路点拨

首先，对于一般的情况可以拆点分开考虑方向，比较简单。这不是本题的重点。

你可能会疑惑，一面添加的镜子可以用两面，这一点该如何处理？

如果一个格子放了两个镜子，又该怎么办？

其实，上述疑惑都是没有必要的。看图：

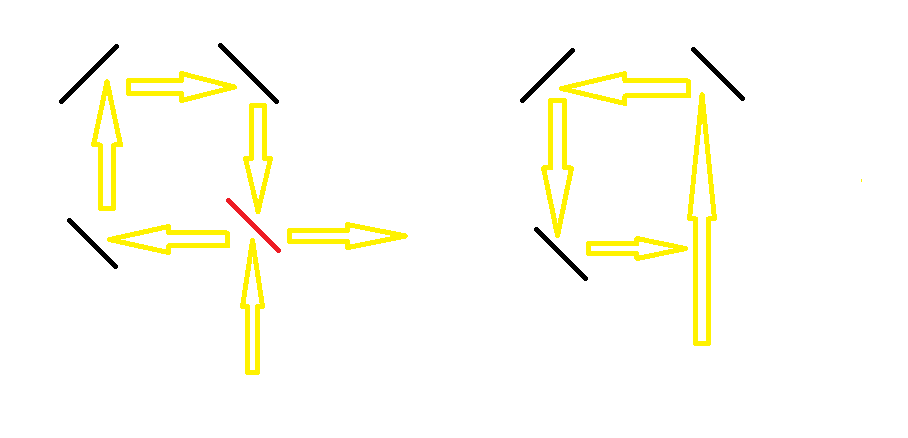
至于一个格子放两个镜子的情况，大家可以感性一下，如果这个格子被经过两个不同的方向，还是由不同方向的镜子折射的，这一定是不优秀的。我们根本不需要考虑上述两种情况。

本题时限比较紧张，考虑到边权只有 $0,1$ ，所以 $\text{01bfs}$ 即可。

T2 [USACO20DEC] Sleeping Cows P

题目描述

Farmer John 有 $N$（$1\le N\le 3000$）头各种大小的奶牛。他原本为每头奶牛量身定制了牛棚，但现在某些奶牛长大了，使得原先的牛棚大小不够用。具体地说，FJ 原来建造了 $N$ 个牛棚的大小为 $t_1,t_2,\dots ,t_N$，现在奶牛的大小为 $s_1,s_2,\dots ,s_N$（$1\le s_i,t_i\le {10}^9$）。

每天晚上，奶牛们都会按照某种方式寻找睡觉的牛棚。奶牛 $i$ 可以睡在牛棚 $j$ 中当且仅当她的大小可以进入牛棚（$s_i\le t_j$）。每个牛棚中至多可以睡一头奶牛。

我们称奶牛与牛棚的一个匹配是极大的，当且仅当每头奶牛可以进入分配给她的牛棚，且对于每头未被分配牛棚的奶牛无法进入任何未分配的空牛棚。

计算极大的匹配的数量模 ${10}^9+7$ 的结果。

思路点拨

我们先可以发现一些显然的事实：

• 本题的组合意义并不是十分明显，计数题可以考虑动态规划。

• 我们没有考虑给其分配牛棚的体积最小的牛也必须大于最大的未匹配牛棚，不然会不合法。

为了消除第二点事实给我们带来的繁杂的影响，我们考虑将牛和牛棚放一起排序。这个 $\text{trick}$ 十分优美。

现在我们想想我们的状态需要一些什么。

目前考虑到的下标，这是显然的。

目前待选择牛棚的牛的数量，因为牛棚会减少牛的数量，选择牛会增加牛的数量。

还有一点，我们讲到第二点事实所引出的，需要记录目前下标内的牛是否被全选。

综合下来，我们定义 $f_{i,j,k}$ 表示考虑到下标为 $i$ 的牛或者牛棚， $j$ 头牛需要牛棚， $k$ 是特殊状态。$0$ 表示前边可以选择的牛都找到牛棚了或者待找到牛棚， $1$ 反之。

考虑转移分两类讨论——牛和牛棚：

牛的转移

目前这头牛我们可以选或者不选，对于之前就有没选择的牛的那些状态：

$$f_{i+1,j,1}+=f_{i,j,1},f_{i+1,j+1,1}+=f_{i,j,1}$$

之前的牛都选择的那些状态的转移：

$$f_{i+1,j+1,0}+=f_{i,j,0},f_{i+1,j,1}+=f_{i,j,0}$$

为什么是 $f_{i+1,j,1}+=f_{i,j,0}$ ?因为我们如果不选牛的话状态 $k$ 这一维状态就改变了。

牛棚的转移

目前我们存在牛未选的话，这个牛棚必须选，比较简单，略。

如果全部的牛都选的话，这个牛棚爱选不选都可以：

$$f_{i+1,j-1,0}+=f_{i,j,0}\times j,f_{i+1,j,0}+=f_{i,j,0}$$

上述的转移都是比较好理解的吧。

我们的初始状态就是 $f_{0,0,0}=1$ ,$f_{2\times n,0,0}+f_{2\times n,0,1}$ 就是答案。

时间复杂度 $O(n^2)$ ，可以通过。

T3 [JOISC2018] 修行

题目描述

求有多少个长度为 $n$ 的排列恰好有 $k$ 个位置满足 $a_i>a_{i+1}$ 。

对于 $49\mathrm{\%}$ 的数据， $n⩽3\times {10}^3$ ;
对于 $100\mathrm{\%}$ 的数据，$n⩽{10}^5$ 。

思路点拨

部分分

本题的 $O(n^2)$ 暴力是显然的。考虑动态规划，因为直接做有后效性，所以改成插入制。

定义 $f_{i,j}$ 表示已经考虑了 $1$ 到 $i$ ，有 $j$ 个位置满足前面比后面大。

转移分两类讨论，$j$ 是增加还是不增加。有 $f_{i,j}=f_{i-1,j}\times j+f_{i-1,j-1}\times (i-j+1)$ ，比较好理解，这里不细细讲解。

正解

考虑容斥，令 $f_i$ 表示恰好有 $i$ 个位置满足前面比后面大， $g_i$ 表示至少有 $i$ 个位置满足前面比后面大，有：

$$g_i=\sum _{i⩽j}{C}_j^i{f}_j$$

二项式反演得：

$$f_i=\sum _{i⩽j}(-1{)}^{j-i}{C}_j^i{g}_j$$

那么我们考虑 $g_i$ 的一般做法。其实就是盒子与球问题吧，球和盒子都是不同的，具体算的话参考 囧仙的博客

$$g_k=\sum _{i=0}^{n-k}(-1{)}^{n-k-i}{C}_{n-k}^i{i}^n$$

我们带回一般式：

$$f_k=\sum _{k⩽i}(-1{)}^{i-k}{C}_k^i{g}_i$$

$$=\sum _{k⩽i}(-1{)}^{i-k}{C}_k^i\sum _{j=0}^{n-i}(-1{)}^{n-i-j}{C}_{n-i}^j{j}^n$$

有两个 $(-1{)}^x$ 形式的式子十分烦躁，所以我们考虑转换枚举顺序：

$$=\sum _{i=0}^{n-k}(-1{)}^{n-k-i}{i}^n\sum _{k⩽j⩽n-j}{C}_{n-j}^i{C}_j^k$$

前边都是快速幂的柿子，我们想后边的卷积： $\sum _{k⩽j⩽n-j}{C}_{n-j}^i{C}_j^k$

其实它是有组合意义的，就是我们考虑将 $n+1$ 个数划分成 $i+k+1$ 三个部分。我们考虑枚举其中的那个断点 $j$ ,那么左边可以选择 $C_j^k$ ，右边可以选择 $C_{n+1-(j+1)}^i=C_{n-j}^i$ 。

所以上述的卷积柿子就是 $C_{n+1}^{i+k+1}$ 。带回原柿：

$$f_k=\sum _{i=0}^{n-k}(-1{)}^{n-k-i}{i}^n{C}_{n+1}^{i+k+1}$$