拉格朗日插值
最好有小学六年级的数学水平（doge）。这篇博客的语言会比较简单通俗，大家可以先略作了解，之后通过别的文章继续深入。
基础拉格朗日插值
我们先了解最简单的拉格朗日插值可以干什么。
由小学知识可知 \(n\) 个点 \((x_i,y_i)\) 可以唯一地确定一个多项式 \(y = f(x)\)。
现在，给定这 \(n\) 个点，请你确定这个多项式。
第一眼，我们很容易想到可以使用高斯消元法在 \(O(n^3)\) 的时间内求解。但是拉格朗日插值可以做到 \(O(n^2)\) 甚至 \(O(n \log^2 n)\) 。我们这里讲解 \(O(n^2)\) 的插值。
为了举个例子，我们需要对以下四个点求出函数值：
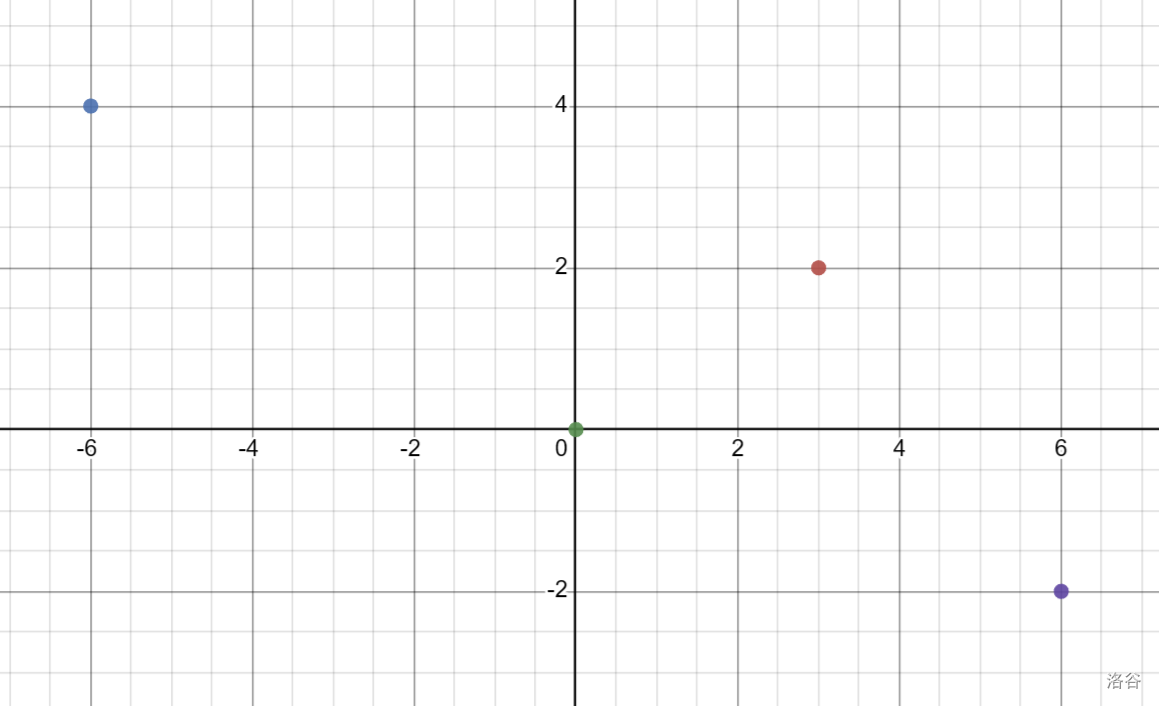
我们考虑构造 \(4\) 个基函数，期中，第 \(i\) 个基函数需要满足对于第 \(i\) 个点，函数值为 \(1\) ，其余点，函数值都为 \(0\) 。怎么构造这个基函数呢？我们拿第一个点 \((-6,4)\) 来说，如果第三个点 \((3 2)\) 要在 \(x=3\) 时 \(y=0\) ,那么我们可以为这个基函数构造 \((x-3)\) 项，这样子就会一定满足条件。我们很容易构造出基函数 \(f_1\) :
我们对于 \(x=-6\) 时需求 \(f_1(x)=1\) ，那么有：
所以有：
类似的，我们可以得到另外的基函数 \(f_2,f_3,f_4\) 。但是这样我们怎么得到最终的函数呢？
因为这个函数时一定满足我们需求的，对于给定的 \(n\) 个点之一的 \((x_i,y_i)\) ,它只有在循环到 \(i\) 时， \(y_if_i(x_i)=y_i\) 有值，其余时刻按照基函数的定义都为 \(0\) 。所以这十分合理。我们可以改写成公式的形式：
贴出一份封装了 $namespace $ 的代码：
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-f;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
const int mod=998244353;
const int MAXN=2e3+10;
namespace Lagrange{
int qpow(int a,int b){
int ans=1,base=a;
while(b){
if(b&1) ans=ans*base%mod;
base=base*base%mod;
b>>=1;
}
return ans;
}
int inv(int x){
return qpow(x,mod-2);
}
int lagrange(int n,int *x,int *y,int k){
int ans=0;
for(int i=1;i<=n;i++){
int top=1,down=1;
for(int j=1;j<=n;j++){
if(j==i) continue;
top=top*((k-x[j]+mod*2)%mod)%mod;
down=down*((x[i]-x[j]+mod*2)%mod)%mod;
}
ans=(ans+y[i]*top%mod*inv(down))%mod;
}
return ans;
}
}
using namespace Lagrange;
int n,x[MAXN],y[MAXN],k;
signed main(){
n=read(),k=read();
for(int i=1;i<=n;i++) x[i]=read(),y[i]=read();
cout<<lagrange(n,x,y,k);
return 0;
}
连续点的拉格朗日插值
很多时候，我们给出的点的 \(x_i\) 是连续的，这样我们的插值是 \(O(n)\) 的。我们先拿出刚才的式子：
可以想到，后面的分母就是两个阶乘的和，分子大概也是一段连续的数的积。具体来讲，我们可以优化 \(\prod_{j=1,j \neq i} \dfrac{x-x_i}{x_i-x_j}\) 的计算。我们定义：
\(fac_i=\prod_{j=1}^i i\)
\(g_i = \prod_{j=1}^i (k-x_i)\)
\(h_i=\prod_{j=i}^n (k-x_j)\)
那么原式就可以表示为：
注意分母的奇偶性问题，当 \(n-i\) 是奇数的时候，分母取原来的相反数。
为了不让这个博客太短，我们进行一些拓展： \(\sum_{i=1}^n i^k\) 。
没错求它的取值，但是 \(n\) 很巨大， \(k\) 会小一些。我们可以做到 \(O(k)\) ，其实是因为这个式子可以被描述为一个以 \(n\) 为变量的 \(k+1\) 次多项式。我们可以先看到一些简单例子：
貌似是这么个道理，但是有没有证明呢？我们看到三种证法：
第一种流氓证法
其实关于这一个证法是我在第一次看到这个问题的时候的个人思考，发现网上目前没有看见有这种理解方法，所以讲一下。主要的思想就是，对于任意 \(k\) ，总是有方法构造一个 \(k+1\) 次多项式函数满足条件。我们设 \(f(x)=\sum_{i=1}^x i^k\) ，那么有 \(f(x+1)-f(x)=(x+1)^k\) 。我们对于 \(f(x+1)-f(x)\) 展开来看：
我们对 $(x+1)^i $ 使用二项式定理，
也就是说，对于 \(x_i\) 项，它的系数就是:
我们知道，\(f(x+1)-f(x)=(x+1)^k=\sum_{i=0}^{k} C_{k}^i x^i\) ,所以有
这就是我们需要构造的，满足条件的那对系数 \(a\) 。但是怎么说明这样一定会有构造方案呢？
首先，在上面的公式中， \(i\) 取任何值的时候， \(j=i\) 这一项会被抵消，这是显然的：
我们考虑 \(i=k\) 的时候的取值，这个取值只根 \(j>i\) 的 \(j\) 有关系，
az这个坑先放着
