P3271 [JLOI2016] 方
[JLOI2016] 方
本文同步发表于 我的博客
题目描述
上帝说,不要圆,要方,于是便有了这道题。
由于我们应该方,而且最好能够尽量方,所以上帝派我们来找正方形上帝把我们派到了一个有 \(N\) 行 \(M\) 列的方格图上,图上一共有 \((N+1)\times(M+1)\) 个格点,我们需要做的就是找出这些格点形成了多少个正方形(换句话说,正方形的四个顶点都是格点)。
但是这个问题对于我们来说太难了,因为点数太多了,所以上帝删掉了这 \((N+1)\times(M+1)\) 中的 \(K\) 个点。既然点变少了,问题也就变简单了,那么这个时候这些格点组成了多少个正方形呢?
保证 \(0 \le x \le N \le 10^6\),\(0 \le y \le M \le 10^6\),\(K \le 2000\) 且不会出现重复的格点。
思路点拨
可以看到 \(k\) 的值域是非常的小,这暗示我们可以考虑容斥。我们称被删除的点为 "坏点" ,那么答案就是:
这样子我们就可以将答案分成 \(5\) 个部分逐个击破。如果你还是想先自己思考,这里提醒一句, 正方形可以是斜着的 。(不要问我是怎么知道的,问就是 \(5\) 分)
至少包含 \(0\) 个坏点的正方形
也就是对网格图的所有正方形计数。先放出一张图:
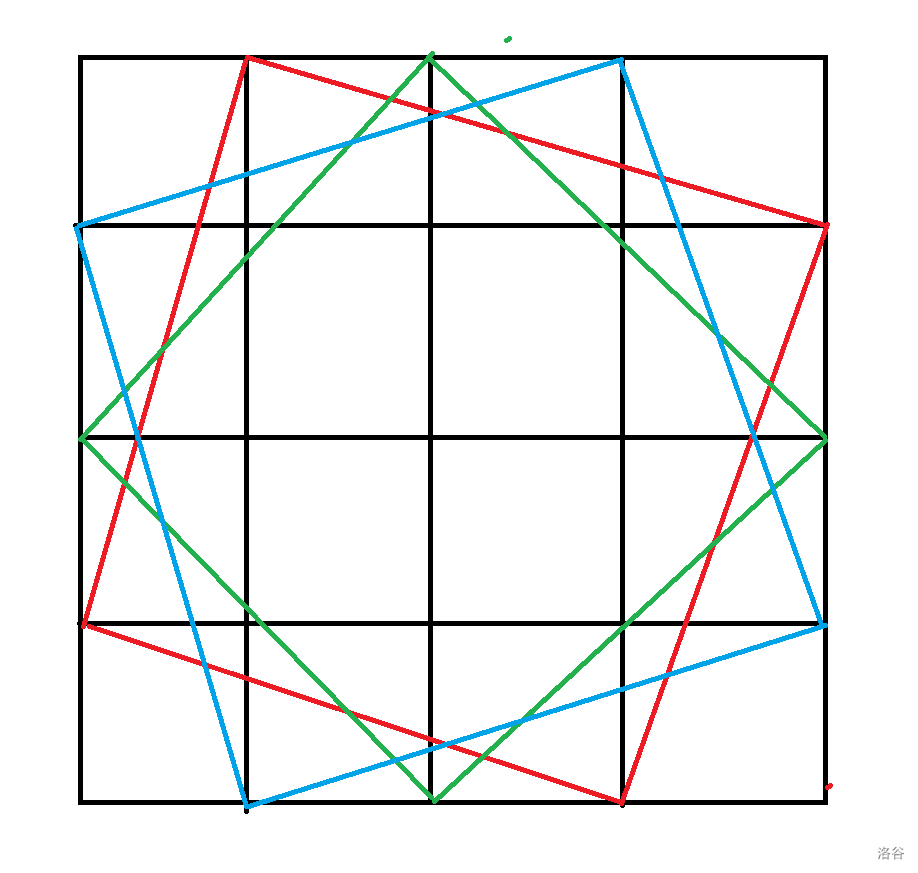
也是可以看到,一个边长为 \(i\) 的正方形,可以通过旋转得方式得到另外 \(i-1\) 个不同得正方形,加上自己就是 \(i\) 个正方形。我们就可以对于大正方形的边长计数,算出它可以旋转出多少个小的正方形,有:
这就是全部的正方形数量了。
至少包含 \(1\) 个坏点的正方形
这一点是本题的一个难点。既然至少有一个坏点,那么我们就先枚举是那个点吧。
对于每一个点,我们按照下图的方式将整个网格分成四个部分:
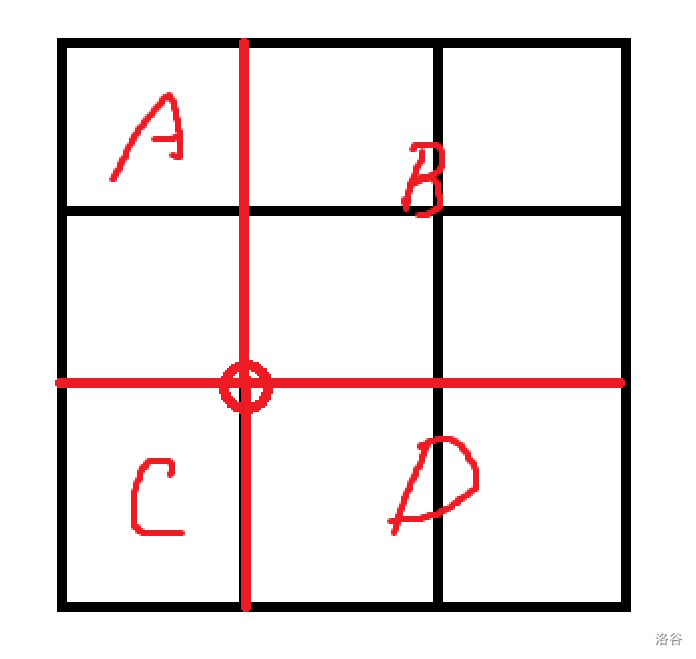
每一个坏点可以产生的贡献就是如下 \(8\) 个部分。
-
只有在 \(A\) 部分的正方形
-
只有在 \(B\) 部分的正方形
-
只有在 \(C\) 部分的正方形
-
只有在 \(D\) 部分的正方形
-
跨越了 \(AB\) 部分的正方形
-
跨域了 \(AC\) 部分的正方形
-
跨越了 \(BD\) 部分的正方形
-
跨越了 \(CD\) 部分的正方形
前四种都是十分好计数的,我们只讲后四种。我们发现,对于一个正方形,如果它跨越了两个部分,那么它一定是斜着的。如果一个斜正方形在 \(n\times m\) 网格内的,那么它有唯一个正着的大正方形包含着它,这个大正方形也在 \(n \times m\) 的网格内。可以自己画个图看一下,还是很好理解的。
接下来,我们就可以枚举那个大正方形来对斜着的正方形计数。这个正方形一定要跨越两个部分(一下按照 \(AB\) 部分的计数来讲) 。我们单纯的枚举正方形的边长(不用在意这会超时),可能会出现这个正方形在一个区域内的情况,我们可以进一步容斥,用全部的情况减去正方形在一个区域内的情况。看到下图 \(AB\) 部分,还有边长:
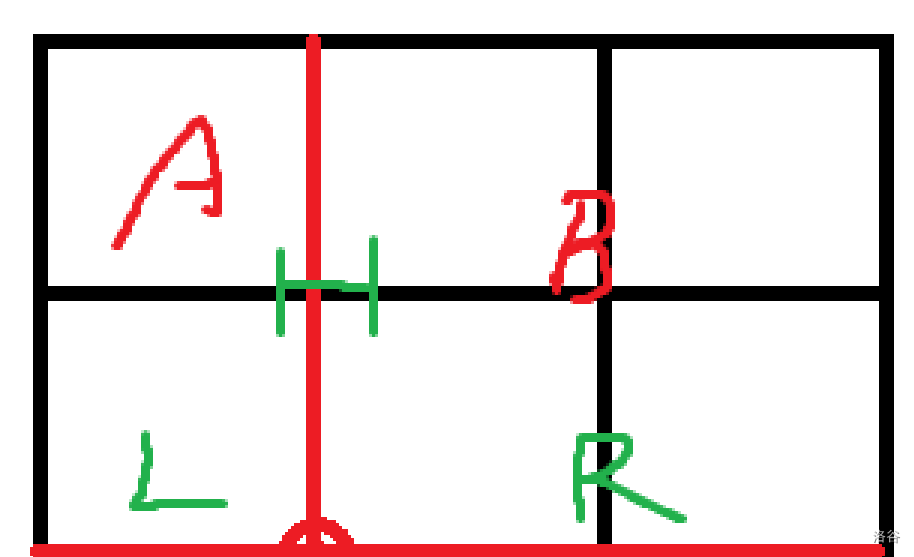
我们先讲到如何求解全部的正方形。显然我们枚举的边长 \(i\) 在 \(1\) 到 \(\min(H,L+R)\) 这个范围内。那么答案就是:
等差序列优化一下就是,首项是 \(L+R\) 末项是 \(L+R-\min(L+R,H)+1\) ,项数是 \(\min(L+R,H)\) 。就是:
接下来就是这个正方形只存在于某一个区域的情况。我们对于单个区域枚举(这部分讲述的是 \(B\) 区域),边长就是 \(R\) 。
那么这部分的答案就是
还是等差序列优化一下,首项是 \(R\) ,末项是 \(R-\min(R,H)+1\) ,项数就是 \(\min(R,H)\)
就是:
这部分我们就解决了。时间复杂度是 \(O(K)\) 。
至少包含 \(2\) 个坏点的正方形
这两个坏点我们还是考虑枚举。那么对于确定的两个点,可能的正方形只有这么几个:
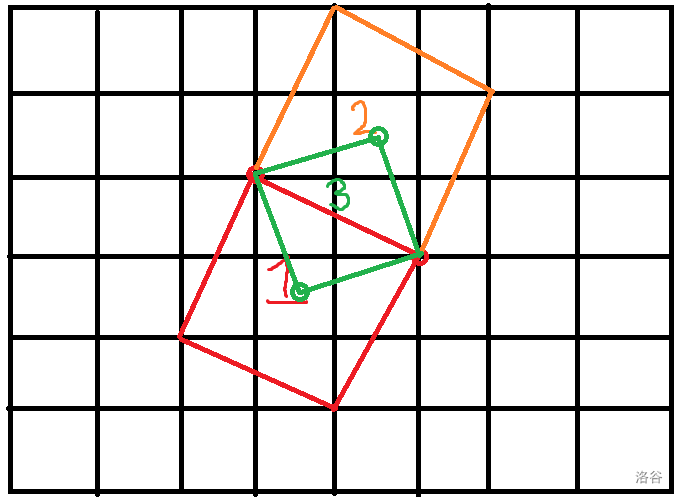
其中第三种情况并不是每时都有,初中数学判一下就可以了。怎么判,初中数学老师交过 终点坐标公式 和 三垂直模型
注意:有时候我们构造出来的正方形不一定在网格内,记得判断
至少包含 \(3\) 个坏点的正方形
类似至少包含 \(2\) 个坏点的正方形的情况,相信来做这题这一点还是会想出来。
至少包含 \(4\) 个坏点的正方形
类似至少包含 \(3\) 个坏点的正方形的情况,相信来做这题这一点还是会想出来。
总结:这题的思路还是比较好出的,但是在这道题目的坑点很多,在做题的时候要细心。
贴出一份代码,比较长,但是还算快,最优解第四:
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-f;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
const int MAXN=2e3+10,mod=1e8+7;
int n,m,k;
struct node{
int x,y;
bool friend operator<(const node &A,const node &B){
if(A.x==B.x) return A.y<B.y;
return A.x<B.x;
}
}a[MAXN];
int run0(){
int cnt=0;
for(int i=1;i<=min(n,m);i++)
cnt=(cnt+(n-i+1)*(m-i+1)%mod*i)%mod;
return cnt;
}
int h(int L,int H){
int len=min(L,H);
int ans=(L+(L-len+1))*len/2;
return ans%mod;
}
int g(int L,int R,int H){
int len=min(L+R,H);
int ans=((L+R)+(L+R-len+1))*len/2;
ans=(ans-h(L,H)-h(R,H)+mod*2)%mod;
return ans;
}
int run1(){
int cnt=0;
for(int i=1;i<=k;i++){
int H=a[i].x,L=a[i].y,R=m-a[i].y,D=n-a[i].x;
int res=min(L,H)+min(H,R)+min(R,D)+min(D,L);
cnt=(cnt+(res+g(L,R,H)+g(H,D,R)+g(R,L,D)+g(D,H,L))%mod)%mod;
}
return cnt;
}
bool check(int x,int y){
if(x<0||x>n) return 0;
if(y<0||y>m) return 0;
return 1;
}
void find(node A,node B,double &X,double &Y,int flag){
if(A.y>B.y) swap(A,B);
if(A.x>B.x){
double midx,midy;
midx=B.x+1.0*(A.x-B.x)/2;
midy=A.y+1.0*(B.y-A.y)/2;
if(flag==1){
X=midx-1.0*(midy-A.y);
Y=midy-1.0*(A.x-midx);
}
else{
X=midx+1.0*(B.y-midy);
Y=midy+1.0*(midx-B.x);
}
}
else{//A.x<B.x
double midx,midy;
midx=A.x+1.0*(B.x-A.x)/2;
midy=A.y+1.0*(B.y-A.y)/2;
if(flag==1){
X=midx-1.0*(midy-A.y);
Y=midy+1.0*(midx-A.x);
}
else{
X=midx+1.0*(B.y-midy);
Y=midy-1.0*(B.x-midx);
}
}
}
bool Integer(double x,double y){
double i=ceil(x),j=ceil(y);
if(i==x&&j==y) return 1;
return 0;
}
void get(node A,node B,node &X,node &Y,int flag){
if(A.y>B.y) swap(A,B);
if(A.x<B.x){
int midx=B.x-A.x,midy=B.y-A.y;
if(flag==1){
X.x=A.x-midy;
X.y=A.y+midx;
Y.x=B.x-midy;
Y.y=B.y+midx;
}
else{
X.x=A.x+midy;
X.y=A.y-midx;
Y.x=B.x+midy;
Y.y=B.y-midx;
}
}
else{//A.x>B.x
int midx=A.x-B.x,midy=B.y-A.y;
if(flag==1){
X.x=A.x-midy;
X.y=A.y-midx;
Y.x=B.x-midy;
Y.y=B.y-midx;
}
else{
X.x=A.x+midy;
X.y=A.y+midx;
Y.x=B.x+midy;
Y.y=B.y+midx;
}
}
}
int run2(){
int cnt=0;
for(int i=1;i<=k;i++)
for(int j=i+1;j<=k;j++){
if(i==j) continue;
double x1,x2,y1,y2;
find(a[i],a[j],x1,y1,0);
find(a[i],a[j],x2,y2,1);
if(Integer(x1,y1)&&Integer(x2,y2)&&check(x1,y1)&&check(x2,y2))
cnt++;
for(int flag=0;flag<=1;flag++){
node X,Y;
get(a[i],a[j],X,Y,flag);
if(check(X.x,X.y)&&check(Y.x,Y.y)) cnt++;
}
}
return (cnt)%mod;
}
bool truly(int x,int y){
node A;
A.x=x,A.y=y;
int id=lower_bound(a+1,a+k+1,A)-a;
if(A.x==a[id].x&&A.y==a[id].y) return 1;
return 0;
}
int run3(){
int cnt=0,cnt4=0;
for(int i=1;i<=k;i++)
for(int j=i+1;j<=k;j++){
if(i==j) continue;
double x1,x2,y1,y2;
find(a[i],a[j],x1,y1,0);
find(a[i],a[j],x2,y2,1);
if(Integer(x1,y1)&&Integer(x2,y2)&&check(x1,y1)&&check(x2,y2)){
int id1=truly((int)x1,(int)y1),id2=truly((int)x2,(int)y2);
cnt+=(id1+id2);
cnt4+=(id1&&id2);
}
for(int flag=0;flag<=1;flag++){
node X,Y;
get(a[i],a[j],X,Y,flag);
int id1=truly(X.x,X.y),id2=truly(Y.x,Y.y);
if(check(X.x,X.y)&&check(Y.x,Y.y)){
cnt+=(id1+id2);
cnt4+=(id1&&id2);
}
}
}
return ((cnt/3)%mod)-((cnt4/6)%mod);
}
signed main(){
n=read(),m=read(),k=read();
for(int i=1;i<=k;i++)
a[i].x=read(),a[i].y=read();
sort(a+1,a+k+1);
int ans=run0()-run1()+run2()-run3();
cout<<(ans+mod*10)%mod;
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号