P4515 [COCI2009-2010#6] XOR

[COCI2009-2010#6] XOR

题目描述

坐标系下有若干个等腰直角三角形，且每个等腰直角三角形的直角顶点都在左下方，两腰与坐标轴平行。被奇数个三角形覆盖的面积部分为灰色，被偶数个三角形覆盖的面积部分为白色，如下图所示。

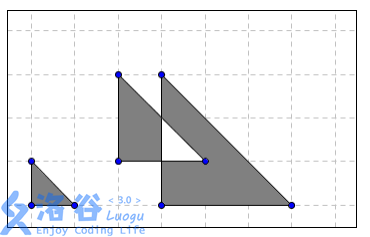
已知 \(N\)个等腰直角三角形的顶点坐标及腰长，求灰色部分面积。

\(1 \leq N \leq 10, 1 \leq X, Y, R \leq 10^6\)

思路点拨

容斥做法

这题的数据范围十分的明显, \(n=10\) ,搜索,状压,容斥什么的。再加上本题的题目配图,很容易往容斥的角度思考问题。本题具体有两种容斥做法:

第一种(不好想但是简单)

我们假设一片区域被 \(m\) 个三角形包含,这 \(m\) 个三角形共同组成了一个集合 \(S\)
有一个结论:

\[[2 \nmid m]=\sum_{T \subseteq S}(-1)^{|T|+1}2^{|T|-1} \]

这里给出一个简单的证明:

\[\sum_{T \subseteq S}(-1)^{|T|+1}2^{|T|-1} = \sum_{i=1}^{|S|}C_{m}^{i} (-1)^{i+1}2^{i-1} \]

\((-1)^{i+1}=(-1)^{i-1}\) 本质上是一样的,方便与后面的 \(2^{i-1}\) 同类项。

\[=\sum_{i=1}^{m}C_{m}^{i} (-1)^{i-1}2^{i-1}=\sum_{i=1}^m C_{m}^i (-2)^{i-1} \]

这个东东有点像 \((-2+1)^m\) 的二项式定理展开式,我们将 \((-2)^{i-1}\) 凑成 \((-2)^{i}\) , 然后二项式定理减去 \(i=0\) 的贡献就可以了。

\[=\dfrac{-1}{2}\sum_{i=1}^m C_{m}^i (-2)^{i}=\dfrac{\sum_{i=0}^m C_{m}^i (-2)^{i}-1}{-2} \]

\[=\dfrac{1-(-2+1)^{m}}{2} = [2 \nmid m] \]

OK,我们就获得了一个容斥系数。代码实现比较简单。

第二种(好想,二项式反演)

我们令 \(f(m)\) 表示 \(m\) 的容斥系数, \(g(m)=[2 \nmid m]\) 。

那么应该有 $$g(m)=\sum_{i=1}^m C_{m}^i f(i)$$

二项式反演得:

\[f(m)=\sum_{i=0}^m (-1)^{m-i} C_{m}^i g(i) \]

其实以上两种方法得到的容斥系数是一样的,至于为什么是一样的,留给读者自己思考。可以从杨辉三角或者组合恒等式的角度进行思考。

以上的两种做法都需要使用多个三角形求交,初中数学自己推一下,这里给出代码:

\(code\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int MAXN=11;
int n;
struct node{
	int x,y,w;
}a[MAXN];
int siz(node A){
	return A.w*A.w;
}
node insert(node A,node B){
	node C;
	C.x=max(A.x,B.x);
	C.y=max(A.y,B.y);
	C.w=max((int)0,min(A.x+A.y+A.w,B.x+B.y+B.w)-C.x-C.y);
	return C;
}
signed main(){
	n=read();
	for(int i=1;i<=n;i++){
		a[i].x=read(),a[i].y=read();
		a[i].w=read();
	}
	int ans=0; 
	for(int i=1;i<(1<<n);i++){
		node temp;
		int flag=0,popcount=0;
		for(int j=0;j<n;j++){
			if(!(i&(1<<j))) continue;
			popcount++;
			if(!flag){
				temp=a[j+1];
				flag=1;
			} 
			else temp=insert(temp,a[j+1]);
		}
		if(popcount&1) ans+=(siz(temp)<<popcount);
		else ans-=(siz(temp)<<popcount);
	}
	printf("%.1lf",1.0*ans/4);
	return 0;
}