二项式反演两题

例题一 [JSOI2011]分特产

题目描述

JYY 带队参加了若干场 \(\text{ACM/ICPC}\) 比赛，带回了许多土特产，要分给实验室的同学们。

JYY 想知道，把这些特产分给 \(n\) 个同学，一共有多少种不同的分法？当然，JYY 不希望任何一个同学因为没有拿到特产而感到失落，所以每个同学都必须至少分得一个特产。

例如，JYY 带来了 \(2\) 袋麻花和 \(1\) 袋包子，分给 \(A\) 和 \(B\) 两位同学，那么共有 \(4\) 种不同的
分配方法：

\(A\)：麻花， \(B\)：麻花、包子

\(A\)：麻花、麻花， \(B\)：包子

\(A\)：包子， \(B\)：麻花、麻花

\(A\)：麻花、包子， \(B\)：麻花

思路点拨

我们设 \(f(x)\) 表示至多有 \(x\) 个童鞋获得了特产的方案数。 \(g(x)\) 表示刚好有 \(x\) 个童鞋获得了特产的方案数。那么有

\[f(x)=\sum_{i=0}^x C_{x}^{i}g(i) \]

二项式反演可得：

\[g(x)=\sum_{i=0}^x (-1)^{x-i}C_{x}^if(i) \]

考虑 \(f(x)\) 的求法。我们一个个枚举每一种特产，然后插板法进行分发特产。因为元素可空，所以 \(m\) 个元素分成 \(n\) 分的方案是 \(C_{n+m-1}^{n-1}\) 。

Q:为什么特产需要一个个枚举而不是可以一起分发？
A:因为在本题中，特产是一样的，如果一起分发会造成答案重复。

\(code\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-f;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int MAXN=2e3+10,N=2e3,mod=1e9+7;
int sum[MAXN]={1},inv[MAXN]={1};
int qpow(int a,int b){
	int ans=1,base=a;
	while(b){
		if(b&1) ans=(ans*base)%mod;
		base=(base*base)%mod;
		b>>=1; 
	}
	return ans;
}
void prepare(){
	sum[0]=inv[0]=1;
	for(int i=1;i<=N;i++){
		sum[i]=sum[i-1]*i%mod;
		inv[i]=qpow(sum[i],mod-2);
	}
}
int C(int n,int m){return sum[n]*inv[m]%mod*inv[n-m]%mod;}
int n,m,a[MAXN];
signed main(){
	prepare();
	n=read(),m=read();
	int ans=0;
	for(int i=1;i<=m;i++){
		a[i]=read();
		ans+=a[i];
	}
	if(ans<n) cout<<0;
	else{
		ans=0;
		for(int i=0;i<=n;i++){
			int temp=C(n,i);
			for(int j=1;j<=m;j++)
				temp=temp*C(i+a[j]-1,i-1)%mod;
			if((n-i)&1) ans=(ans-temp+mod)%mod;
			else ans=(ans+temp)%mod;
		}
		cout<<ans;
	}
	return 0;
}

例题二 [JSOI2015]染色问题

题目描述

萌萌家有一个棋盘，这个棋盘是一个 \(n \times m\) 的矩形，分成 \(n\) 行\(m\) 列共 \(n \times m\) 个小方格。
现在萌萌和南南有 \(C\) 种不同颜色的颜料，他们希望把棋盘用这些颜料染色，并满足以下规定：

1. 棋盘的每一个小方格既可以染色（染成 \(C\) 种颜色中的一种），也可以不染色。
2. 棋盘的每一行至少有一个小方格被染色。
3. 棋盘的每一列至少有一个小方格被染色。
4. 每种颜色都在棋盘上出现至少一次。

以下是一些将 \(3 \times 3\) 棋盘染成 \(C=3\) 种颜色（红、黄、蓝）的例子（下图已更新）：

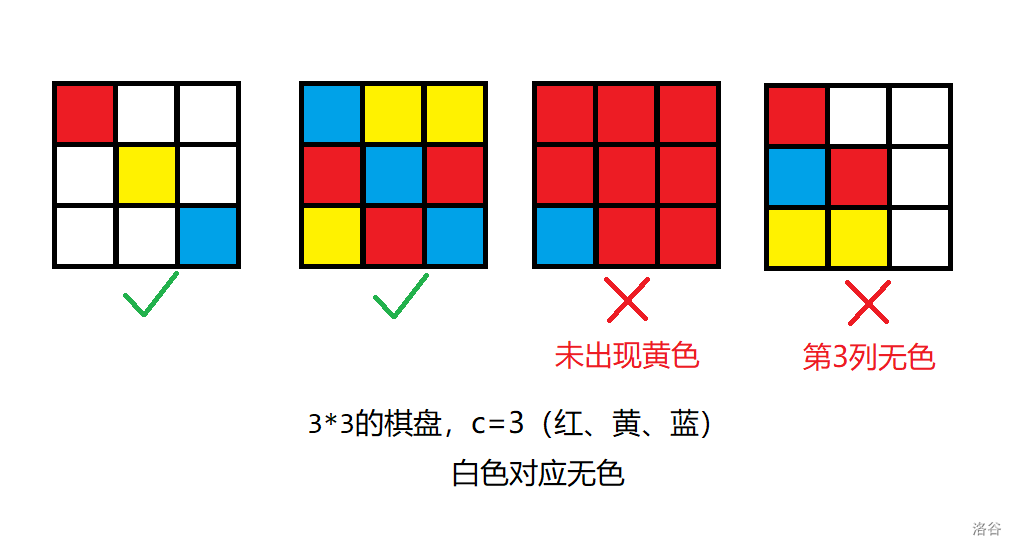
请你求出满足要求的不同的染色方案总数。只要存在一个位置的颜色不同，即认为两个染色方案是不同的。

思路点拨

二项式反演可以将 恰好有 的问题转化为 不超过 的问题 。

按照一般的想法,我们定义 \(f(x)\) 表示恰好有 \(x\) 种颜色,满足题目条件的方案数; \(g(x)\) 表示用 不超过 \(x\) 种颜色,满足题目条件的方案数。我们知道:

\[g(x)=\sum_{i=0}^{x} C_{x}^{i} f(i) \]

那么二项式反演,有:

\[f(x)=\sum_{i=0}^{x} (-1)^{x-i} C_{x}^{i} g(i) \]

考虑 \(g(x)\) 的求解。我们可以让题目条件再放宽一点。我们设 \(p(i)\) 表示用不超过 \(x\) 种颜色,在不超过 \(i\) 行满足有颜色的数量。\(q(i)\) 表示用不超过 \(x\) 种颜色,在刚好 \(i\) 行满足有颜色的数量。这依然可以二项式反演。

\[q(x) = \sum_{i=0}^{x} (-1)^{x-i} C_{x}^i p(i) \]

接下来 \(p(x)\) 该怎么求呢?一种方法是我们再对列做二项式反演,这样会变慢但是更好算。第二种方法是我们直接计算答案了。我们看看现在的约束条件,用不超过 \(k\) 种颜色,\(m\) 列中都有颜色,\(x\) 行上有颜色。(注意,这 \(x\) 行不需要组合从 \(n\) 行中选出来 \(x\) 行,不然会违背我们二项式反演成立的条件,请读者自己思考) 答案我们考虑每一列的答案,这一列上有 \(x\) 行要上色,显然是:

\[(c+1)^{x}-1 \]

减去 \(1\) 是因为全部都不上色是不合法的。最终, \(p(x)=((c+1)^{x}-1)^m\) 。

将上述公式回代进行整理可以得到以下代码:

\(code\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=401,N=400,mod=1e9+7;
int n,m,c,ans,sum[MAXN]={1},inv[MAXN]={1};
int qpow(int a,int b){
	int ans=1,base=a;
	while(b){
		if(b&1) ans=(ans*base)%mod;
		base=(base*base)%mod;
		b>>=1; 
	}
	return ans;
}
int C(int n,int m){return sum[n]*inv[m]%mod*inv[n-m]%mod;}
signed main(){
	cin>>n>>m>>c;
	for(int i=1;i<=N;i++){
		sum[i]=sum[i-1]*i%mod;
		inv[i]=qpow(sum[i],mod-2);
	} 
	for(int i=0;i<=c;i++)
		for(int j=0;j<=m;j++)
			ans=(ans+(C(c,i)*C(m,j)%mod*qpow(-1,c+m-i-j)+mod)%mod*qpow(qpow(i+1,j)-1+mod,n)%mod)%mod;
	cout<<ans;
	return 0;
}