算法理论——PLA

全称

perceptron learning algrithm

用武之地

二值分类问题，资料线性可分

算法核心（以二维平面为例）

找到一条直线W^TX=0，一边全为+1，另一边全为-1。找到了这条线（即，向量W）就得到了分类器。

如何找到这条线？

每次选取分类出错的样本点，迭代执行：W_t+1^T=W_t^T+y_n(t)X_{n(t)  （t代表第t次迭代）}

 

直观理解：改变分界线的方向，尽量在下一次预测的时候将当前预测出错的这个点出现在线的另一边。

我的问题

这里是不是默认原点就在分界线上，因为都是围绕原点进行旋转的

怎么证明PLA一定线性可分？

假设W_f就是我们要的目标分界线的向量（下面简称为目标向量吧），有：

 

但现在，我们还没有达到迭代到目标向量，对于此时，我们的X_n(t)和y_n(t)有：

 

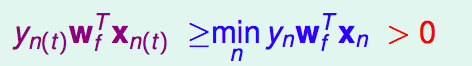
 先记住上面这个结论，下面也要用到

 

现在想要知道，我们刚得到的W_t+1^T与W_f接近程度，可以用两者的内积来表示。内积的值越大，从某种角度来说，越接近。

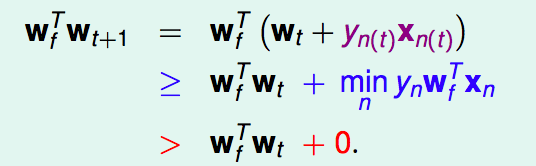    ···（1）

由此可知，通过W_t^T更新而来的W_t+1^T与比原先更接近W_f^T

但是这不能排除长度对内积的影响。

因此，下面来看看是不是能够排除长度的影响

易知：

 

 

又有：

   ···（2）

W_t^T的长度最多增加所有样本中||X_n||的最大值。这样一来，我们可以认为每次更新，其增长速度缓慢。

事实上，可以由式（1）和（2）得出以下结论：

   ···（0）

这里的constant为某常数，在后面给出。

因此，可以得出结论：对一个线性可分的数据集， 确实每次更新都使当前的分割线更靠近最理想的分割线。

另外，因为cos(Wf^T,W_T)<=1，从而得知应用PLA能够在有限的时间内得到最理想的分割线

令，接下来推导式（0），求出constant的值，并给出最大迭代次数

 

推导过程如下：

  

 

 大功告成！

PLA优点

易执行、快速、适合多维运算。

PLA缺点

1. 事实上一开始并不知道是不是线性可分
2. 也不知道到底多久会停，因为并不知道Wf^T

如果有噪声或线性不可分怎么办？

一种修正过的PLA算法：pocket algorithm

简而言之就是在每次更新之前，判断是否更新之后的错误更多，若更多就不更新，更少就更新。直到达到预定的迭代次数。