《机器学习实战》笔记——决策树（ID3）
闲来无事最近复习了一下ID3决策树算法，并凭着理解用pandas实现了一遍。对pandas更熟悉的朋友可供参考（链接如下）。相比本篇博文，更简明清晰，更适合复习用。
https://github.com/DianeSoHungry/ShallowMachineLearningCodeItOut/blob/master/ID3.ipynb
现在要介绍的是ID3决策树算法，只适用于标称型数据，不适用于数值型数据。
决策树学习算法最大的优点是，他可以自学习，在学习过程中，不需要使用者了解过多的背景知识、领域知识，只需要对训练实例进行较好的标注就可以自学习了。
建立决策树的关键在于当前状态下选择哪一个属性作为分类依据，根据不同的目标函数，有三种主要的算法：
ID3(Iterative Dichotomiser)
C4.5
CART(Classification And Regression Tree)
问题描述：
下面是一个小型的数据集，5条记录，2个特征（属性），有标签。
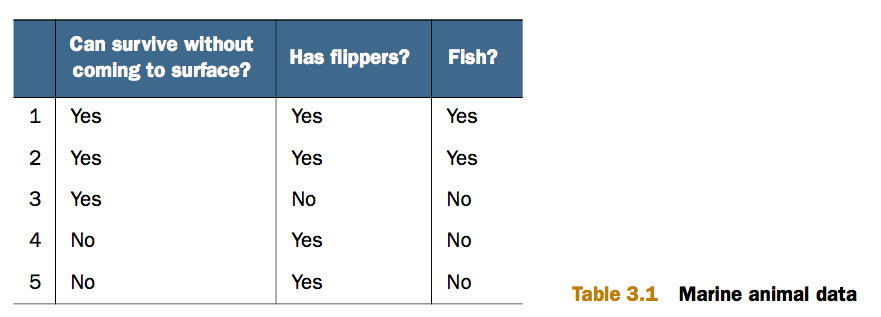
根据这个数据集，我们可以建立如下决策树（用matplotlib的注释功能画的）。
观察决策树，决策节点为特征，其分支为决策节点的各个不同取值，叶节点为预测值。
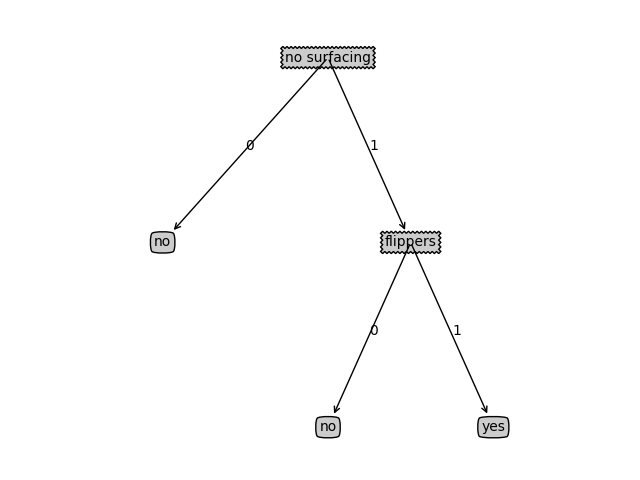
建树结束也就是建立好了一个决策树分类器，有了分类器，就可以根据这个分类器对其他的鱼进行预测了。预测准确性今天暂且不讨论。
那么如何建立这样的决策树呢？
第一步：建立决策树。
1.1 利用信息增益寻找当前最佳分类特征
想象现在你是一个判断结点，你从头顶的分支上获得了一个数据集，表中包含标签和若干属性。你现在要根据某个属性来对你接收到的数据集进行分组。到底用哪个属性来作为划分依据呢？
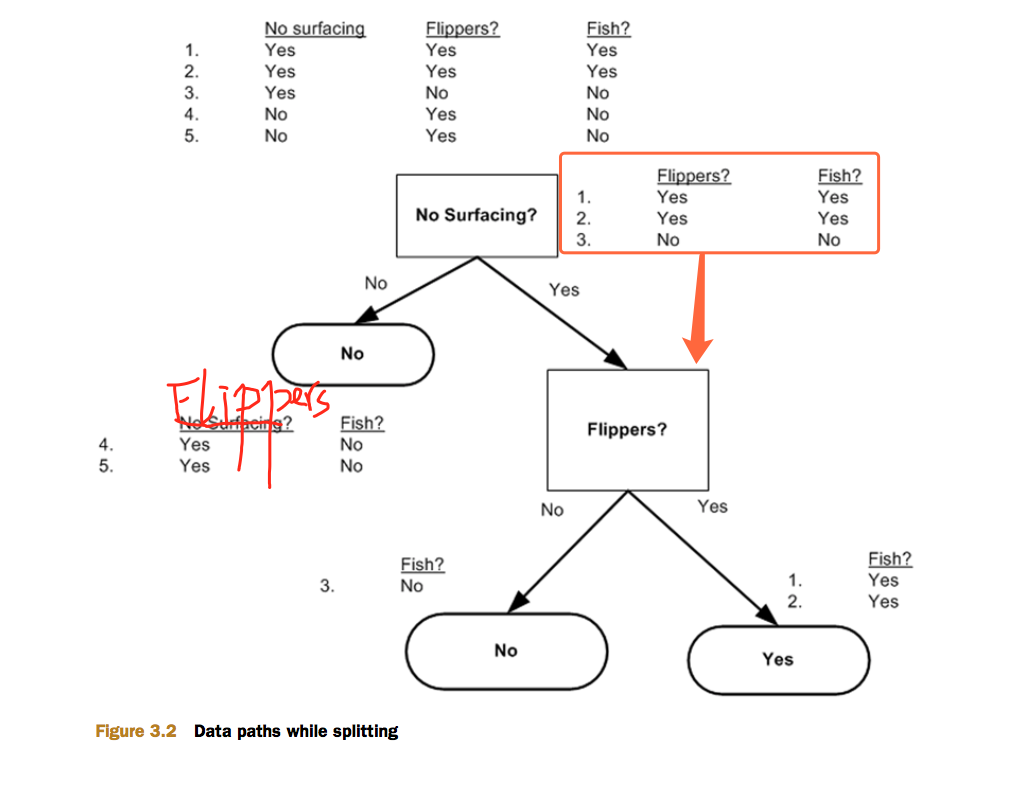
我们用信息增益来选择某个节点上用哪个特征来进行分类。
什么是信息？
如果待分类的事物可能划分在多个分类中，则每个分类xi的信息定义为：
（这里log前面应该有个负号。）
什么是香农熵？
香农熵是所有类别所有可能类别信息的期望值，即：
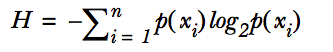
什么是信息增益？
信息增益=原香农熵-新香农熵
注意：新香农熵为按照某特征划分之后，每个分支数据集的香农熵之和。
可以这样想：香农熵相当于数据类别（标签）的混乱程度，信息增益可以衡量划分数据集前后数据（标签）向有序性发展的程度。因此，回到怎样利用信息增益寻找当前最佳分类特征的话题，假如你是一个判断节点，你拿来一个数据集，数据集里面有若干个特征，你需要从中选取一个特征，使得信息增益最大（注意：将数据集中在该特征上取值相同的记录划分到同一个分支，得到若干个分支数据集，每个分支数据集都有自己的香农熵，各个分支数据集的香农熵的期望才是新香农熵）。要找到这个特征只需要将数据集中的每个特征遍历一次，求信息增益，取获得最大信息增益的那个特征。
代码如下（其中，calcShannonEnt(dataSet)函数用来计算数据集dataSet的香农熵，splitDataSet(dataSet, axis, value)函数将数据集dataSet的第axis列中特征值为value的记录挑出来，组成分支数据集返回给函数。这两个函数后面会给出函数定义。）：
1 # 3-3 选择最好的'数据集划分方式'（特征） 2 # 一个一个地试每个特征，如果某个按照某个特征分类得到的信息增益（原香农熵-新香农熵）最大， 3 # 则选这个特征作为最佳数据集划分方式 4 def chooseBestFeatureToSplit(dataSet): 5 numFeatures = len(dataSet[0]) - 1 6 baseEntropy = calcShannonEnt(dataSet) 7 bestInfoGain = 0.0 8 bestFeature = -1 9 for i in range(numFeatures): 10 featList = [example[i] for example in dataSet] 11 uniqueVals = set(featList) 12 newEntropy = 0.0 13 for value in uniqueVals: 14 subDataSet = splitDataSet(dataSet, i, value) 15 prob = len(subDataSet) / float(len(dataSet)) 16 newEntropy += prob * calcShannonEnt(subDataSet) 17 infoGain = baseEntropy - newEntropy 18 if (infoGain > bestInfoGain): 19 bestInfoGain = infoGain 20 bestFeature = i 21 return bestFeature
calcShannonEnt(dataSet)函数代码：
1 def calcShannonEnt(dataSet): 2 numEntries = len(dataSet) # 总记录数 3 labelCounts = {} # dataSet中所有出现过的标签值为键，相应标签值出现过的次数作为值 4 for featVec in dataSet: 5 currentLabel = featVec[-1] 6 labelCounts[currentLabel] = labelCounts.get(currentLabel, 0) + 1 7 shannonEnt = 0.0 8 for key in labelCounts: 9 prob = -float(labelCounts[key])/numEntries 10 shannonEnt += prob * log(prob, 2) 11 return shannonEnt
splitDataSet(dataSet, axis, value)函数代码：
1 # 3-2 按照给定特征划分数据集（在某个特征axis上，值等于value的所有记录 2 # 组成新的数据集retDataSet，新数据集不需要axis这个特征，注意value是特征值，axis指的是特征（所在的列下标）） 3 def splitDataSet(dataSet, axis, value): 4 retDataSet = [] 5 for featVec in dataSet: 6 if featVec[axis] == value: 7 reducedFeatVec = featVec[:axis] 8 reducedFeatVec.extend(featVec[axis+1:]) 9 retDataSet.append(reducedFeatVec) 10 return retDataSet
1.2 建树
建树是一个递归的过程。
递归结束的标志（判断某节点是叶节点的标志）：
情况1. 分到该节点的数据集中，所有记录的标签列取值都一样。
或
情况2. 分到该节点的数据集中，只剩下标签列。
a. 经判断，若是叶节点，则：
对应情况1，返回数据集中第一条记录的标签值（反正所有标签值都一样）。
对应情况2，返回数据集中所有标签值中，出现次数最多的那个标签值（代码中，定义一个函数majorityCnt(classList)来实现）
b. 经判断，若不是叶节点，则：
step1. 建立一个字典，字典的键为该数据集上选出的最佳特征（划分依据）。
step2. 将具有相同特征值的记录组成新的数据集（利用splitDataSet(dataSet, axis, value)函数实现，注意期间抛弃了当前用于划分数据的特征列），对新的数据集们进行递归建树。
建树代码：
1 # 3-4 创建树的函数代码 2 # 如果非叶子结点，则以当前数据集建树，并返回该树。该树的根节点是一个字典，键为划分当前数据集的最佳特征，值为按照键值划分后各个数据集构造的树 3 # 叶子节点有两种：1.只剩没有特征时，叶子节点的返回值为所有记录中，出现次数最多的那个标签值 2.该叶子节点中，所有记录的标签相同。 4 5 def createTree(dataSet, labels): #label向量的维度为特征数，不是记录数，是不同列下标对应的特征 6 classList = [example[-1] for example in dataSet] 7 if classList.count(classList[0]) == len(classList): 8 return classList[0] 9 if len(dataSet[0]) == 1: 10 return majorityCnt(classList) 11 bestFeat = chooseBestFeatureToSplit(dataSet) 12 bestFeatLabel = labels[bestFeat] 13 myTree = {bestFeatLabel: {}} 14 del(labels[bestFeat]) 15 featValues = [example[bestFeat] for example in dataSet] 16 uniqueVals = set(featValues) 17 for value in uniqueVals: #递归建子树,若值为字典，则非叶节点，若为字符串，则为叶节点 18 myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), labels) 19 return myTree
用上面给出的数据来建立一颗决策树做示范：
在同一个程序中输入如下代码并运行：
1 def createDataSet(): 2 dataSet = [[1, 1, 'yes'], 3 [1, 1, 'yes'], 4 [1, 0, 'no'], 5 [0, 1, 'no'], 6 [0, 1, 'no']] 7 labels = ['no surfacing', 'flippers'] 8 return dataSet, labels 9 10 myDat, labels = createDataSet() 11 myTree = createTree(myDat, labels) 12 print myTree
运行结果为：
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
若利用后面画决策树的代码可以画出这颗决策树：
案例：
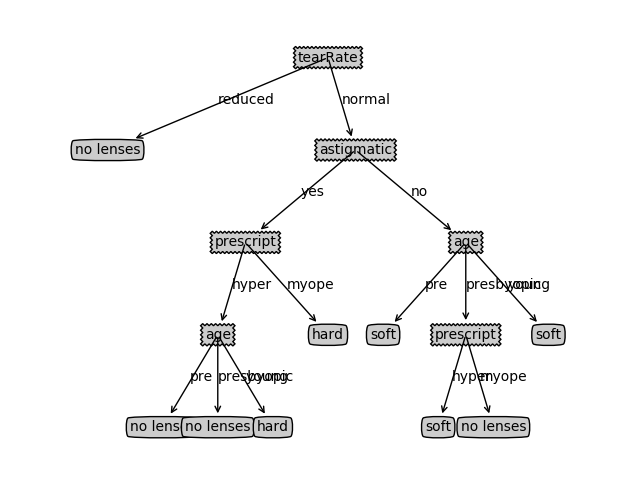
我们通过建立决策树来预测患者需要佩戴哪种隐形眼镜（soft(软材质)、hard(硬材质)、no lenses(不适合硬性眼睛）），数据集包含下面几个特征：age（年龄）, prescript（近视还是远视）, astigmatic（散光）, tearRate（眼泪清除率）
建树的结果为：
{'tearRate': {'reduced': 'no lenses', 'normal': {'astigmatic': {'yes': {'prescript': {'hyper': {'age': {'pre': 'no lenses', 'presbyopic': 'no lenses', 'young': 'hard'}}, 'myope': 'hard'}}, 'no': {'age': {'pre': 'soft', 'presbyopic': {'prescript': {'hyper': 'soft', 'myope': 'no lenses'}}, 'young': 'soft'}}}}}}
画出来是这个样子：
画决策树的代码（不讲）
涉及matplotlib.pyplot模块中的annotation的用法，点击链接进入官网学习这块内容的prerequisite。
1 # _*_coding:utf-8_*_ 2 3 # 3-7 plotTree函数 4 import matplotlib.pyplot as plt 5 6 # 定义节点和箭头格式的常量 7 decisionNode = dict(boxstyle="sawtooth", fc="0.8") 8 leafNode = dict(boxstyle="round4", fc="0.8") 9 arrow_args = dict(arrowstyle="<-") 10 11 12 def plotMidTest(cntrPt, parentPt,txtString): 13 xMid = (parentPt[0] + cntrPt[0])/2.0 14 yMid = (parentPt[1] + cntrPt[1])/2.0 15 createPlot.ax1.text(xMid, yMid, txtString) 16 17 # 绘制自身 18 # 若当前子节点不是叶子节点，递归 19 # 若当子节点为叶子节点，绘制该节点 20 def plotTree(myTree, parentPt, nodeTxt): 21 numLeafs = getNumLeafs(myTree) 22 # depth = getTreeDepth(myTree) 23 firstStr = myTree.keys()[0] 24 cntrPt = (plotTree.xoff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yoff) 25 plotMidTest(cntrPt, parentPt, nodeTxt) 26 plotNode(firstStr, cntrPt, parentPt, decisionNode) 27 secondDict = myTree[firstStr] 28 plotTree.yoff = plotTree.yoff - 1.0/plotTree.totalD 29 for key in secondDict.keys(): 30 if type(secondDict[key]).__name__=='dict': 31 plotTree(secondDict[key], cntrPt, str(key)) 32 else: 33 plotTree.xoff = plotTree.xoff + 1.0/plotTree.totalW 34 plotNode(secondDict[key], (plotTree.xoff, plotTree.yoff), cntrPt, leafNode) 35 plotMidTest((plotTree.xoff, plotTree.yoff), cntrPt, str(key)) 36 plotTree.yoff = plotTree.yoff + 1.0/plotTree.totalD 37 38 39 # figure points 40 # 画结点的模板 41 def plotNode(nodeTxt, centerPt, parentPt, nodeType): 42 createPlot.ax1.annotate(nodeTxt, # 注释的文字，（一个字符串） 43 xy=parentPt, # 被注释的地方（一个坐标） 44 xycoords='axes fraction', # xy所用的坐标系 45 xytext=centerPt, # 插入文本的地方（一个坐标） 46 textcoords='axes fraction', # xytext所用的坐标系 47 va="center", 48 ha="center", 49 bbox=nodeType, # 注释文字用的框的格式 50 arrowprops=arrow_args) # 箭头属性 51 52 53 def createPlot(inTree): 54 fig = plt.figure(1, facecolor='white') 55 fig.clf() 56 axprops = dict(xticks=[], yticks=[]) 57 createPlot.ax1 = plt.subplot(111,frameon=False, **axprops) 58 plotTree.totalW = float(getNumLeafs(inTree)) 59 plotTree.totalD = float(getTreeDepth(inTree)) 60 plotTree.xoff = -0.5/plotTree.totalW 61 plotTree.yoff = 1.0 62 63 plotTree(inTree, (0.5, 1.0),'') #树的引用作为父节点，但不画出来，所以用'' 64 plt.show() 65 66 def getNumLeafs(myTree): 67 numLeafs = 0 68 firstStr = myTree.keys()[0] 69 secondDict = myTree[firstStr] 70 for key in secondDict.keys(): 71 if type(secondDict[key]).__name__ =='dict': 72 numLeafs += getNumLeafs(secondDict[key]) 73 else: 74 numLeafs += 1 75 return numLeafs 76 77 # 子树中树高最大的那一颗的高度+1作为当前数的高度 78 def getTreeDepth(myTree): 79 maxDepth = 0 #用来记录最高子树的高度+1 80 firstStr = myTree.keys()[0] 81 secondDict = myTree[firstStr] 82 for key in secondDict.keys(): 83 if type(secondDict[key]).__name__ == 'dict': 84 thisDepth = 1 + getTreeDepth(secondDict[key]) 85 else: 86 thisDepth = 1 87 if(thisDepth > maxDepth): 88 maxDepth = thisDepth 89 return maxDepth 90 91 # 方便测试用的人造测试树 92 def retrieveTree(i): 93 listofTrees = [{'no surfacing':{0:'no',1:{'flippers':{0:'no',1:'yes'}}}}, 94 {'no surfacing':{0:'no',1:{'flippers':{0:{'head':{0:'no',1:'yes'}},1:'no'}}}} 95 ] 96 return listofTrees[i]
