数据结构和算法(4)-树
基于数组实现的结构允许我们通过下标或秩,在常数的时间内找到目标对象,并读取或更新其内容。然而,一旦需要对这类结构进行修改,那么无论是插入还是删除,都需要耗费线性的时间O(n)。
反过来,基于链表实现的结构允许我们借助引用或位置对象,在常数的时间内插入或删除元素O(1);但是为了找出居于特定次序的元素,我们不得不花费线性的时间对整个结构进行遍历查找。
树:可以结合两者的优点.
4.1 术语及性质
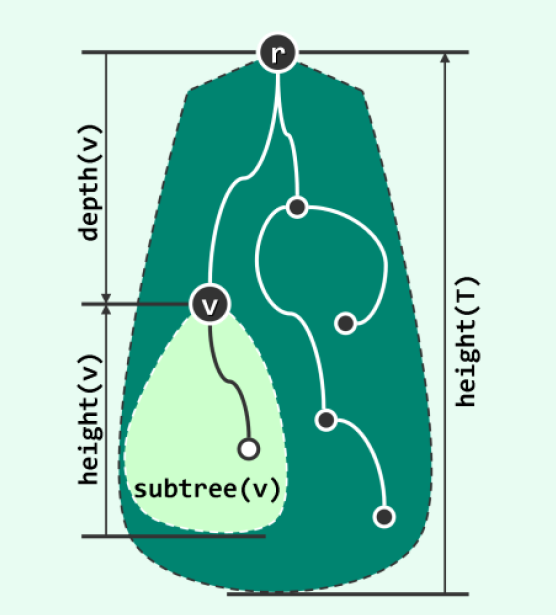
4.1.1 节点的深度、树的深度与高度
树中的元素也称作节点( Node);
在树结构中,
- 每个节点的深度都是一个非负整数;
- 树根( Root)深度为0 ;
- 对于深度为 k (k≥1)的每个节点 u,都有且仅有一个深度为 k-1 的节点 v 与之对应,称作 u 的父亲( Parent)或父节点。
- 若节点 v 是节点 u 的父亲,则 u 称作 v 的孩子( Child),并在二者之间建立一条树边( Edge);
- 树中所有节点的最大深度,称作树的深度或高度;
- 树中节点的数目,总是等于边数加一。
4.1.2 度、内部节点与外部节点
- 任一节点的孩子数目,称作它的“度”( Degree);
- 至少拥有一个孩子的节点称作“内部节点”( Internal node);没有任何孩子的节点则称作“外部节点”( External node)或“叶子”( Leaf)。一个节点是叶子,当且仅当它的度数为零。
4.1.3 路径
- 由树中 k+1 节点通过树边首尾衔接而构成的序列{ (v0, v1), (v1, v2), …, (vk-1, vk) | k ≥ 0},称作树中长度为 k 的一条路径( Path);
- 树中任何两个节点之间都存在唯一的一条路径;
- 若 v 是 u 的父亲,则 depth(v) + 1 = depth(u);
- 从树根通往任一节点的路径长度,恰好等于该节点的深度;
4.1.4 祖先、后代、子树和节点的高度
- 每个节点都是自己的“祖先”( Ancestor),也是自己的“后代”( Descendent);
- 若 v 是 u 的父节点的祖先,则 v 也是 u 的祖先;
- 若 u 的父节点是 v 的后代,则 u 也是 v 的后代;
- 任一节点 v 的深度,等于其真祖先的数目;
- 任一节点 v 的祖先,在每一深度上最多只有一个;
- 树 T 中每一节点 v 的所有后代也构成一棵树,称作 T 的“以 v 为根的子树( Subtree)”
- 若子树 v 的深度(高度)为 h,则称 v 的高度为 h,记作 height(v) = h。
- 对于叶子节点 u 的任何祖先 v,必有 depth(v) + height(v) ≥ depth(u)。
树的高度和深度:
4.1.5 共同祖先及最低共同祖先
- 在树 T 中,若节点 u 和 v 都是节点 a 的后代,则称节点 a 为节点 u 和 v 的共同祖先( Commonancestor)。
- 每一对节点至少存在一个共同祖先。
- 在一对节点 u 和 v 的所有共同祖先中,深度最大者称为它们的最低共同祖先( Lowerestcommon ancestor),记作 lca(u, v)。
- 每一对节点的最低共同祖先必存在且唯一。
4.1.6 有序树、 m 叉树
- 在树 T 中,若在每个节点的所有孩子之间都可以定义某一线性次序,则称 T 为一棵“有序树( Ordered tree)”。
- 每个内部节点均为 m 度的有序树,称作 m 叉树。
4.1.7 二叉树
- 每个节点均不超过 2 度的有序树,称作二叉树( Binary tree)。
- 不含 1 度节点的二叉树,称作真二叉树( Proper bina ry tree ),否则称作非真二叉树( Improper binary tree)。
- 在二叉树中,深度为 k 的节点不超过 2k 个。
- 高度为 h 的二叉树最多包含 2h+1-1 个节点。
- 由 n 个节点构成的二叉树,高度至少为⎣log2n⎦ .
- 在二叉树中,叶子总是比 2 度节点多一个。(等比数列求和)
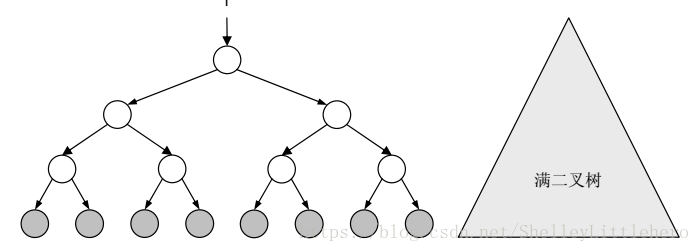
4.1.8 满二叉树与完全二叉树
- 若二叉树 T 中所有叶子的深度完全相同,则称之为满二叉树( Full binary tree)。满二叉树相当于一个完整的等腰三角形
- 高度为 h 的二叉树是满的,当且仅当它拥有 2h匹叶子、 2h+1-1 个节点
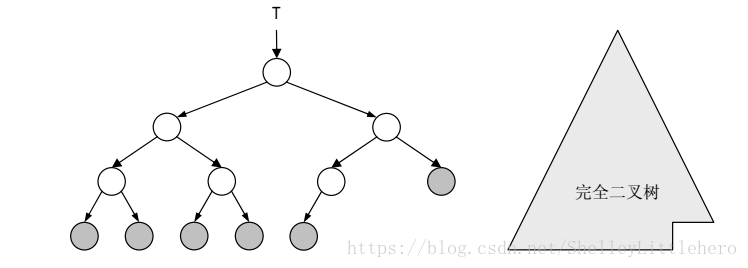
- 若在一棵满二叉树中,从最右侧起将相邻的若干匹叶子节点摘除掉,则得到的二叉树称作完全二叉树( Complete binary tree)。
- 由 n 个节点构成的完全二叉树,高度 h = ⎣log2n⎦。
- 在由固定数目的节点所组成的所有二叉树中,完全二叉树的高度最低。
4.2 树抽象数据类型及其实现
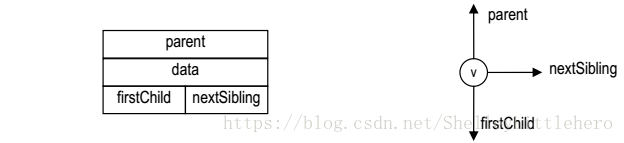
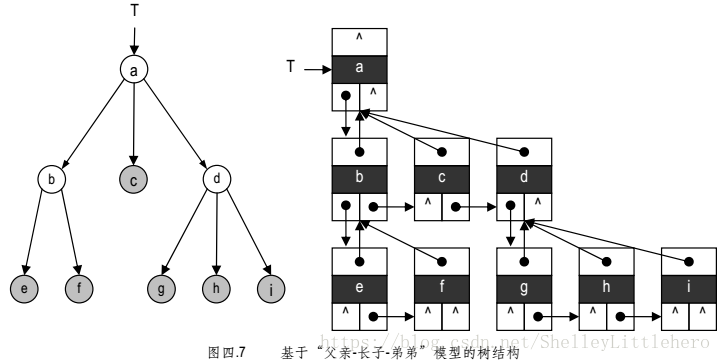
4.2.1 父亲-长子-弟弟”模型
在每个节点中除数据项外,还设有三个引用,分别指向该节点的父亲、长子和最大弟弟节点(若不存在,则为null)。
4.2.2 树 ADT
树抽象类型要支持以下的基本方法:
| 操作方法 | 功能描述 |
|---|---|
| getElement(): | 返回存放于当前节点处的对象 输入:无 输出:对象 |
| setElement(e): | 将对象 e 存入当前节点,并返回其中此前所存的内容 输入:一个对象 输出:对象 |
| getParent(): | 返回当前节点的父节点 输入:无 输出:树节点 |
| getFirstChild(): | 返回当前节点的长子 输入:无 输出:树节点 |
| getNextSibling(): | 返回当前节点的最大弟弟 输入:无 输出:树节点 |
4.2.3 树的 Java 接口
不同问题要求更新操作不同后续给出更新操作的实现;
/*
* 树ADT接口
*/
public interface Tree {
//返回当前节点中存放的对象
public Object getElem();
//将对象obj存入当前节点,并返回此前的内容
public Object setElem(Object obj);
//返回当前节点的父节点
public TreeLinkedList getParent();
//返回当前节点的长子
public TreeLinkedList getFirstChild();
//返回当前节点的最大弟弟
public TreeLinkedList getNextSibling();
//返回当前节点后代元素的数目,即以当前节点为根的子树的规模
public int getSize();
//返回当前节点的高度
public int getHeight();
//返回当前节点的深度
public int getDepth();
}
4.2.4 基于链表实现树
/*
* 基于链表实现树结构
*/
public class TreeLinkedList implements Tree {
private Object element;//树根节点
private TreeLinkedList parent, firstChild, nextSibling;//父亲、长子及最大的弟弟
//(单节点树)构造方法
public TreeLinkedList()
{ this(null, null, null, null); }
//构造方法
public TreeLinkedList(Object e, TreeLinkedList p, TreeLinkedList c, TreeLinkedList
s) {
element = e;
parent = p;
firstChild = c;
nextSibling = s;
}
/*---------- Tree接口中各方法的实现 ----------*/
//返回当前节点中存放的对象
public Object getElem()
{ return element; }
//将对象obj存入当前节点,并返回此前的内容
public Object setElem(Object obj)
{ Object bak = element; element = obj; return bak; }
//返回当前节点的父节点;对于根节点,返回null
public TreeLinkedList getParent()
{ return parent; }
//返回当前节点的长子;若没有孩子,则返回null
public TreeLinkedList getFirstChild()
{ return firstChild; }
//返回当前节点的最大弟弟;若没有弟弟,则返回null
public TreeLinkedList getNextSibling()
{ return nextSibling; }
//返回当前节点后代元素的数目,即以当前节点为根的子树的规模
public int getSize() {
int size = 1;//当前节点也是自己的后代
TreeLinkedList subtree = firstChild;//从长子开
while (null != subtree) {//依次
size += subtree.getSize();//累加
subtree = subtree.getNextSibling();//所有孩子的后代数目
}
return size;//即可得到当前节点的后代总数
}
//返回当前节点的高度
public int getHeight() {
int height = -1;
TreeLinkedList subtree = firstChild;//从长子开始
while (null != subtree) {//依次
height = Math.max(height, subtree.getHeight());//在所有孩子中取最大高度
subtree = subtree.getNextSibling();
}
return height+1;//即可得到当前节点的高度
}
//返回当前节点的深度
public int getDepth() {
int depth = 0;
TreeLinkedList p = parent;//从父亲开始
while (null != p) {//依次
depth++; p = p.getParent();//访问各个真祖先
}
return depth;//真祖先的数目,即为当前节点的深度
}
}
来源于:Java数据结构,邓俊辉


 浙公网安备 33010602011771号
浙公网安备 33010602011771号