数据结构和算法(5)-二叉树

4.4 二叉树抽象数据类型及其实现

4.4.1 二叉树 ADT

二叉树ADT支持的基本操作:

操作方法	功能描述
getElement()：	返回存放当前节点处的对象输入：无输出：对象
setElement(e)：	将对象 e 存入当前节点，并返回其中此前所存的内容输入：一个对象输出：对象
getParent()：	返getParent()：返回当前节点的父节点输入：无输出：树节点
getElement()：	返回存放当前节点处的对象输入：无输出：对象
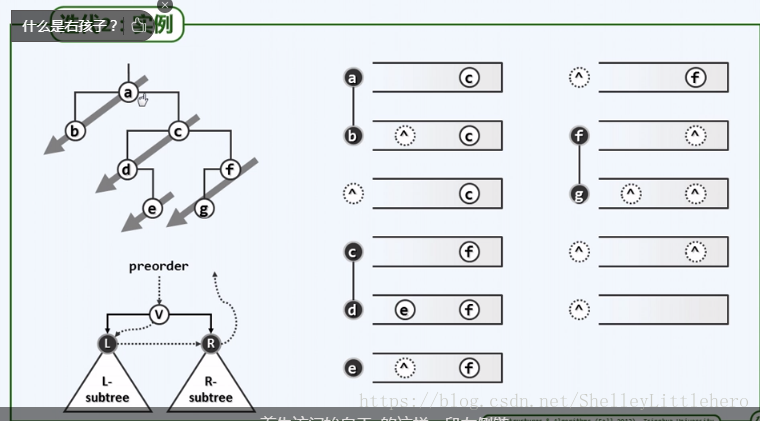
getLChild()：	返回当前节点的左孩子输入：无输出：二叉树节点
getRChild()：	返回当前节点的右孩子输入：无输出：二叉树节点

4.4.2 二叉树类的 Java 接口


public interface BinTree {
	//返回树根
	public BinTreePosition getRoot();
	//判断是否树空
	public boolean isEmpty();
	//返回树的规模（即树根的后代数目）
	public int getSize();
	//返回树（根）的高度
	public int getHeight();
	//前序遍历
	public Iterator elementsPreorder();
	//中序遍历
	public Iterator elementsInorder();
	//后序遍历
	public Iterator elementsPostorder();
	//层次遍历
	public Iterator elementsLevelorder();
}

BinTreePosition 接口:

public interface BinTreePosition extends Position {
	// 判断是否有父亲（为使代码描述简洁）
	public boolean hasParent();

	// 返回当前节点的父节点
	public BinTreePosition getParent();

	// 设置当前节点的父节点
	public void setParent(BinTreePosition p);

	// 判断是否为叶子
	public boolean isLeaf();

	// 判断是否为左孩子（为使代码描述简洁）
	public boolean isLChild();

	// 判断是否有左孩子（为使代码描述简洁）
	public boolean hasLChild();

	// 返回当前节点的左孩子
	public BinTreePosition getLChild();

	// 设置当前节点的左孩子（注意： this.lChild和c.parent都不一定为空）
	public void setLChild(BinTreePosition c);

	// 判断是否为右孩子（为使代码描述简洁）
	public boolean isRChild();

	// 判断是否有右孩子（为使代码描述简洁）
	public boolean hasRChild();

	// 返回当前节点的右孩子
	public BinTreePosition getRChild();

	// 设置当前节点的右孩子（注意： this.rChild和c.parent都不一定为空）
	public void setRChild(BinTreePosition c);

	// 返回当前节点后代元素的数目
	public int getSize();

	// 在孩子发生变化后，更新当前节点及其祖先的规模
	public void updateSize();

	// 返回当前节点的高度
	public int getHeight();

	// 在孩子发生变化后，更新当前节点及其祖先的高度
	public void updateHeight();

	// 返回当前节点的深度
	public int getDepth();

	// 在父亲发生变化后，更新当前节点及其后代的深度
	public void updateDepth();

	// 按照中序遍历的次序，找到当前节点的直接前驱
	public BinTreePosition getPrev();

	// 按照中序遍历的次序，找到当前节点的直接后继
	public BinTreePosition getSucc();

	// 断绝当前节点与其父亲的父子关系
	// 返回当前节点
	public BinTreePosition secede();

	// 将节点c作为当前节点的左孩子
	public BinTreePosition attachL(BinTreePosition c);

	// 将节点c作为当前节点的右孩子
	public BinTreePosition attachR(BinTreePosition c);

	// 前序遍历
	public Iterator elementsPreorder();
	// 中序遍历
	public Iterator elementsInorder();

	// 后序遍历
	public Iterator elementsPostorder();

	// 层次遍历
	public Iterator elementsLevelorder();
}

4.4.3 二叉树类的实现


public class BinTreeNode implements BinTreePosition {
	protected Object element;// 该节点中存放的对象
	protected BinTreePosition parent;// 父亲
	protected BinTreePosition lChild;// 左孩子
	protected BinTreePosition rChild;// 右孩子
	protected int size;// 后代数目
	protected int height;// 高度
	protected int depth;// 深度

	/**************************** 构造方法 ****************************/
	public BinTreeNode() {
		this(null, null, true, null, null);
	}

	public BinTreeNode(Object e, // 节点内容
			BinTreePosition p, // 父节点
			boolean asLChild, // 是否作为父节点的左孩子
			BinTreePosition l, // 左孩子
			BinTreePosition r)// 右孩子
	{
		size = 1;
		height = depth = 0;
		parent = lChild = rChild = null;// 初始化
		element = e;// 存放的对象
		// 建立与父亲的关系
		if (null != p)
			if (asLChild)
				p.attachL(this);
			else
				p.attachR(this);
		// 建立与孩子的关系
		if (null != l)
			attachL(l);
		if (null != r)
			attachR(r);
	}

	/**************************** Position接口方法 ********************************/
	// 返回当前节点中存放的对象
	public Object getElem() {
		return element;
	}

	// 将对象obj存入当前节点，并返回此前的内容
	public Object setElem(Object obj) {
		Object bak = element;
		element = obj;
		return bak;
	}

	/**************************** BinTreePosition接口方法 *************************/
	// 判断是否有父亲（为使代码描述简洁）
	public boolean hasParent() {
		return null != parent;
	}

	// 返回当前节点的父节点
	public BinTreePosition getParent() {
		return parent;
	}

	// 设置当前节点的父节点
	public void setParent(BinTreePosition p) {
		parent = p;
	}

	// 判断是否为叶子
	public boolean isLeaf() {
		return !hasLChild() && !hasRChild();
	}

	// 判断是否为左孩子（为使代码描述简洁）
	// 若当前节点有父亲，而且是左孩子，则返回true；否则，返回false
	public boolean isLChild() {
		return (hasParent() && this == getParent().getLChild()) ? true : false;
	}

	// 判断是否有左孩子（为使代码描述简洁）
	public boolean hasLChild() {
		return null != lChild;
	}

	// 返回当前节点的左孩子
	public BinTreePosition getLChild() {
		return lChild;
	}

	// 设置当前节点的左孩子（注意： this.lChild和c.parent都不一定为空）
	public void setLChild(BinTreePosition c) {
		lChild = c;
	}

	// 判断是否为右孩子（为使代码描述简洁）
	// 若当前节点有父亲，而且是右孩子，则返回true；否则，返回false
	public boolean isRChild() {
		return (hasParent() && this == getParent().getRChild()) ? true : false;
	}

	// 判断是否有右孩子（为使代码描述简洁）
	public boolean hasRChild() {
		return null != rChild;
	}

	// 返回当前节点的右孩子
	public BinTreePosition getRChild() {
		return rChild;
	}

	// 设置当前节点的右孩子（注意： this.rChild和c.parent都不一定为空）
	public void setRChild(BinTreePosition c) {
		rChild = c;
	}

	// 返回当前节点后代元素的数目
	public int getSize() {
		return size;
	}

	// 在孩子发生变化后，更新当前节点及其祖先的规模
	public void updateSize() {
		size = 1;// 当前节点
		if (hasLChild())
			size += getLChild().getSize();// 左子树的规模
		if (hasRChild())
			size += getRChild().getSize();// 右子树的规模
		if (hasParent())
			getParent().updateSize();// 递归更新各个真祖先的规模记录
	}

	// 返回当前节点的高度
	public int getHeight() {
		return height;
	}

	// 在孩子发生变化后，更新当前节点及其祖先的高度
	public void updateHeight() {
		height = 0;// 先假设没有左、右孩子
		if (hasLChild())
			height = Math.max(height, 1 + getLChild().getHeight());// 左孩子
		if (hasRChild())
			height = Math.max(height, 1 + getRChild().getHeight());// 右孩子
		if (hasParent())
			getParent().updateHeight();// 递归更新各个真祖先的高度记录
	}

	// 返回当前节点的深度
	public int getDepth() {
		return depth;
	}

	// 在父亲发生变化后，更新当前节点及其后代的深度
	public void updateDepth() {
		depth = hasParent() ? 1 + getParent().getDepth() : 0;// 当前节点
		if (hasLChild())
			getLChild().updateDepth();// 沿孩子引用逐层向下，
		if (hasRChild())
			getRChild().updateDepth();// 递归地更新所有后代的深度记录
	}

	// 按照中序遍历的次序，找到当前节点的直接前驱
	public BinTreePosition getPrev() {
		// 若左子树非空，则其中的最大者即为当前节点的直接前驱
		if (hasLChild())
			return findMaxDescendant(getLChild());
		// 至此，当前节点没有左孩子
		if (isRChild())
			return getParent();// 若当前节点是右孩子，则父亲即为其直接前驱
		// 至此，当前节点没有左孩子，而且是左孩子
		BinTreePosition v = this;// 从当前节点出发
		while (v.isLChild())
			v = v.getParent();// 沿左孩子链一直上升
		// 至此， v或者没有父亲，或者是父亲的右孩子
		return v.getParent();
	}

	// 按照中序遍历的次序，找到当前节点的直接后继
	public BinTreePosition getSucc() {
		// 若右子树非空，则其中的最小者即为当前节点的直接后继
		if (hasRChild())
			return findMinDescendant(getRChild());
		// 至此，当前节点没有右孩子
		if (isLChild())
			return getParent();// 若当前节点是左孩子，则父亲即为其直接后继
		// 至此，当前节点没有右孩子，而且是右孩子
		BinTreePosition v = this;// 从当前节点出发
		while (v.isRChild())
			v = v.getParent();// 沿右孩子链一直上升
		// 至此， v或者没有父亲，或者是父亲的左孩子
		return v.getParent();
	}

	// 断绝当前节点与其父亲的父子关系
	// 返回当前节点
	public BinTreePosition secede() {
		if (null != parent) {
			if (isLChild())
				parent.setLChild(null);// 切断父亲指向当前节点的引用
			else
				parent.setRChild(null);
			parent.updateSize();// 更新当前节点及其祖先的规模
			parent.updateHeight();// 更新当前节点及其祖先的高度
			parent = null;// 切断当前节点指向原父亲的引用
			updateDepth();// 更新节点及其后代节点的深度
		}
		return this;// 返回当前节点
	}

	// 将节点c作为当前节点的左孩子
	public BinTreePosition attachL(BinTreePosition c) {
		if (hasLChild())
			getLChild().secede();// 摘除当前节点原先的左孩子
		if (null != c) {
			c.secede();// c脱离原父亲
			lChild = c;
			c.setParent(this);// 确立新的父子关系
			updateSize();// 更新当前节点及其祖先的规模
			updateHeight();// 更新当前节点及其祖先的高度
			c.updateDepth();// 更新c及其后代节点的深度
		}
		return this;
	}

	// 将节点c作为当前节点的右孩子
	public BinTreePosition attachR(BinTreePosition c) {
		if (hasRChild())
			getRChild().secede();// 摘除当前节点原先的右孩子
		if (null != c) {
			c.secede();// c脱离原父亲
			rChild = c;
			c.setParent(this);// 确立新的父子关系
			updateSize();// 更新当前节点及其祖先的规模
			updateHeight();// 更新当前节点及其祖先的高度
			c.updateDepth();// 更新c及其后代节点的深度
		}
		return this;
	}

	// 前序遍历
	public Iterator elementsPreorder() {
		List list = new List_DLNode();
		preorder(list, this);
		return list.elements();
	}

	// 中序遍历
	public Iterator elementsInorder() {
		List list = new List_DLNode();
		inorder(list, this);
		return list.elements();
	}

	// 后序遍历
	public Iterator elementsPostorder() {
		List list = new List_DLNode();
		postorder(list, this);
		return list.elements();
	}

	// 层次遍历
	public Iterator elementsLevelorder() {
		List list = new List_DLNode();
		levelorder(list, this);
		return list.elements();
	}

	/**************************** 辅助方法 ****************************/
	// 在v的后代中，找出最小者
	protected static BinTreePosition findMinDescendant(BinTreePosition v) {
		if (null != v)
			while (v.hasLChild())
				v = v.getLChild();// 从v出发，沿左孩子链一直下降
		// 至此， v或者为空，或者没有左孩子
		return v;
	}

	// 在v的后代中，找出最大者
	protected static BinTreePosition findMaxDescendant(BinTreePosition v) {
		if (null != v)
			while (v.hasRChild())
				v = v.getRChild();// 从v出发，沿右孩子链一直下降
		// 至此， v或者为空，或者没有右孩子
		return v;
	}

	// 前序遍历以v为根节的（子）树
	protected static void preorder(List list, BinTreePosition v) {
		if (null == v)
			return;// 递归基：空树
		list.insertLast(v);// 访问v
		preorder(list, v.getLChild());// 遍历左子树
		preorder(list, v.getRChild());// 遍历右子树
	}

	// 中序遍历以v为根节的（子）树
	protected static void inorder(List list, BinTreePosition v) {
		if (null == v)
			return;// 递归基：空树
		inorder(list, v.getLChild());// 遍历左子树
		list.insertLast(v);// 访问v
		inorder(list, v.getRChild());// 遍历右子树
	}

	// 后序遍历以v为根节的（子）树
	protected static void postorder(List list, BinTreePosition v) {
		if (null == v)
			return;// 递归基：空树
		postorder(list, v.getLChild());// 遍历左子树
		postorder(list, v.getRChild());// 遍历右子树
		list.insertLast(v);// 访问v
	}

	// 层次遍历以v为根节的（子）树
	protected static void levelorder(List list, BinTreePosition v) {
		Queue_List Q = new Queue_List();// 空队
		Q.enqueue(v);// 根节点入队
		while (!Q.isEmpty()) {
			BinTreePosition u = (BinTreePosition) Q.dequeue();// 出队
			list.insertLast(u);// 访问v
			if (u.hasLChild())
				Q.enqueue(u.getLChild());
			if (u.hasRChild())
				Q.enqueue(u.getRChild());
		}

	}
}

二叉树类的实现

public class BinTree_LinkedList implements BinTree {

	protected BinTreePosition root;// 根节点

	/**************************** 构造函数 ****************************/
	public BinTree_LinkedList() {
		this(null);
	}

	public BinTree_LinkedList(BinTreePosition r) {
		root = r;
	}

	/**************************** BinaryTree接口方法 ****************************/
	// 返回树根
	public BinTreePosition getRoot() {
		return root;
	}

	// 判断是否树空
	public boolean isEmpty() {
		return null == root;
	}

	// 返回树的规模（即树根的后代数目）
	public int getSize() {
		return isEmpty() ? 0 : root.getSize();
	}

	// 返回树（根）的高度
	public int getHeight() {
		return isEmpty() ? -1 : root.getHeight();
	}

	// 前序遍历
	public Iterator elementsPreorder() {
		return root.elementsPreorder();
	}

	// 中序遍历
	public Iterator elementsInorder() {
		return root.elementsInorder();
	}

	// 后序遍历
	public Iterator elementsPostorder() {
		return root.elementsPostorder();
	}

	// 层次遍历
	public Iterator elementsLevelorder() {
		return root.elementsLevelorder();
	}
}

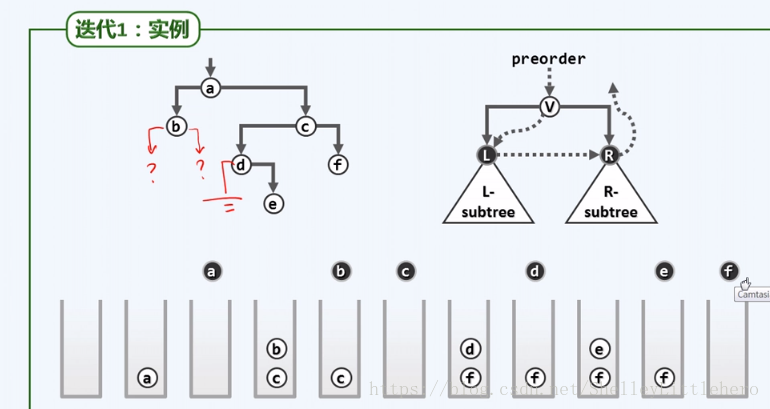
以先序遍历为例展示

在这里插入图片描述

4.5 二叉树的基本算法

4.5.1 getSize()、 getHeight()和 getDepth()

/返回当前节点后代元素的数目，即以当前节点为根的子树的规模
public int getSize() {
	int size = 1;//当前节点也是自己的后代
	TreeLinkedList subtree = firstChild;//从长子开始
	while (null != subtree) {//依次
	size += subtree.getSize();//累加
	subtree = subtree.getNextSibling();//所有孩子的后代数目
	}
	return size;//即可得到当前节点的后代总数
}
//返回当前节点的高度
public int getHeight() {
	int height = -1;
	TreeLinkedList subtree = firstChild;//从长子开始
	while (null != subtree) {//依次
	height = Math.max(height, subtree.getHeight());//在所有孩子中取最大高度
	subtree = subtree.getNextSibling();
	}
	return height+1;//即可得到当前节点的高度
}
//返回当前节点的深度
public int getDepth() {
	int depth = 0;
	TreeLinkedList p = parent;//从父亲开始
	while (null != p) {//依次
	depth++; p = p.getParent();//访问各个真祖先
	}
	return depth;//真祖先的数目，即为当前节点的深度
}

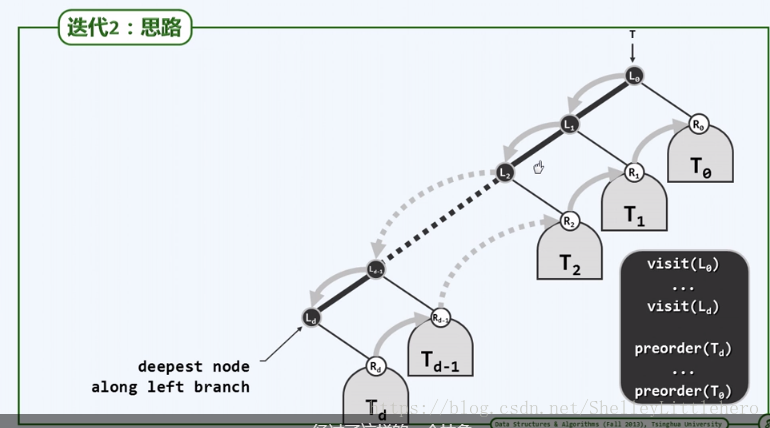
4.5.2 updateSize()

算法： updateSize(v)
输入：二叉树中任一节点v
输出：更新v的后代规模记录
{
	令size(v) = 1 + size(lc) + size(rc);//由观察结论四.13
	若v的父亲p存在，则调用updateSize(p)，递归地更新父亲的规模记录;//尾递归，可改写为迭代形式
}

4.5.3 updateHeight()

算法： updateHeight(v)
输入：二叉树中任一节点v
输出：更新v的高度记录
{
	height(v) = 0;//先假设没有左、右孩子
	若v有左孩子lc，则令： height(v) = Max(height(v), 1 + height(lc));
	若v有右孩子lc，则令： height(v) = Max(height(v), 1 + height(rc));
	若v的父亲p存在，则调用updateHeight(p)，递归地更新父亲的高度记录;
}

4.5.4 updateDepth()

算法： updateDepth(v)
输入：二叉树中任一节点v
输出：更新v的深度记录
{
	若v的父亲节点p存在，则令depth(v) = depth(p)+1;
	否则，令depth(v) = 0;
	若v的左孩子lc存在，则调用updateDepth(lc);//沿孩子引用逐层向下，
	若v的右孩子rc存在，则调用updateDepth(rc);//递归地更新所有后代的深度记录
}

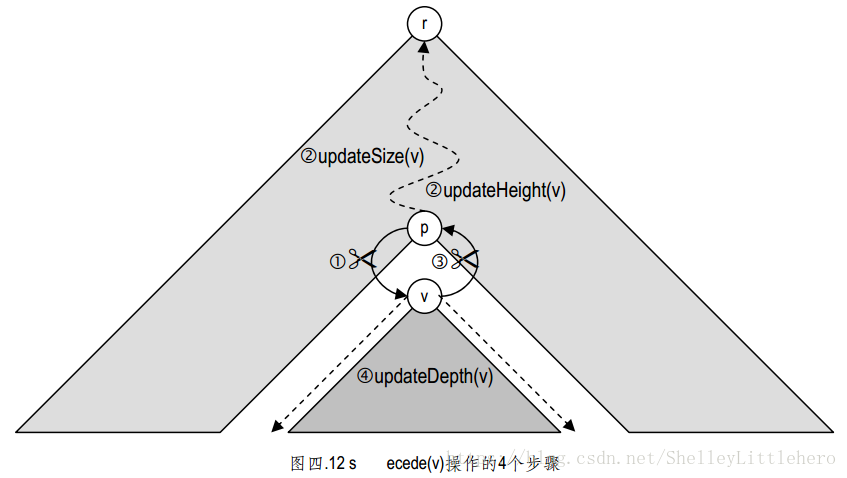
4.5.5 secede()

secede方法的功能是，将以某一节点为根的子树从母树中分离出来:
在这里插入图片描述

算法： secede(v)
输入：二叉树中任一节点v
输出：将以v为根的子树丛母树中分离出来
{
若v有父亲 {
	c 切断父亲指向v的引用;
	d 调用updateSize(v)和updateHeight(v)，更新v及其祖先的规模记录和高度记录;
	e 切断v指向父亲的引用;
	f 调用updateDepth(v)，更新v及其后代的深度记录;
	}
}

secede(v)算法的运行时间为 O(depth(v)+ size(v)+1)

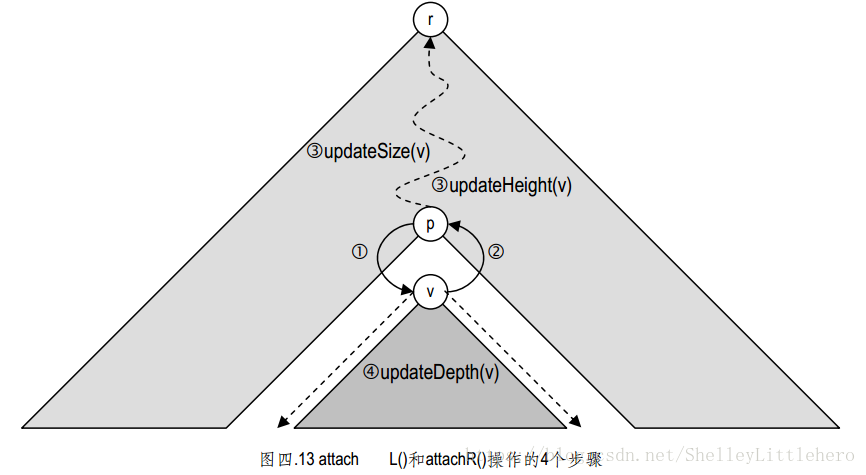
4.5.6 attachL()和 attachR()

这一对方法的功能是，将节点c作为左或右孩子与节点v联接起来;
在这里插入图片描述

算法： attachL(p, c)
输入：两个二叉树节点p与c
输出：将c作为左孩子，与p联接起来
{
	b 若p已经有左孩子lc，则首先调用secede(lc)将其摘除;
	b 调用secede(c)，使c及其后代脱离原属母树;
	cd 设置相应的引用，在p和c之间建立父子关系;
	e 调用updateSize(p)和updateHeight(p)，更新节点p及其祖先的规模和高度;
	f 调用updateDepth(c)，更新c及其后代节点的深度;
}

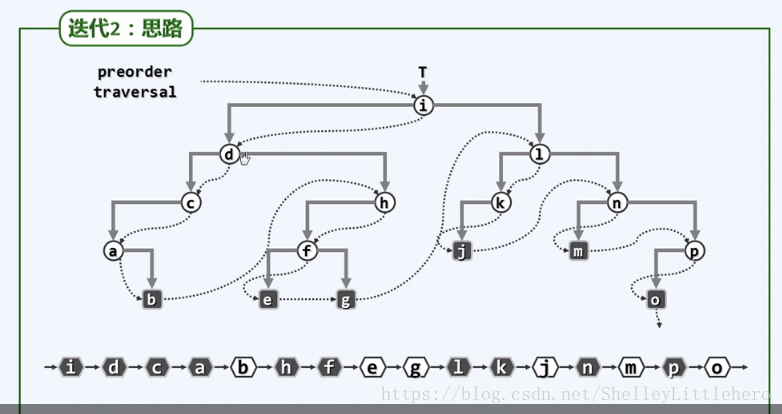
4.5.7 二叉树的遍历

二叉树中序遍历的过程

算法： InorderTraversal(v)
输入：二叉树节点v
输出： v所有后代的中序遍历序列
{
	if (null != v) {//设lc、 rc分别为v的左、右孩子
		调用InorderTraversal(lc)对v的左子树做中序遍历;
		访问并输出v;
		调用InorderTraversal(rc)对v的右子树做中序遍历;
	}
}

4.6 完全二叉树的 Java 实现

4.6.1 完全二叉树类的 Java 接口

/*
* 完全二叉树接口
*/
public interface ComplBinTree extends BinTree {
	//生成并返回一个存放e的外部节点，该节点成为新的末节点
	public BinTreePosition addLast(Object e);
	//删除末节点，并返回其中存放的内容
	public Object delLast();
	//返回按照层次遍历编号为i的节点的位置， 0 <= i < size()
	public BinTreePosition posOfNode(int i);
}

4.6.2 基于向量的实现

在完全二叉树中，
c 若节点 v 有左孩子，则 i(lchild(v)) = 2 ×i(v) + 1；
d 若节点 v 有右孩子，则 i(rchild(v)) = 2 ×i(v) + 2；
e 若节点 v 有父节点，则 i(parent(v)) = ⎣(i(v) - 1)/2⎦ = ⎡(i(v)/2⎤ - 1。
d基于可扩充向量来实现完全二叉树，则就分摊复杂度而言，每次 addLast()和
delLast()操作都可以在 O(1)时间内完成。

完全二叉树节点类的 Java 实现

/*
* 基于秩实现的完全二叉树节点
*/

public class ComplBinTreeNode_Rank extends BinTreeNode implements BinTreePosition {
	private Vector T;//所属的树
	private int rank;//在所属树中的秩
	private Object element;//存放的对象
	//构造函数
	public ComplBinTreeNode_Rank (Vector t, Object obj) {
		element = obj;
		T = t;
		rank = T.getSize();
		T.insertAtRank(rank, this);
	}
	//返回当前节点中存放的对象
	public Object getElem()
	{ return element; }
	//将对象obj存入当前节点，并返回此前的内容
	public Object setElem(Object obj)
	{ Object bak = element; element = obj; return bak; }
	//判断是否有父亲（为使代码描述简洁）
	public boolean hasParent()
	{ return (0 != rank) ? true : false; }
	//返回当前节点的父节点
	public BinTreePosition getParent()
	{ return hasParent() ? (BinTreePosition) T.getAtRank((rank-1)/2) : null; }
	//判断是否有左孩子（为使代码描述简洁）
	public boolean hasLChild()
	{ return (1+rank*2 < T.getSize()) ? true : false; }
	//返回当前节点的左孩子
	public BinTreePosition getLChild()
	{ return hasLChild() ? (BinTreePosition) (T.getAtRank(1+rank*2)) : null; }
	//判断是否有右孩子（为使代码描述简洁）
	public boolean hasRChild()
	{ return (2+rank*2 < T.getSize()) ? true : false; }
	//返回当前节点的右孩子
	public BinTreePosition getRChild()
	{ return hasRChild() ? (BinTreePosition) (T.getAtRank(2+rank*2)) : null; }
	//返回当前节点后代元素的数目
	public int getSize() {
	int size = 1;
	if (hasLChild()) size += getLChild().getSize();
	if (hasRChild()) size += getRChild().getSize();
	return size;
}
	//返回当前节点的高度
	public int getHeight() {
		int hL = hasLChild() ? getLChild().getHeight() : -1;
		int hR = hasRChild() ? getRChild().getHeight() : -1;
		return 1 + Math.max(hL, hR);
	}
	//返回当前节点的深度
	public int getDepth() {
		return hasParent() ? 1+getParent().getDepth() : 0;
	}
}

完全二叉树类的 Java 实现

/*
* 基于向量实现的完全二叉树
*/
public class ComplBinTree_Vector extends BinTree_LinkedList implements ComplBinTree {
	private Vector T;//向量
	//构造方法：默认的空树
	public ComplBinTree_Vector()
	{ T = new Vector_ExtArray(); root = null; }
	//构造方法：按照给定的节点序列，批量式建立完全二叉树
	public ComplBinTree_Vector(Sequence s)
	{ this(); if (null !=s) while (!s.isEmpty()) addLast(s.removeFirst()); }
	/*---------- BinaryTree接口中各方法的实现 ----------*/
	//返回树根（重写）
	public BinTreePosition getRoot()
	{ return T.isEmpty() ? null : posOfNode(0); }
	//判断是否树空（重写）
	public boolean isEmpty()
	{ return T.isEmpty(); }
	//返回树的规模（重写）
	public int getSize()
	{ return T.getSize(); }
	//返回树（根）的高度（重写）
	public int getHeight()
	{return isEmpty() ? -1 : getRoot().getHeight(); }
	/*---------- ComplBinTree接口中各方法的实现 ----------*/
	//生成并返回一个存放e的外部节点，该节点成为新的末节点
	public BinTreePosition addLast(Object e) {
	BinTreePosition node = new ComplBinTreeNode_Rank(T, e);
	root = (BinTreePosition) T.getAtRank(0);
	return node;
	}
	//删除末节点，并返回其中存放的内容
	public Object delLast() {
	if (isEmpty()) return null;//若树（堆）已空，无法删除
	if (1 == getSize()) root = null;//若删除最后一个节点，则树空
	return T.removeAtRank(T.getSize()-1);
	}
	//返回按照层次遍历编号为i的节点的位置， 0 <= i < size()
	public BinTreePosition posOfNode(int i) {
	return (BinTreePosition)T.getAtRank(i);
	}
}

来源于:Java数据结构,邓俊辉

posted @ 2018-09-29 23:02 XueXueLai 阅读(189) 评论(0) 编辑收藏举报

刷新页面返回顶部

CoderRyze

20200322，使用博客园的一键导入功能，从csnd导入了部分博客，但是很多csdn中的转载文章的标志与原文url连接都没有导入过来，文章仅作学习使用，侵权立删。