「题解」Luogu3599 Koishi Loves Construction
Luogu3599 Koishi Loves Construction 题解
题意简述
有两种询问：
- 对于正整数 \(n(n\leq10^5)\)，判断是否存在一种 \(1\) 到 \(n\) 的排列，使得 \(n\) 个前缀和在模 \(n\) 意义下各不相同；
- 对于正整数 \(n(n\leq10^5)\)，判断是否存在一种 \(1\) 到 \(n\) 的排列，使得 \(n\) 个前缀积在模 \(n\) 意义下各不相同；
若不存在，输出 0，否则输出 2，并给出构造。
思路
直接考虑如何何时存在及进行构造是没有头猪的，于是我们考虑先进行一个简单的暴力，尝试先找找可能的规律。
const int N = 100010;
const int INF = 0x3f3f3f3f;
template <typename T> inline void read(T &x) {
x = 0; int f = 1; char c = getchar();
for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
x *= f;
}
int T, a[N], vis[N], tmp[N];
inline bool check_sum(int x) {
memset(vis, 0, sizeof vis); tmp[0] = 0;
for (int i = 1; i <= x; ++ i) {
tmp[i] = tmp[i - 1] + a[i];
if (vis[tmp[i] % x]) return false;
vis[tmp[i] % x] = 1;
}
return true;
}
inline bool check_mul(int x) {
memset(vis, 0, sizeof vis); tmp[0] = 1;
for (int i = 1; i <= x; ++ i) {
tmp[i] = tmp[i - 1] * a[i];
if (vis[tmp[i] % x]) return false;
vis[tmp[i] % x] = 1;
}
return true;
}
inline void solve(int x) {
for (int i = 1; i <= x; ++ i) a[i] = i;
printf("NOW: %d\n", x); int flag = 0;
do {
if (check_sum(x)) {
printf(" SUM: YES\n "); flag = 1;
for (int i = 1; i <= x; ++ i) printf("%d ", a[i]); printf("\n ");
for (int i = 1; i <= x; ++ i) printf("%d ", tmp[i]); printf("\n ");
for (int i = 1; i <= x; ++ i) printf("%d ", tmp[i] % x); puts("");
}
} while (next_permutation(a + 1, a + x + 1));
if (!flag) puts(" SUM: NO"); flag = 0;
for (int i = 1; i <= x; ++ i) a[i] = i;
do {
if (check_mul(x)) {
printf(" MUL: YES\n "); flag = 1;
for (int i = 1; i <= x; ++ i) printf("%d ", a[i]); printf("\n ");
for (int i = 1; i <= x; ++ i) printf("%d ", tmp[i]); printf("\n ");
for (int i = 1; i <= x; ++ i) printf("%d ", tmp[i] % x); puts("");
}
} while (next_permutation(a + 1, a + x + 1));
if (!flag) puts(" MUL: NO");
puts("--------------------------");
}
int main() {
freopen("brute.txt", "w", stdout);
read(T); int i = 0; while (++ i <= T) solve(i); return (0 - 0);
}
Task 1
通过上面的暴力枚举，我们似乎可以找到以下可能的性质：
-
奇数除了 \(1\) 以外一定不存在合法的构造；
-
偶数一定存在合法的构造方案，为
\[a_1=n, a_2=n-1,a_{2i + 1}=2i,a_{2i+2}=n-1-2i,i\in[1,\frac n 2-1]. \]
再来看现在我们已经可以得到的结论：
- 若 \(a_i=n\)，则一定有 \(i=1\)，否则有 \(sum_i\equiv sum_{i-1}(\bmod n).\)
我们考虑对于发现的可能的性质进行证明，有
-
若 \(n\in odd\) 且 \(n\ne 1\)，那么
\[\sum_{i=1}^{n-1}i=\frac{(1+n-1)\cdot(n-1)}{2}=n\cdot\frac{n-1}{2}\equiv0(\bmod n) \]此时 \(sum_n\equiv sum_1(\bmod n)\)，不合法，于是 \(1\) 以外的奇数一定不存在合法构造。
-
显然 \(\{a_i\}\) 是一个 \(1\) 到 \(n\) 的排列，于是我们关注在模意义下的前缀和，应当有
\[sum_{2i+1}\equiv i(\bmod n),sum_{2i+2}\equiv n-1-i(\bmod n),i\in[0,\frac n 2 -1]. \]证明：
采用归纳法进行证明。当 \(i=0\) 时，显然成立。
当 \(i>1\) 时，有
\[\begin{aligned} &sum_{2i+1}=sum_{2(i-1)+2}+a_{2i+1}\equiv n-1-(i-1)+2i\equiv i(\bmod n),\\ &sum_{2i+2}=sum_{2i+1}+a_{2i+2}\equiv i+n-1-2i\equiv n-1-i(\bmod n), \end{aligned} \]于是假设成立。且显然得到的前缀和在模意义下各不相同。
综上，我们就得到了 task 1 的构造方案。
Task 2
首先来看我们已经掌握了哪些信息：
- 一定有 \(a_1=1,a_n=n\)，易证。
- 合法的序列一定不存在区间 \([\ell, r]\)，使得 \(n|\prod_{i=\ell}^ra_i\).
观察我们暴力得到的数据及样例，可以发现，似乎所有的质数都存在合法构造，非质数中 \(1\) 和 \(4\) 存在合法构造，我们尝试证明大于 \(4\) 的所有非质数不存在合法构造。
有 \(n=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}\)，如果得到的排列合法，一定满足
即
即
那么有
下图是 \(p_i=2\) 时的 \(\frac{\alpha_ip_i+1}{p_i^{\alpha_i}}\) 的图像，显然永远有 \(t<2\).
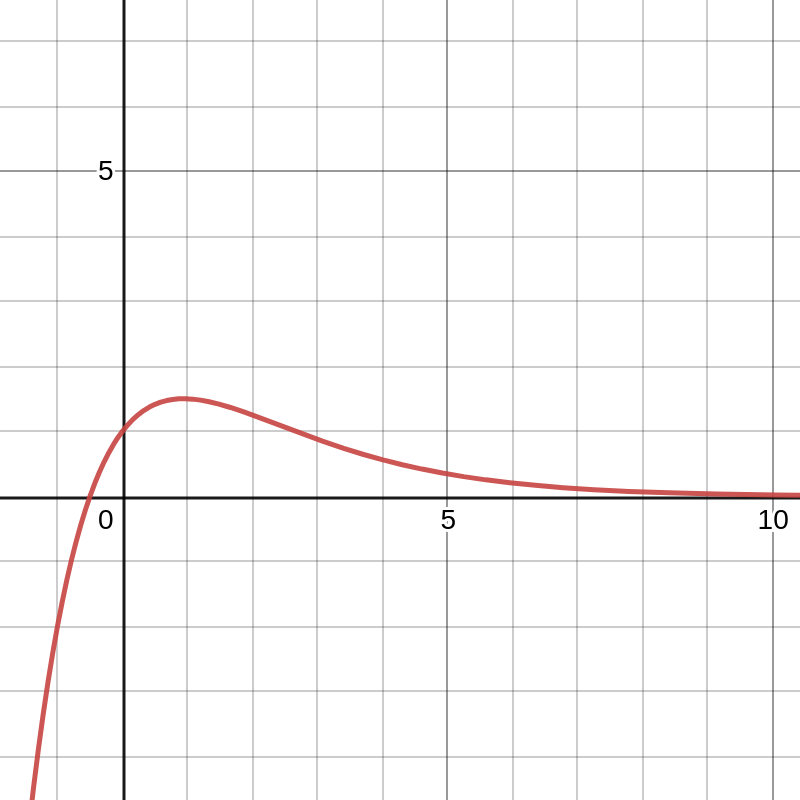
那么，当 \(p_i\) 变大时，有
显然当 \(\alpha_i\geq1\) 时，恒有 \(t<2\)，于是显然有 \(k=1\)，即 \(n\) 仅有一个质因数。
于是假设 \(n=p^{\alpha}\)，如果排列合法，应当有
当 \(\alpha\geq 2\) 时，当且仅当 \(p=2,\alpha=2\) 时上式成立。于是显然只有质数与 \(1\) 和 \(4\) 存在合法构造。
继续观察暴力所得的数据，注意到，似乎质数都存在一种构造方式，使得前缀积满足 \(mul_i\equiv i(\bmod n).\)
即满足
换句话讲，如果我们将所求数列扩展到 \(\mathbb R\)，那么构造的数列可以是 \(1,\frac 2 1,\frac 3 2,\dots,\frac n{n-1}\)，那么，如果我们将上面的实数数列依次取逆元，那么就可以得到一个整数数列，下面证明这个整数数列两两不相同。
证明：
设存在 \(a_x=a_y=k(x<y)\)，根据该数列性质，有
于是有
于是有
那么就有
显然不成立，于是假设不成立，故 \(\{a_i\}\) 两两不同。
于是我们就得到了一个可行的构造方案。
const int N = 100010;
const int INF = 0x3f3f3f3f;
template <typename T> inline void read(T &x) {
x = 0; int f = 1; char c = getchar();
for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
x *= f;
}
int x, t, n, prm[N], nprm[N], pcnt;
inline void euler(int x) {
for (int i = 2; i <= x; ++ i) {
if (!nprm[i]) prm[++ pcnt] = i;
for (int p = 1; p <= pcnt; ++ p)
if (prm[p] * i <= x) {
nprm[prm[p] * i] = true;
if (i & prm[p] == 0) break;
} else break;
}
}
inline int fpow(int x, int p) {
int res = 1;
while (p) {
if (p & 1) res = 1ll * res * x % n;
p >>= 1; x = 1ll * x * x % n;
}
return res;
}
inline void task1() {
read(n);
if (n == 1) {puts("2 1"); return;}
if (n & 1) {puts("0"); return;}
printf("2 %d %d ", n, n - 1);
for (int i = 1; i <= n / 2 - 1; ++ i)
printf("%d %d ", i << 1, n - 1 - (i << 1));
}
inline void task2() {
read(n);
if (n == 1) {puts("2 1"); return;}
if (n == 4) {puts("2 1 3 2 4"); return;}
if (nprm[n]) {puts("0"); return;}
printf("2 "); int now = 1, mul = 1;
for (int i = 1; i < n; ++ i) {
printf("%d ", now);
now = 1ll * (i + 1) * fpow(mul, n - 2) % n;
mul = 1ll * mul * now % n;
}
printf("%d\n", n);
}
int main() {
read(x), read(t);
if (x == 1) while (t --) task1();
else {euler(1e5); while (t --) task2();}
return (0 - 0);
}
总结
乍一看没有思路的构造题，考虑先暴力找到可行解，再寻找可能存在的规律，然后尝试证明。
