「数据结构」Link-Cut Tree(LCT)
LCT 的简单讲解
#1.0 简述
#1.1 动态树问题
维护一个森林，支持删除某条边，加入某条边，并保证加边、删边之后仍然是森林。我们需要维护这个森林的一些信息。
一般的操作有两点连通性，两点路径权值和等等。
#1.2 实链剖分
先来回顾一下树链剖分，我们可以按照子树大小进行剖分（重链剖分），也可以按照子树高度进行剖分（长链剖分），使得原本的一棵树被分为若干条链，然后可以在链上通过如线段树这样的数据结构维护信息。
那么，存不存在一种剖分方式能够使我们更加得心应手地处理动态树问题？显然剖出的可能会不停变换，于是我们希望我们剖出来的链能够是我们想要的，那么只要我们选择剖出我们想要的链不就行了？(～￣▽￣)～
看起来很随意是不是？但是这就是实链剖分：
- 对于一个点连向儿子的所有边，我们自己选择一条作为实边，剩下的边作为虚边。
- 实边连向的儿子是实儿子，剩下的是虚儿子。
- 一条由实边组成的链，我们称之为实链。
显然这种剖分方法是极为灵活的，灵活到一条实链上的点根本不是固定的 (lll￢ω￢)，那么驯服这种放荡不羁的树链，我们要任用一种更加灵活的数据结构进行管理——Splay（伸展树）。
关于伸展树，可以参考笔者的博客 [数据结构]伸展树(Splay)。
#1.3 辅助树
先来捋清各种名称之间的关系：
- 树上的每个节点与 Splay 上的节点一一对应 ；
- 一棵 Splay 维护一棵树上一条深度递增的链，Splay 上按照深度排序；
- 若干颗 Splay 组成一棵辅助树(AuxTree)，一棵辅助树代表一棵原树；
- 所有辅助树组成 LCT；
一个很重要的点：辅助树上的所有 Splay 并不是相互独立的。原本一棵 Splay 的根节点是不应该有父节点的，但是在辅助树上，一棵 Splay 的根节点的父节点就是这棵 Splay 维护的树链在原树上的父亲。但是，这种父亲链接的特点是：子认父而父不认子，换句话讲，这种父亲链接中的父亲所存储的左右儿子都不是这个链接中的儿子，也就是说辅助树可能并不是一棵二叉树，同时，我们也可以利用这个性质快速判断一个节点是否是所在 Splay 的根节点。
同时，Splay 可以在满足辅助树、Splay 的性质的前提下任意变换。意味着原树中的根在辅助树中不一定是根。
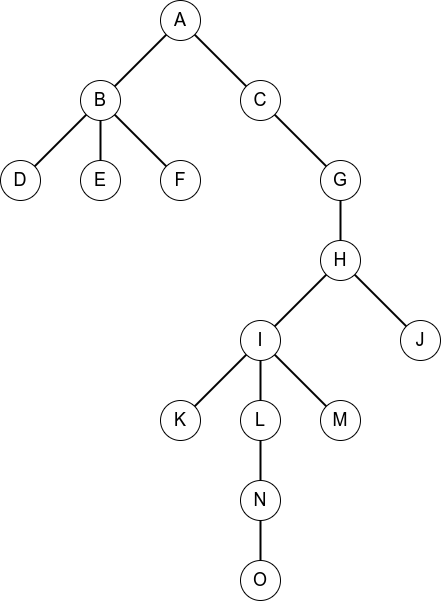
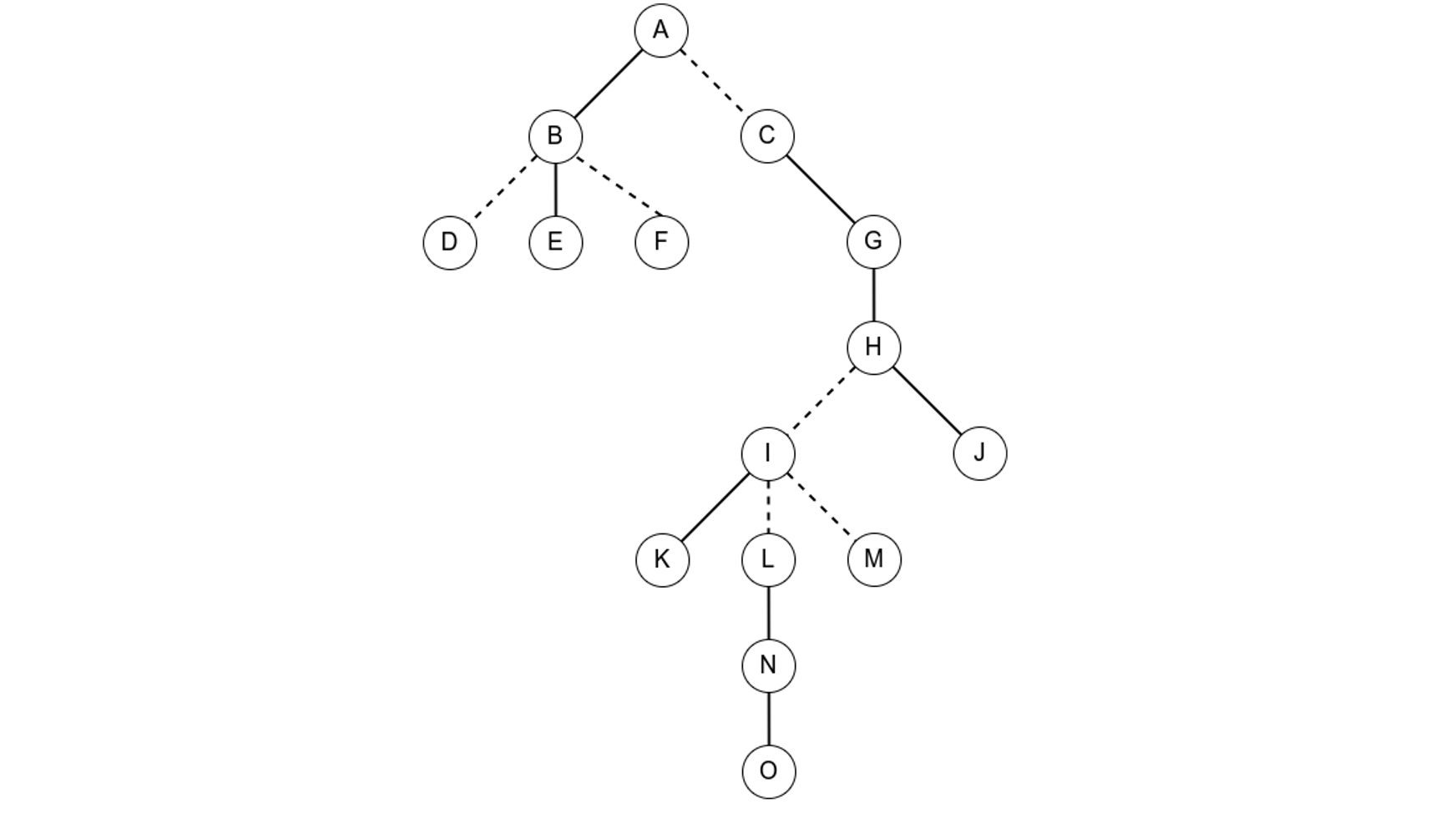
如图，这是一棵原树：
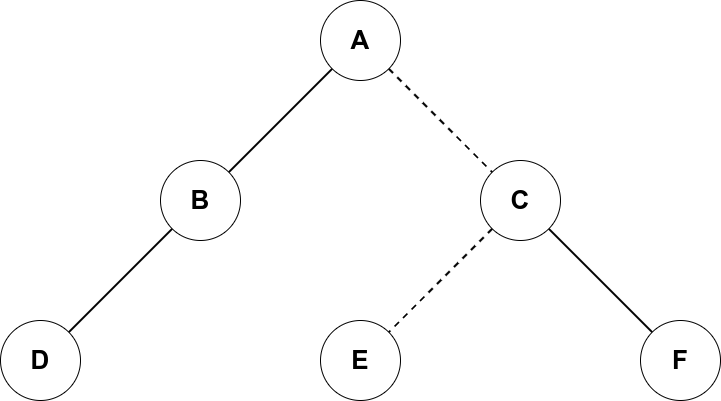
其中实线代表的是实边，虚线代表是虚边。
那么相应的辅助树可能如下（Splay 是可以变换的哦 OvO）：
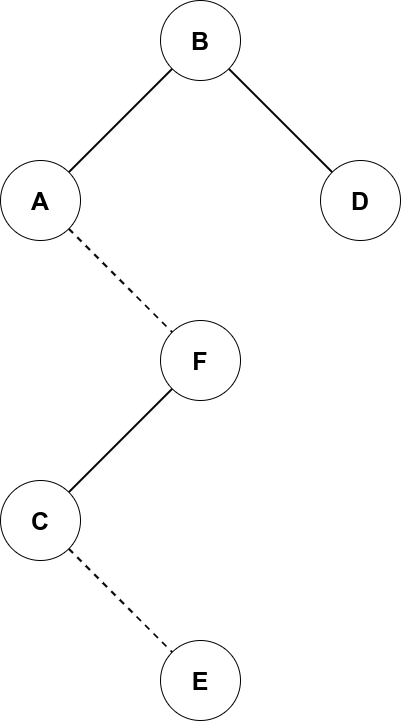
#2.0 主要函数
一些变量及其含义
直接把代码丢在这里吧 (￣▽￣)
struct Node {
int ch[2], fa; //左右儿子及父亲
int rev_tag, lzy_tag; //翻转标记及信息懒标记
int val, siz, var; //单点信息，子树大小，维护信息
} p[N];
#define f(x) p[x].fa
#define ls(x) p[x].ch[0]
#define rs(x) p[x].ch[1]
具体用途下文再说 <(ˉ^ˉ)>
一些基础操作
首先是 pushup() 和 pushdown()，没什么好说的，根据题目有所不同。
inline void pushup(int k) {
p[k].siz = p[p[k].ch[0]].siz + p[p[k].ch[1]] + 1;
/*Other things that need to be maintained.*/
}
inline void pushdown(int k) {
if (p[k].rev_tag) {
if (p[k].ch[0]) reverse(p[k].ch[0]);
if (p[k].ch[1]) reverse(p[k].ch[1]);
/*reverse() 是个什么函数请见下文*/
p[k].rev_tag = 0;
}
/*Other things that need to be maintained.*/
}
接下来是 get_type() 和 isroot()，前者获取当前节点是父亲的哪一种儿子，后者则是判断当前节点是不是所在 Splay 的根。
get_type() 是 Splay 的经典操作了，不多展开；isroot() 需要用到辅助树上 Splay 的性质：根节点的父亲不认这个儿子，所以只需要判断当前节点的父亲记录的儿子中是否包含当前节点即可。
inline int get_type(int x) {return x == p[p[x].fa].ch[1];}
inline int isroot(int x) {return x != ls(f(x)) && x != rs(f(x));}
rotate() 与 splay()
rotate() 还是将当前节点在 Splay 中上移一层，不过与经典 Splay 中的略有不同。
inline void rotate(int x) {
int y = f(x), z = f(y), op = get_type(x);
if (!isroot(y)) p[z].ch[get_type(y)] = x; //Here.
p[y].ch[op] = p[x].ch[!op], p[p[x].ch[!op]].fa = y;
p[x].ch[!op] = y, p[y].fa = x, p[x].fa = z;
pushup(y), pushup(x);
}
注意我们一定要先判断当前节点的父节点是不是根节点，然后在进行变换。至于为什么不用判断 x 是不是根节点，因为 rotate() 只会在 splay() 中被调用，然鹅 splay() 中限定了此节点不是根节点。
现在我们来看 splay()；注意到一点，我们可能需要下放许多标记，由于 Splay 本身极其灵活，我们一定要考虑将所有的标记下放之后再调整其结构，也就需要在 splay() 之前先调用一个 update() 函数进行标记的下放。
void update(int x) {if (!isroot(x)) update(f(x)); pushdown(x);}
update() 我们采用递归的形式实现，从要调整上去的节点开始，一层层向上深搜，直到到达根部，此时所有儿子可能发生变化的节点上的信息都已经下放完毕。然后我们就可以随心所欲的调教改变这棵 Splay 了。
inline void splay(int x) {
update(x);
for (int fa; fa = f(x), !isroot(x); rotate(x))
if (!isroot(fa)) rotate(get_type(fa) == get_type(x) ? fa : x);
}
这里并不会展开讲解
rotate()与splay()，因为他们都是 Splay 的基础函数，详细解释见 [数据结构]伸展树(Splay)。
Access()
首先来了解一下 Access() 的本质：将一个点 \(x\) 到原树上的根之间的路径中的所有边选择为实边，组成实链。
于是我们考虑从底部开始，一层一层向上构建。
当我们把当前处理到的点 \(x\) splay() 到所在 Splay 的根后，显然此时在他右子树中的点深度都要比 \(x\) 的深度大，一定不被包含在所要构建的 Splay 中，于是直接将其断掉；
再考虑他的父亲（在另一棵 Splay 中），我们就同样将他 splay() 到根部，考虑当前右子树中的点一定要么与 \(x\) 深度相同，要么比 \(x\) 的还要深，这些点一定都不能出现在 Splay 中，于是断掉，接上 \(x\)，那么在左子树中的点呢？他们的深度一定更浅，且根据辅助树上 Splay 的要求，这些点一定是在从 \(x\) 到根的路径上的，于是不用管。重复这个过程，直到根也被处理完。
inline int Access(int x) {
int t = 0;
for (t = 0; x; t = x, x = f(x))
splay(x), p[x].ch[1] = t, pushup(x);
return t; //这里返回的是所在 Splay 的根
}
感觉这样讲应该很清楚了吧 QwQ，但还是做了图帮助理解 <(￣ˇ￣)/
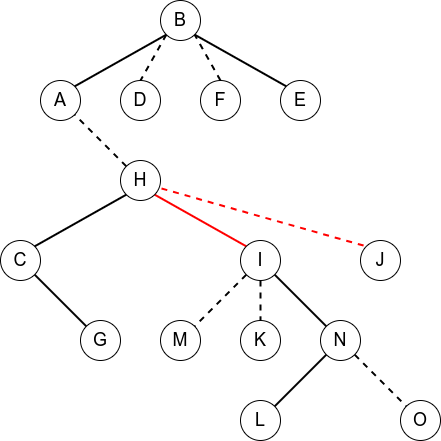
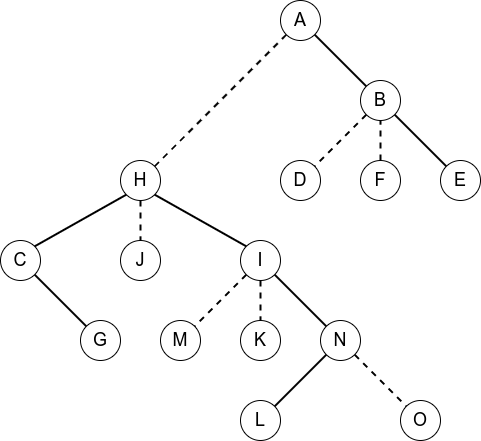
（经典老图重置版了属于是）现在我们有如下的一棵树，实线是实边，虚线是虚边。
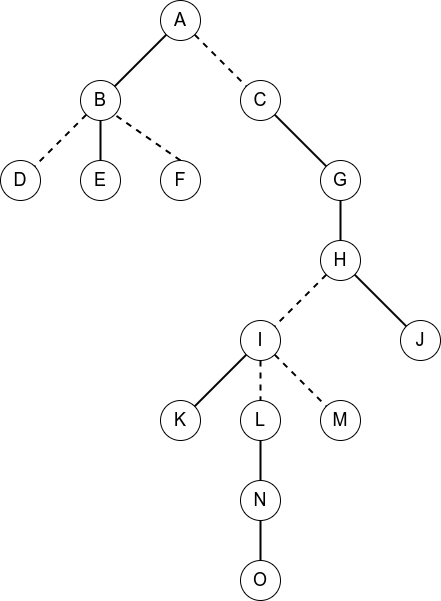
现在我们想要 Access(N)，也就是想将其变为
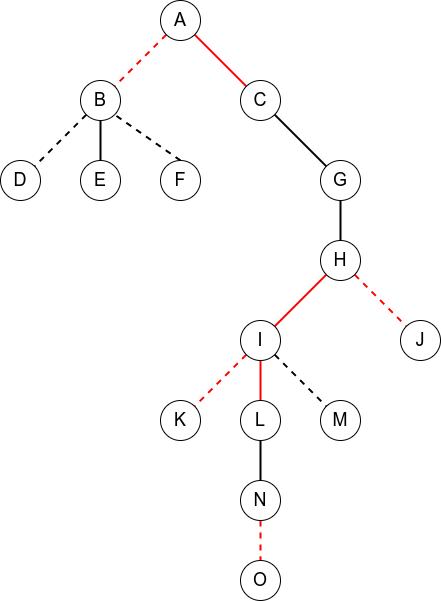
他的辅助树的一种可能的形态为
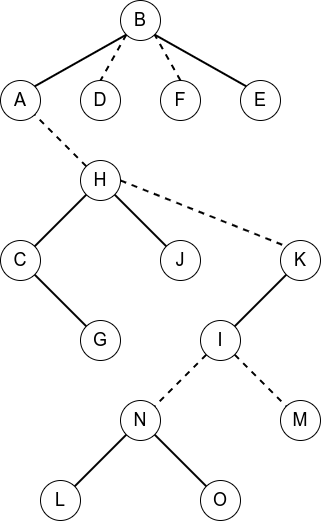
（图中实线连接的点存在于同一棵 Splay 中，红色线表示相对上一步做出了更改）
按照上面的步骤进行变换
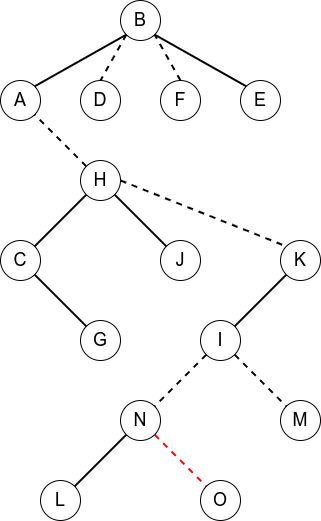
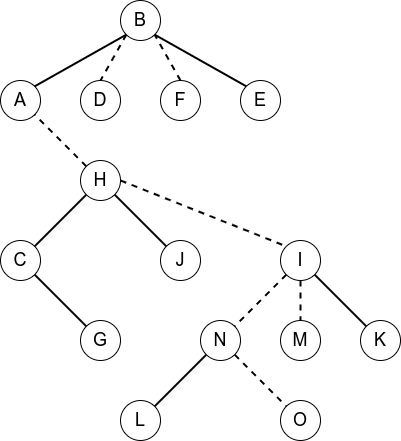
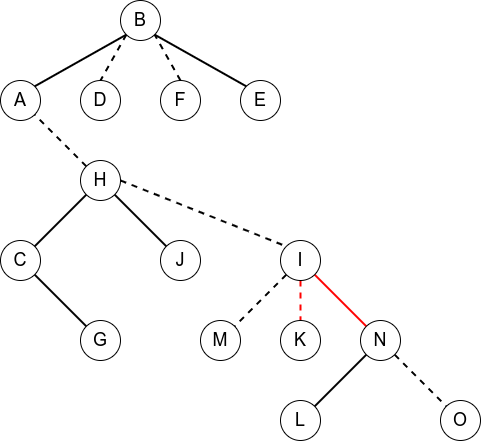
make_root() 与 find_root()
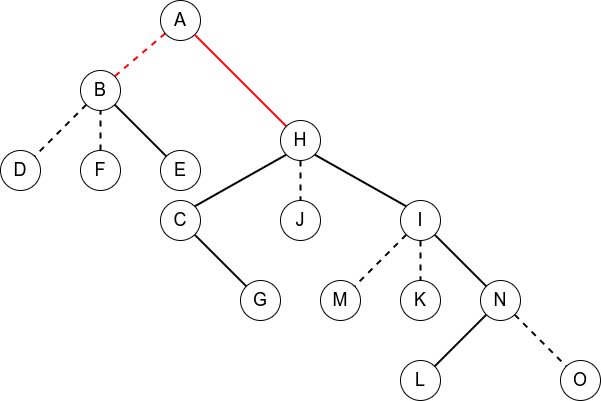
在实际运用中，我们需要维护的路径很有可能不是一条深度递增的链，但是这种链是不被允许组成一颗 Splay，由于 LCT 极为灵活，此时，如果题目性质允许，我们可以尝试将一端转换为原树的根节点。
比如这里有一棵以 \(A\) 为根的树：
现在我们要将他变为以 \(I\) 为根（红色边为父子关系变化的边）：
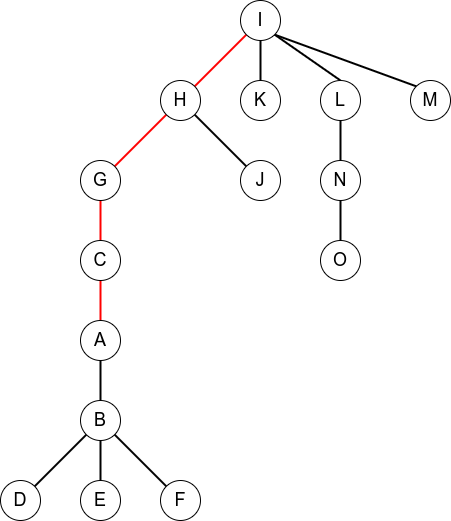
通过图片容易看出，从我们要变为根的 \(x\) 到原根的路径上的所有父子关系都应该反转，但是不在该路径上的点并没有受到影响，他的父亲该是谁还是谁。注意到，在原树上的一条链的父子关系反转就是其深度关系完全反转，于是在 Access(x) 之后，我们需要做的就是将 \(x\) 所在的 Splay 上的每个节点的左右儿子全部交换，一下做完的时间复杂度是很难被保证的，于是我们采用打标记的方式进行。
inline void reverse(int x) {swap(p[x].ch[0], p[x].ch[1]); p[x].rev_tag ^= 1;}
inline void make_root(int x) {x = Access(x); reverse(x);}
既然我们很多时候修改了原树的根，那么又该如何确定当前原树的根是谁呢？这对于我们判断两者是否在同一棵树上很重要。
同样还是利用 Splay 的性质，我们是按照深度进行的排序，于是在 Access() 之后，根一定是深度最浅的那个，于是我们直接不断进入左子树，找到最左端的节点即可。注意，我们一定要将所有的标记全部下传，少传一个标记可能整个 Splay 的结构就被粉碎了 QwQ。
inline int find_root(int x) {
x = Access(x), pushdown(x);
while (ls(x)) x = ls(x), pushdown(x);
splay(x); return x;
}
link()、cut()、split()!
叫了这么久的 Link-Cut Tree，终于讲到 link() 与 Cut() 操作了 OvO。
link() 操作很简单，显然我们只需要在确保要连接的两者不在同一棵树中，然后将一者变为所在树的根（原树与 Splay 双重意义）然后直接相连就是了。
cut() 的时候，我们同样先将其中一点 \(x\) 变为所在树的根，然后进行一波判断。
-
判断 \(y\) 与 \(x\) 是否在同一棵树中；
-
判断 \(y\) 是否是 \(x\) 的直接儿子；
- 要求 \(y\) 的父亲是 \(x\)，这是一个必要不充分条件；
- 由于父亲存的是辅助树上的父亲，\(y\) 可能是所在 Splay 的根，但是还有比他深度浅的节点（\(y\) 的左儿子），由于 Splay 维护的是从上到下的一条链，于是如果 \(y\) 有左儿子，那么一定意味着 \(x\) 和 \(y\) 之间还有其他的点。
都满足后，此时 \(y\) 一定是 \(x\) 的左儿子，于是我们就可以直接断开。
split() 实际就是单独分出原树上 \(x\to y\) 的路径，我们只需要将一者变为根，然后 Access() 另一者即可。
inline void link(int x, int y) {make_root(x); if (find_root(y) != x) splay(x), p[x].fa = y;}
inline void split(int x, int y) {make_root(x); Access(y); splay(y);}
inline void cut(int x, int y) {
make_root(x);
if (find_root(y) == x && f(y) == x && !ls(y))
p[y].fa = p[x].ch[1] = 0, pushup(x);
}
#3.0 例题
#3.1 Luogu3690 【模板】动态树（Link Cut Tree）
是真的模板呢 ( 0 - 0 )。
const int N = 300010;
const int INF = 0x3fffffff;
template <typename T> inline void read(T &x) {
x = 0; int f = 1; char c = getchar();
for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
x *= f;
}
struct Node {int val, sum, rev_tag, ch[2], fa;};
struct LCT {
#define f(x) p[x].fa
#define ls(x) p[x].ch[0]
#define rs(x) p[x].ch[1]
Node p[N];
inline LCT() {}
inline bool get_type(int x) {return x == p[f(x)].ch[1];}
inline bool isroot(int x) {return ls(f(x)) != x && rs(f(x)) != x;}
inline void pushup(int k) {p[k].sum = p[k].val ^ p[ls(k)].sum ^ p[rs(k)].sum;}
inline void reverse(int x) {swap(p[x].ch[0], p[x].ch[1]); p[x].rev_tag ^= 1;}
inline void pushdown(int x) {
if (p[x].rev_tag) {
if (ls(x)) reverse(ls(x));
if (rs(x)) reverse(rs(x));
p[x].rev_tag = 0;
}
}
void update(int x) {if (!isroot(x)) update(f(x)); pushdown(x);}
inline void rotate(int x) {
int y = f(x), z = f(y), op = get_type(x);
if (!isroot(y)) p[z].ch[get_type(y)] = x;
p[y].ch[op] = p[x].ch[!op], p[p[x].ch[!op]].fa = y;
p[x].ch[!op] = y, p[y].fa = x, p[x].fa = z;
pushup(y), pushup(x);
}
inline void splay(int x) {
update(x);
for (int fa; fa = f(x), !isroot(x); rotate(x))
if (!isroot(fa)) rotate(get_type(fa) == get_type(x) ? fa : x);
}
inline int Access(int x) {
int t = 0;
for (t = 0; x; t = x, x = f(x))
splay(x), p[x].ch[1] = t, pushup(x);
return t;
}
inline int find_root(int x) {
x = Access(x), pushdown(x);
while (ls(x)) x = ls(x), pushdown(x);
splay(x); return x;
}
inline void make_root(int x) {x = Access(x); reverse(x);}
inline void link(int x, int y) {make_root(x); if (find_root(y) != x) splay(x), p[x].fa = y;}
inline void split(int x, int y) {make_root(x); Access(y); splay(y);}
inline void cut(int x, int y) {
make_root(x);
if (find_root(y) == x && f(y) == x && !ls(y))
p[y].fa = p[x].ch[1] = 0, pushup(x);
}
} lct;
int n, m;
int main() {
read(n), read(m);
for (int i = 1; i <= n; ++ i) read(lct.p[i].val);
while (m --) {
int op = 0, x = 0, y = 0;
read(op), read(x), read(y);
if (op == 0) lct.split(x, y), printf("%d\n", lct.p[y].sum);
else if (op == 1) lct.link(x, y);
else if (op == 2) lct.cut(x, y);
else lct.splay(x), lct.p[x].val = y;
}
return 0;
}
#3.2 「HNOI2010」弹飞绵羊
我们将 \(i+k_i\) 作为 \(i\) 的父亲节点，显然每个点最多只有一个出边，并且至少有一个点没有出边，显然这会构成一个森林，每次修改弹簧劲度时，实际就是断边然后重连，于是显然可以 LCT.
注意到，我们每次询问时要查询的东西就是从 \(x\) 到所在树的根构成的链上一共有多少个节点，于是我们的树根是不方便改变的，于是就没有办法使用 make_root()，对于 link() 的影响不大，因为连接时一定是刚断开这个位置的边，如果我们不能改变原树的根，那么此时这个点一定是所在树的根，于是只需要把他拉到所在 Splay 的根部即可。同时，由于 cut() 的操作完全由我们操作，任一时刻一定是合法的，于是便不需要使用 make_root() 来辅助判断合法性。假如我们要断开 \(x\) 和 \(y\) 之间的边，我们只需要先 Access(x)，由于 \(y\) 是 \(x\) 的父亲，于是这样 \(y\) 与 \(x\) 一定在同一棵 Splay 上，然后 splay(y)，由于在原树中 \(y\) 是 \(x\) 的直接父亲，此时 \(x\) 一定是 \(y\) 的右儿子，直接断开即可。
查询时直接 Access() 然后返回所在 Splay 上的节点数即可。
剩下的都是 LCT 的板子了，这道题我们充分运用了 LCT 的灵活性。
const int N = 200010;
const int INF = 0x3fffffff;
template <typename T> inline void read(T &x) {
x = 0; int f = 1; char c = getchar();
for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
x *= f;
}
struct Node {int siz, ch[2], fa;};
struct LCT {
#define ls(x) p[x].ch[0]
#define rs(x) p[x].ch[1]
#define f(x) p[x].fa
Node p[N]; int siz;
inline LCT() {siz = 0;}
inline void init(int _siz) {siz = _siz; for (int i = 1; i <= siz; ++ i) p[i].siz = 1;}
inline void pushup(int k) {p[k].siz = p[ls(k)].siz + p[rs(k)].siz + 1;}
inline int get_type(int k) {return rs(f(k)) == k;}
inline bool isroot(int k) {return ls(f(k)) != k && rs(f(k)) != k;}
inline void rotate(int x) {
int y = f(x), z = f(y), op = get_type(x);
if (!isroot(y)) p[z].ch[get_type(y)] = x;
p[y].ch[op] = p[x].ch[!op], p[p[x].ch[!op]].fa = y;
p[x].ch[!op] = y, p[y].fa = x, p[x].fa = z;
pushup(y), pushup(x);
}
inline void splay(int x) {
for (int fa; fa = f(x), !isroot(x); rotate(x))
if (!isroot(fa)) rotate(get_type(fa) == get_type(x) ? fa : x);
}
inline int Access(int x) {
int t = 0;
for (t = 0; x; t = x, x = f(x))
splay(x), p[x].ch[1] = t, pushup(x);
return t;
}
inline void link(int x, int y) {splay(x), p[x].fa = y;}
inline void cut(int x, int y) {
Access(x); splay(y); p[y].ch[1] = p[x].fa = 0; pushup(y);
}
inline int query(int x) {Access(x); splay(x); return p[x].siz;}
} lct;
int n, m, to[N];
inline void modify(int x, int y) {
if (x + to[x] <= n) lct.cut(x, x + to[x]);
if (x + y <= n) lct.link(x, x + (to[x] = y));
}
int main() {
read(n); lct.init(n);
for (int i = 1; i <= n; ++ i) read(to[i]);
for (int i = 1; i <= n; ++ i)
if (i + to[i] <= n) lct.link(i, i + to[i]);
read(m);
while (m --) {
int op = 0, x = 0, y = 0; read(op), read(x); ++ x;
if (op == 1) printf("%d\n", lct.query(x));
else read(y), modify(x, y);
}
return 0;
}
#4.0 时间复杂度分析
对于 LCT 的时间复杂度分析我们采用势能法，详情见笔者博客势能分析法 - #2.4 LCT 的时间复杂度分析.
