关于我想了很久才想出这题咋做这档事 - 1
#0.0 目录
目录中以下题目皆可点击查看原题
#1.0 P2004 领地选择
不难想到,这里就是让在一个有 \(N \times M\) 个点的矩形中,找到有 \(C \times C\) 个点的正方形,使各点之和最大,那么很自然的就会想到二维前缀和
我们在读入点 \((i,j)\)时,第 \(i-1\) 行的数以及点 \((i,j)\) 左边的数都已被读入,所以我们可以在一个点输入时便算出他的前缀和,那么他的前缀和怎么算?如图:

这张图就知道了 \((i,j)\) 可以由 \((i-1,j)\)和 \((i,j-1)\) 两块构成,不过要注意两个点
- 有一块矩阵我们重复加了,也就是 \((i-1,j-1)\) 这一块,所以我们要减去它
- 我们这个矩阵是不完整的,由图可知我们还有一块深蓝色的没有加,也就是 \((i,j)\) 这一点,所以我们要再加上该点的值
该点前缀和即为DP[i][j]=DP[i-1][j]+DP[i][j-1]-DP[i-1][j-1]+map[i][j]
如下图,我们可以凭借前缀和算出以 \((i,j)\) 为正方形右下角时,所能得到的各点之和

为 S=DP[i][j]-DP[i-c][j]-DP[i][j-c]+dp[j-c][i-c],这里原理与上面相同,不过是将 \(1\) 变成了 \(c\)
之后比较所得答案大小,对现有答案进行更新,时间复杂度为 \(O(n \cdot m)\)
#include <iostream>
#include <cstdio>
#define SIZE 10010
using namespace std;
int n,m,c;
int ma[SIZE][SIZE],ans[3];
int main(){
ans[0] = -0x3fffffff;
scanf("%d%d%d",&n,&m,&c);
for (int i = 1;i <= n;++ i)
for (int j = 1;j <= m;++ j){
scanf("%d",&ma[i][j]);
ma[i][j] = ma[i - 1][j] + ma[i][j - 1] - ma[i - 1][j - 1] + ma[i][j];
if (i >= c && j >= c){
int s = ma[i][j] - ma[i - c][j] - ma[i][j - c] + ma[i - c][j - c];
if (ans[0] < s){
ans[0] = s;
ans[1] = i - c + 1;
ans[2] = j - c + 1;
}
}
}
printf("%d %d",ans[1],ans[2]);
return 0;
}
#2.0 P3916 图的遍历
最初的想法是dfs加记忆化,但遗憾并没有实现,在计算时会遇到错误,所以换一个思路。
我们要找从点 \(v\) 出发能到达的编号最大的点,显然,这个最大编号的点到点 \(v\) 之间显然是有路可走的,正着来不行,那么我们可否可以从反方向建图,从编号大的点 \(u\) 开始dfs,能遍历到的点所能达到的最大的点显然就是这个点 \(u\),对每个点进行标记,后面再次遍历时便不会再进行更新(显然后面的遍历起始点 \(i\) 的编号小于当前点 \(u\) 的编号),由于每个点只遍历 \(1\) 次,故时间复杂度为 \(O(n)\)
#include <iostream>
#include <cstdio>
#include <cstring>
#define SIZE 100011
using namespace std;
struct Edge{
int to;
int next;
};
Edge e[SIZE];
int n,m,tot;
int head[SIZE],vis[SIZE],ans,sum[SIZE];
inline void add(int v,int u){
e[tot].to = v;
e[tot].next = head[u];
head[u] = tot;
tot ++;
}
inline void dfs(int p,int st){
if (sum[p])
return;
sum[p] = st;
for (int j = head[p];j != -1;j = e[j].next){
if (!sum[e[j].to])
dfs(e[j].to,st);
}
}
int main(){
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&m);
for (int i = 0;i < m;i ++){
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
}
for (int i = n;i > 0;i --)
dfs(i,i);
for (int i = 1;i <= n;i ++)
printf("%d ",sum[i]);
return 0;
}
#3.0 P4017 最大食物链计数
看题面描述,不难想到以下几点:
- 这是个有向无环图(DAG)
- 我们要从入度为零的点开始查找
- 每次要等一个点的入度为零后才可以将它入队,
- 我们要求从所有入度为零的点到出度为零的点总路径数
显然,我们要用 拓扑排序 来做
假设有以下一个图:
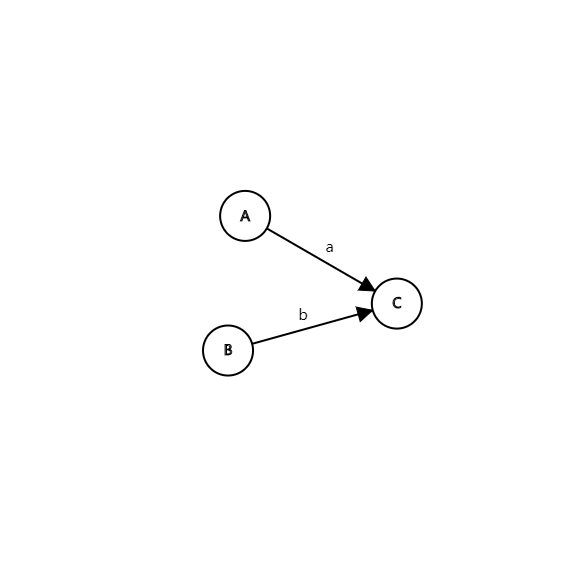
由入度为零的点到点A有 \(a\) 条路径
由入度为零的点到点B有 \(b\) 条路径
根据加法原理,由入度为零的点到点C有 \(a+b\) 条路径
思路并不难,将入度为零的点入队,
之后对队头的点 \(i\) 进行遍历,同时将点 \(i\) 可达到的点 \(j\) 的入度减一,点 \(j\) 的答案数加上点 \(i\) 的答案数;如果点 \(j\) 的入度为零,将该点入队
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define SIZE 500010
#define Mod 80112002
using namespace std;
struct Edge{
int from;
int to;
int next;
};
Edge e[SIZE];
int n,m,ans,tot;
int head[SIZE],out[SIZE],in[SIZE],sum[SIZE];
queue <int> q;
inline void add(int u,int v){
e[tot].to = v;
e[tot].next = head[u];
head[u] = tot;
in[v] ++;
out[u] ++;
tot ++;
}
int main(){
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&m);
for (int i = 1;i <= m;i ++){
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
}
for (int i = 1;i <= n;i ++)
if (in[i] == 0){
sum[i] = 1;
q.push(i);
}
while (!q.empty()){
int now = q.front();
q.pop();
for (int i = head[now];i != -1;i = e[i].next){
sum[e[i].to] += sum[now];
sum[e[i].to] %= Mod;
in[e[i].to] --;
if (!in[e[i].to])
if (!out[e[i].to]){
ans += sum[e[i].to];
ans %= Mod;
}
else
q.push(e[i].to);
}
}
printf("%d",ans);
return 0;
}
#4.0 P1038 神经网络
首先,根据题面,我们可以知道以下几点:
- 每个图都是一个有向无环图(DAG)
- 点 \(C_i\) 的计算公式为 \(C_i=\sum\limits_{(j,i)\in E}W_{ji}C_j-U_i\),其中 \((j,i)\in E\) 为所有以 \(i\) 为终点的边,\(W_{ji}\) 为这条边的权值,\(U_i\) 为阈值
- 要从入度为 \(0\) 的点开始向后计算,点 \(i\) 的 \(C_i\) 要算出后才可以向后传递(注意只有当 \(C_i>0\) 时才会后传)
- 我们要求每个出度为 \(0\) 的点的 \(C\) 值
关于第2点的公式,我们可以这么理解,每遍历到一条以 \(i\) 为终点的边,对 \(C_i\) 进行一次更新,然后使点 \(i\) 的入度减一,当点 \(i\) 的入度为 \(0\) 后,便可以用它向下传递信息,这样也同时满足了第三点
综上,我们很容易想到用 拓扑排序 来做这道题
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
#define SIZE 100010
using namespace std;
struct Node{ //每个点拥有的数值
int c;
int thre;
int in;
int out;
};
Node d[SIZE];
struct Edge{ //每条边拥有的数值
int u;
int v;
int w;
int next;
};
Edge e[SIZE];
queue <int> q;
int n,p,head[SIZE],tot,f;
inline void add(int u,int v,int w){ //加边,记得对点的入度和出度进行更新
e[tot].u = u;
e[tot].v = v;
e[tot].w = w;
e[tot].next = head[u];
head[u] = tot;
tot ++;
d[u].out ++;
d[v].in ++;
}
int main(){
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&p);
for (int i = 1;i <= n;i ++){
scanf("%d%d",&d[i].c,&d[i].thre);
if (d[i].c > 0)//只有输入层的点一开始就有状态,即为入度为0的点
q.push(i);
else
d[i].c -= d[i].thre; //阈值是迟早要减掉的,但输入层也有可能有阈值但不用减掉
}
for (int j = 1;j <= p;j ++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
}
while (!q.empty()){
int now = q.front();
q.pop();
if (d[now].c <= 0) //只有C大于0才会后传信息
continue;
for (int i = head[now];i != -1;i = e[i].next){ //边的遍历
d[e[i].v].c += e[i].w * d[now].c; //更新终点的C值与入度
d[e[i].v].in --;
if (!d[e[i].v].in) //当该点入度为0时开始后传信息
q.push(e[i].v);
}
}
for (int i = 1;i <= n;i ++) //注意输出格式
if (!d[i].out && d[i].c > 0){
f = 1;
printf("%d %d\n",i,d[i].c);
}
if (!f)
printf("NULL");
return 0;
}
更新日志及说明
更新
- 初次完成编辑 - \(2020.10.17\)
- 增添了 #4.0 P1038 神经网络 的内容
本文若有更改或补充会持续更新


