[五年CSP三年模拟]CSP2020-J冲刺 - 初赛篇

#0.0 前言

每次的CSP考试前最担心的就是初赛，翻看了许多资料，还是觉得自己整理最有助于自己的理解，因而作此篇，望有助

#1.0 网络常识

#1.1 网络的分类

按地域范围

  • 局域网 范围在一般在\(1km\)的范围内，缩写为\(LAN\)(Loacl Area Network)
  • 城域网 范围在几千米到几十千米以内，缩写为\(MAN\)(Metorpolitan Area Network)
  • 广域网 范围在几十千米到几千千米以上，缩写为\(WAN\)(Wide Area Network)

注意：\(MAN\)和\(WAN\)一般都是由多个\(LAN\)构成的

按拓扑结构

  • 星型 单个站点故障不会影响全网，依赖中央节点，连线费用大
  • 总线型 总线本身的故障对系统是毁灭性的
  • 环形 站点的故障会引起整个网络的崩溃
  • 网状型（不规则形） 一般广域网属于不规则形，\(Internet\)网是当今世界规模最大、用户最多、影响最广泛的计算机互联网络

#1.2 网络的体系结构

开放式系统互联模型（英语：Open System Interconnection Model，缩写：OSI；简称为OSI模型）是一种概念模型，由国际标准化组织(ISO)提出，一个试图使各种计算机在世界范围内互连为网络的标准框架。

TCP/IP（Transmission Control Protocol/Internet Protocol，传输控制协议/网际协议）是指能够在多个不同网络间实现信息传输的协议簇。TCP/IP协议不仅仅指的是TCP 和IP两个协议，而是指一个由FTP、SMTP、TCP、UDP、IP等协议构成的协议簇， 只是因为在TCP/IP协议中TCP协议和IP协议最具代表性，所以被称为TCP/IP协议。

OSI模型与TCP/IT模型的对应关系

例题

NOIP 2012 普及组初赛试题第十题（限于篇幅，这里不展示原题）

#1.3 IP地址

IP地址是IP协议提供的一种统一的地址格式，它为互联网上的每一个网络和每一台主机分配一个逻辑地址，以此来屏蔽物理地址的差异。
该地址通常用由句点分隔的八位字节的十进制数表示，即4段二进制位组成，每组数字取值范围只能是\(0 \sim 255\)，如：
10000001 00001011 00000011 00011111
IP地址即为：129.11.3.31
IP地址分为A、B、C、D、E五类，如下图

注意：主机ID所有域不能都为0或255，如网络ID为10，那么就不能把10.0.0.0和10.255.255.255两个IP地址分给任何主机；如网络ID为192.114.31，那么就不能把192.114.31.0和192.114.31.255两个IP地址分给任何主机

#2.0 数制转换

为表达方便，常在数字后加一缩写字母后缀作为不同进制数的标识
各进制的后缀字母：

  • B:二进制数
  • O:八进制数
  • D:十进制
  • H:十六进制

#2.1 十进制与二进制的互相转换

二进制转十进制

  • 按权展开求和

如，

\[\begin{align*} (1011.01)_2 & =(1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 + 0 \times 2^{-1} + 1 \times 2^{-2})_{10}\\ & = (8 + 0 + 2 + 1 + 0 + 0.25)_{10} = (11.25)_{10} \end{align*}\]

十进制整数转二进制

  • 除以2取余，逆序输出

    所以\((5)_{10}=(101)_2\)

十进制小数转二进制

  • 乘以2取余，顺序输出

    所以\((0.625)_{10}=(0.101)_2\)

#2.2 八进制与二进制的互相转换

八进制转二进制

将每位八进制数转化为3位二进制数，如\((37.416)_8\)

所以\((37.416)_8=(11111.10000111)_2\)

二进制转八进制

将二进制数3位一组转化为八进制数，整数部分位数不够在前面加'\(0\)'，小数部分位数不够在后面加'\(0\)'，如\((11111.10000111)_2\)

所以\((11111.10000111)_2=(37.416)_8\)

#2.3 十六进制与二进制的互相转换

十六进制转二进制

将每位十六进制数转化为4位二进制数，如\((5DF.9)_{16}\)

所以\((5DF.9)_{16}=(10111011111.1001)_2\)

二进制转十六进制

将二进制数4位一组转化为十六进制数，整数部分位数不够在前面加'\(0\)'，小数部分位数不够在后面加'\(0\)'，如\((10111011111.1001)_2\)

所以\((10111011111.1001)_2=(5DF.9)_{16}\)

#2.4 十进制与八进制、十六进制的转换

八进制转十进制：\((\overline{a_0a_1a_2a_3...a_n})_8=(a_0 \cdot 8^n + a_1 \cdot 8^{n-1} + a_2 \cdot 8^{n-2} +...+ a_n \cdot 8^0)_{10}\)
如：\((36)_8=(3 \times 8^1 + 6 \times 8^0)_{10} = (24 + 6)_{10} = (30)_{10}\)
十六进制转十进制：\((\overline{a_0a_1a_2a_3...a_n})_{16}=(a_0 \cdot 16^n + a_1 \cdot 16^{n-1} + a_2 \cdot 16^{n-2} +...+ a_n \cdot 16^0)_{10}\)
如：\((1E)_{16}=(1 \times 16^1 + 14 \times 16^0)_{10} = (16 + 14)_{10} = (30)_{10}\)
(其实与二进制转十进制是一样的)

十进制转八进制和十六进制：与二进制一样可使用短除法

#2.5 拓展 - 关于以上进制转换的の思考

Q:为什么二进制按权展开求和得到的是对应的十进制？

设 \(b\) 是大于 \(1\) 正整数，则每个正整数 \(n\) 可唯一的表示成

\[\begin{align} n & =a_{k-1}b^{k-1}+a_{k-2}b^{k-2}+ \cdots +a_{1}b+a_{0}\\ \end{align}\]

其中 \(a_i\) 是整数， \(0 \leqslant a_{i} \leqslant b-1,i=1, \cdots ,k-1\)，且首项系数 \(a_{k-1} \ne 0\)

证明：
运用欧几里得除法，以得到所期望的表达式
首先，用 \(b\) 去除 \(n\) 得到

\[\begin{gather*} n=q_0b+a_0, \ 0 \leqslant a_{0} \leqslant b-1 \end{gather*}\]

再用 \(b\) 去除不完全商 \(q_0\) 得到

\[\begin{gather*} q_0=q_1b+a_1, \ 0 \leqslant a_{1} \leqslant b-1 \end{gather*}\]

继续进行这种运算，依次得到

\[\begin{gather*} q_{1}=q_{2}b+a_{2}, \ 0 \leqslant a_{2} \leqslant b-1\\ q_{2}=q_{3}b+a_{3}, \ 0 \leqslant a_{3} \leqslant b-1\\ \vdots\\ q_{k-3}=q_{k-2}b+a_{k-2}, \ 0 \leqslant a_{k-2} \leqslant b-1\\ q_{k-2}=q_{k-1}b+a_{k-1}, \ 0 \leqslant a_{k-1} \leqslant b-1\\ \end{gather*}\]

因为

\[\begin{gather*} 0 \leqslant q_{k-1}<q_{k-2}< \cdots <q2<q1<q0<n\\ \end{gather*}\]

所以必有整数 \(k\) 使得不完全商 \(q_{k-1}=0\)
这样，依次得到

\[\begin{aligned} n & =q_{0}b+a_{0}\\ n & =(q_{1}b+a_{1})b+a_{0}=q_{1}b^{2}+a_{1}b+a_{0}\\ \qquad & \vdots\\ n & =q_{k-3}b^{k-2}+a_{k-3}b_{k-3}+ \cdots +a_{1}b+a_{0}\\ n & =q_{k-2}b^{k-1}+a_{k-2}b_{k-2}+ \cdots +a_{1}b+a_{0}\\ & =(q_{k-1}b+a_{k-1})b^{k-1}+a_{k-2}b_{k-2}+ \cdots +a_{1}b+a_{0}\\ & =a_{k-1}b^{k-1}+a_{k-2}b_{k-2}+ \cdots +a_{1}b+a_{0}\\ \end{aligned}\]

我们还需要证明这个表达式 \((1)\) 是唯一的，假设有两种不同的表达式：

\[\begin{gather*} n=a_{k-1}b^{k-1}+a_{k-2}b^{k-2}+ \cdots +a_{1}b+a_{0}, \qquad 0 \leqslant a_{i} \leqslant b-1,i=1, \cdots ,k-1.\\ n=c_{k-1}b^{k-1}+c_{k-2}b^{k-2}+ \cdots +c_{1}b+c_{0}, \qquad 0 \leqslant c_{i} \leqslant b-1,i=1, \cdots ,k-1.\\ \end{gather*}\]

两式相减得

\[\begin{gather*} (a_{k-1}-c_{k-1})b^{k-1}+(a_{k-2}-c_{k-2})b^{k-2}+ \cdots +(a_{1}-c_{1})b+(a_{0}-c_{0})=0\\ \end{gather*}\]

假设 \(j\) 是最小的正整数使得 \(a_{j} \ne b_{j}\)，则

\[\begin{gather*} ((a_{k-1}-c_{k-1})b^{k-1-j}+(a_{k-2}-c_{k-2})b^{k-2-j}+ \cdots +(a_{j+1}-c_{j+1})b+(a_{j}-c_{j}))b^{j}=0\\ \end{gather*}\]

或者

\[\begin{gather*} (a_{k-1}-c_{k-1})b^{k-1-j}+(a_{k-2}-c_{k-2})b^{k-2-j}+ \cdots +(a_{j+1}-c_{j+1})b+(a_{j}-c_{j})=0\\ \end{gather*}\]

因此

\[\begin{align*} a_{j}-c_{j} & =-((a_{k-1}-c_{k-1})b^{k-1-j}+(a_{k-2}-c_{k-2})b^{k-2-j}+ \cdots +(a_{j+1}-c_{j+1})b)\\ a_{j}-c_{j} & =-((a_{k-1}-c_{k-1})b^{k-2-j}+(a_{k-2}-c_{k-2})b^{k-3-j}+ \cdots +(a_{j+1}-c_{j+1}))b\\ \end{align*}\]

故

\[\begin{gather*} b|(a_{j}-c_{j}),\qquad |a_{j}-c_{j}| \geqslant b\\ \end{gather*}\]

但

\[\begin{gather*} 0 \leqslant a_{j} \leqslant b-1,0 \leqslant c_{j} \leqslant b-1\\ \end{gather*}\]

又有 \(|a_{j}-c_{j}| < b\)，冲突，也就是说 \(n\) 的表达式是唯一的

证毕.

由上面的证明我们可以得到，每个十进制正整数 \(n\) 可唯一的表示成

\[\begin{align*} n & =a_{k-1}b^{k-1}+a_{k-2}b^{k-2}+ \cdots +a_{1}b+a_{0},\qquad b>1,a_{k-1} \ne 0\\ \end{align*}\]

我们又知道任何进制中，每个数都可以按位权展开成各个数位上的数字乘以对应数位的位权再相加的形式，
以十进制为例，如：
\((3452)_{10} = (3 \times 10^3 + 4 \times 10^2 + 5 \times 10^1 + 2 \times 10^0)_{10}\)
那么，这里每一位所乘的数，为什么是 \(1000,100,10,1\) 而不是 \(8,4,2,1\) ？
很简单，因为这是十进制，每一位满十向下一位进一

看整数部分，第一位向第二位进一需要十，所以第二位上每一个 "\(1\)" 就有10，同理，第二位到第三位也需要十，就是 \(10 \times 10 = 10^2\)，第三位到第四位也需要十，就是 \(10 \times 10 \times 10= 10^3\) ......

我们丢开十进制，看二进制：
二进制与十进制相似，只不过是满二进一，所以很简单可以得到，第一位向第二位进一需要二，所以第二位上每一个 "\(1\)" 就有2，同理，第二位到第三位也需要二，就是 \(2 \times 2 = 2^2\)，第三位到第四位也需要二，就是 \(2 \times 2 \times 2= 2^3\) ......

而其他进制与此相同

所以可表示成 \((\overline{a_{k-1}a_{k-2}a_{k-3}a_{k-4} \cdots a_{0}})_b=(a_{k-1} \cdot b^{k-1} + a_{k-2} \cdot b^{k-2} + a_{k-3} \cdot b^{k-3} + \cdots + a_1 + a_0 \cdot b^0)_{10}\)

对应着一个唯一的十进制正整数 \(n\)

#2.6 例题

NOIP 2018 普及组初赛试题第二题

下列四个不同进制的数中，与其它三项数值上不相等的是
 A. (269)16
 B. (617)10
 C. (1151)8
 D. (1001101011)2
(269)16=(617)10
(617)10=(617)10
(1151)8=(617)10
(1001101011)2=(619)10
故选 D

#3.0 信息编码

#3.1 储存容量

比特(bit) 是指1位二进制的数码（即0或1）。比特是计算机中表示信息的数据编码中的最小单位
字节(Byte) 通常用8个二进制数字表示一个字节，即一个字节由8个比特组成，字节是储存器系统最小的存取单位

储存容量单位间换算

\(1KB=1024B\)
\(1MB=1024KB\)
\(1GB=1024MB\)
\(1TB=1024GB\)

例题

NOIP 2018 普及组初赛试题第三题

1MB 等于（ ）
 A. 1000 字节
 B. 1024 字节
 C. 1000 * 1000 字节
 D. 1024 * 1024 字节
1MB=1024KB 1KB=1024B
所以 1MB=1024 * 1024 B
选 D

CSP 2019 入门组第一轮第三题

一个32位整型变量占用（）个字节。
 A. 32
 B. 128
 C. 4
 D. 8
一个字节有8位，即32/8=4个字节
选 C

#3.2 ASCII码

记住 '\(a\)'为 \(97\) ，'\(A\)'为 \(65\) ，'\(0\)'为 \(48\)即可，其他都可以计算得到

#3.3 汉字信息编码

汉字交换码

由使用频度分为一级汉字和二级汉字

字形储存码

一般用点阵储存，在相同点阵中，不管其笔画繁简，所占字节数相同

#4.0 原码·反码·补码

#4.1 原码

原码表示法是一种简单的机器数表示法，即符号和数值表示法。
用二进制表示，最左边的一位为符号位，剩下为数值位
符号位 '\(1\)' 表示负数，'\(0\)' 表示正数

  • 正数的原码就是他本身
  • 负数的原码符号位为 '\(1\)'
  • \(0\) 有两种表示方法，为 '\(+0(000...0)\)' 和 '\(-0(100...0)\)'

设 \(x\) 为真值，则 \([x]_原\) 为原码
如，设 \(x=1100110\)，则 \([x]_原=01100110\)
设 \(x=-1100110\)，则 \([x]_原=11100110\)

原码可表示的范围（\(n\) 位二进制）： \(0 \sim 2^n - 1\)（无符号），\(-(2^{n-1}-1) \sim 2^{n-1}-1\)（有符号）
如8位二进制，无符号表示范围为 \(0 \sim 255\)，有符号表示范围为 \(-127 \sim 127\)

原码不能直接参加运算，可能会出错，如 \(1+(-1)=0\)，而 \(00000001+10000001=10000010\)，答案为 \(-2\)，显然错误

#4.2 反码

反码通常是用来由原码求补码或者由补码求原码的过渡码

  • 当原码为正数时，反码与原码一致
  • 当原码为负数时，反码是原码除符号位外，其他位按位取反。
  • \(0\) 有两种表示方法，为 '\(+0(000...0)\)' 和 '\(-0(111...1)\)'

设 \(x\) 为真值，则 \([x]_反\) 为反码
如，设 \(x=1100110\)，则 \([x]_反=01100110\)
设 \(x=-1100110\)，则 \([x]_反=10011001\)

反码可表示的范围（\(n\) 位二进制）： \(-(2^{n-1}-1) \sim 2^{n-1}-1\)（不存在无符号情况）
如8位二进制，表示范围为 \(-127 \sim 127\)

#4.3 补码

在计算机系统中，数值一律用补码来表示和存储。原因在于，使用补码，可以将符号位和数值域统一处理；同时，加法和减法也可以统一处理

  • 当原码为正数时，补码与原码一致
  • 当原码为负数时，补码是反码加一。
  • \(0\) 只有一种表示方法，\([+0]_补=[-0]_补=000...0\)

设 \(x\) 为真值，则 \([x]_补\) 为补码
如，设 \(x=1100110\)，则 \([x]_补=01100110\)
设 \(x=-1100110\)，则 \([x]_补=10011010\)

补码可表示的范围（\(n\) 位二进制）： \(-2^{n-1} \sim 2^{n-1}-1\)（不存在无符号情况）
如8位二进制，表示范围为 \(-128 \sim 127\)（\(10000000\) 的值为 \(-128\)，\(11111111\) 的值为 \(-1\)）

#4.4 关于补码加法和减法也可以统一处理的解释

先介绍一下“模”的概念：“模”是指一个计量系统的计数范围，如过去计量粮食用的斗、时钟等。计算机也可以看成一个计量机器，因为计算机的字长是定长的，即存储和处理的位数是有限的，因此它也有一个计量范围，即都存在一个“模”。如：时钟的计量范围是 \(0 \sim 11\)，模= \(12\)。表示n位的计算机计量范围是 \(0 \sim 2^n -1\)，模= \(2^n\)．“模”实质上是计量器产生“溢出”的量，它的值在计量器上表示不出来，计量器上只能表示出模的余数。任何有模的计量器，均可化减法为加法运算。就是取反后加1。
——摘自补码_百度百科

假设当前时针指向8点，而准确时间是6点，调整时间可有以下两种拨法：

  • 一种是倒拨2小时，即 \(8-2=6\)
  • 一种是顺拨10小时，\(8+10=12+6=6\)，即 \(8-2=8+10=8+12-2 (\mod 12)\)

在12为模的系统里，加10和减2效果是一样的，因此凡是减2运算，都可以用加10来代替。若用一般公式可表示为：\(a-b=a-b+mod=a+(mod-b)\)。对“模”而言，2和10互为补数。实际上，以12为模的系统中，11和1，8和4，9和3，7和5，6和6都有这个特性，共同的特点是两者相加等于模。对于计算机，其概念和方法完全一样。n位计算机，设n=8，所能表示的最大数是 \(11111111\)，若再加1成 \(100000000\)(9位)，但因只有8位，最高位1自然丢失。又回到了 \(00000000\)，所以8位二进制系统的模为 \(2^8\)。在这样的系统中减法问题也可以化成加法问题，只需把减数用相应的补数表示就可以了。把补数用到计算机对数的处理上，就是补码

#4.5 补码求原码

已知一个数的补码，求原码的操作其实就是对该补码再求补码：

  • 如果补码的符号位为“0”，表示是一个正数，其原码就是补码。
  • 如果补码的符号位为“1”，表示是一个负数，那么求给定的这个补码的补码就是要求的原码。

例：已知一个补码为 \(11111001\)，则原码是 \(00000111(-7)\)。
因为符号位为“1”，表示是一个负数，所以该位不变，仍为“1”。
其余七位 \(1111001\) 取反后为 \(0000110\)；再加1，所以是 \(00000111\)。

#4.6 例题

NOIP 2017 普及组初赛试题第1题

在 8 位二进制补码中，10101011 表示的数是十进制下的（ ）。
 A. 43
 B. -85
 C. -43
 D. -84

先将补码转换为原码，已知补码求原码，就是将这个补码再求补码
而符号位为1，说明为负数，则除符号位外，按位取反，再加一
得：11010101
转化为十进制为 -85
故选 B

#5.0 逻辑运算

注：这里讲的是数学布尔运算

逻辑运算符：

  • \(\lnot\) （逻辑非）
  • \(\land\) （逻辑与）
  • \(\lor\) （逻辑或）
  • \(1\) 和 \(0\) 表示 “真” 和 “假”

#5.1 运算级比较

\(\lnot(非) > \land(与) > \lor(或)\)
若有括号先算括号内的，同级运算由左向右

#5.2 运算规则

  • \(\lnot\) 之后的若为真，则为假；若为假，则为真。简单来讲，就是取反
  • \(\land\) 左右两者都为真，则为真，否则为假
  • \(\lor\) 左右两者有一者及以上为真，则为真，否则为假

#6.0 位运算

程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。

位运算符

  • \(\& (and)\) （按位与）
  • \(|(or)\) （按位或）
  • \(\hat{} (xor)\) （按位异或）

#6.1 运算级比较

\(\& (与) > \hat{} (异或) > |(或)\)
若有括号先算括号内的，同级运算由左向右

#6.2 运算规则

注：以下运算规则都是将数字转为二进制后对于每一位的运算

  • \(\&\) 两者都为 \(1\)，则为 \(1\)，否则为 \(0\)
  • \(\hat{}\) 两者不同（一 \(1\) 一 \(0\)），则为 \(1\)，否则为 \(0\)
  • \(|\) 两者有一者及以上为 \(1\)，则为 \(1\)，否则为 \(0\)

例：

\[\begin{align*} \fbox{22 & 5}\\ 22:1011 & 0\\ \quad 5:0010 & 1\\ \hline 0010 & 0\\ 00100=4 \end{align*}\]

所以 \(22 \& 5=4\)

\[\begin{align*} \fbox{22 ^ 4}\\ 22:1011 & 0\\ \quad 4:0010 & 0\\ \hline 1001 & 0\\ 10010=18 \end{align*}\]

所以 \(22 \hat{} 4=18\)

\[\begin{align*} \fbox{22 | 5}\\ 22:1011 & 0\\ \quad 5:0010 & 1\\ \hline 1011 & 1\\ 10111=23 \end{align*}\]

所以 \(22 | 5=23\)

#7.0 数据结构

#7.1 栈

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

栈的特点：后入先出

#7.2 队列

队列的特点：先入先出

#7.3 二叉树

性质

  • 在二叉树的第 \(i\) 层上最多有 \(2^{i-1}\) 个节点(\(i \geqslant 1\))
  • 深度为 \(k\) 的二叉树至多有 \(2^k-1\) 个节点(\(k \geqslant 1\))
  • 对任意一棵二叉树，如果其叶节点数为 \(n_0\) ，度为 \(2\) 的节点数为 \(n_2\) ，则一定满足：\(n_0 = n_2 + 1\)
  • 具有 \(n\) 个节点的完全二叉树的深度为 \(\lfloor \log_{2}n \rfloor + 1\)
  • 对于一棵 \(n\) 个节点的完全二叉树，对任意一个节点(编号为 \(i\))，有：
    • 如果 \(i=1\)，则节点 \(i\) 为根，无父节点
    • 如果 \(i>1\)，则其父结点编号为 \(\dfrac{i}{2}\)，
    • 如果 \(2 \times i > n\)，则结点 \(i\) 无左右儿子，为叶结点，否则左儿子编号为 \(2 \times i\)
    • 如果 \(2 \times i + 1 > n\)，则结点 \(i\) 无右儿子，否则右儿子编号为 \(2 \times i + 1\)

#7.4 线段树

本人曾写过一篇讲线段树的文章，这里便不再赘述，有兴趣的可以点击下方传送门进入

#8.0 数学问题

推销大佬博客（自己懒）

#9.0 其他

#9.1 图片大小计算

公式

\(图片大小=\dfrac{分辨率（长 \times 宽） \times 位深}{8}\)

例题

如有一张分辨率为 \(4096 \times 2160\) ，每一像素都是 \(24\) 位真彩色，则图片大小大约是：
A. 8MB
B. 25MB
C. 200MB
D. 200KB
这张图片的大小为：

\[\begin{align*} &\dfrac{4096 \times 2160 \times 24}{8} B\\ =&(1024 \times 1080 \times 24) B\\ =&(1080 \times 24) KB\\ \approx & 25MB \end{align*}\]

选 B

#9.2 哈夫曼编码

哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码（有时也称为霍夫曼编码）。 ——百度百科·哈夫曼编码

比如说，我们有 \(4\) 种字符，分别为 \(a\)，\(b\)，\(c\)，\(d\)，分别出现的次数是 \(20\) 次，\(50\) 次，\(5\) 次，\(25\) 次
构建哈夫曼编码时先计算每个字符出现的概率，得到：
\(P(a)=\dfrac{1}{5}\)
\(P(b)=\dfrac{1}{2}\)
\(P(c)=\dfrac{1}{20}\)
\(P(d)=\dfrac{1}{4}\)
然后按照大小进行排序

然后取概率最小的两个符号开始，可选其中一个支路为0，另一支路为1。这里，我们选上支路为0，下支路为1。将两支路的概率合并，并重新排队

依次类推，概率并为1，最终可得下图

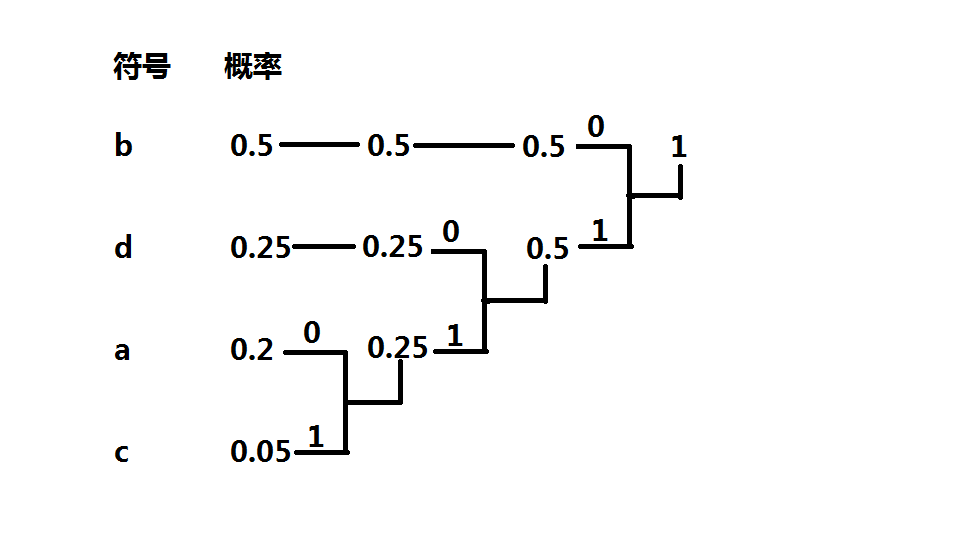
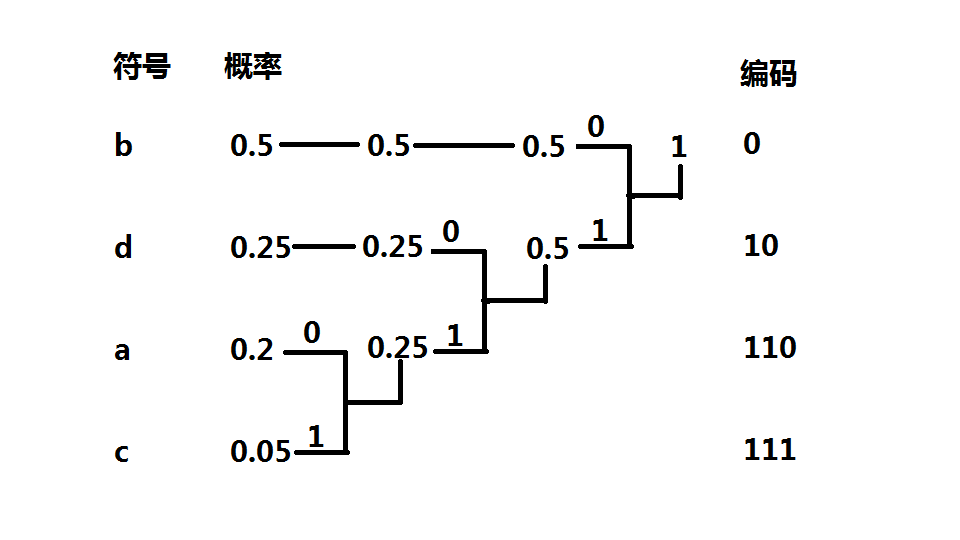
从概率1到单个字符的概率的路径上的0或1组合就成了该字符的编码

更新日志及说明

更新

个人主页

欢迎到以下地址支持作者！
Github：戳这里
Bilibili：戳这里
Luogu：戳这里

posted @ 2020-10-08 17:22  Dfkuaid  阅读(1088)  评论(3)  编辑  收藏  举报