[字符串入门]KMP算法
引入
现在我们面临这样一个问题:有一个主串S,和一个模式串P,现在要查找P在S中的位置,怎么查找呢?
Brute-Force(暴力求解)
思路
如果用暴力匹配的思路,并假设现在主串S匹配到 i 位置,模式串P匹配到 j 位置,则有:
- 如果当前字符匹配成功(即\(S_i = P_{j}\)),则\(i++,j++\),继续匹配下一个字符;
- 如果失配(即\(S_i \not= P_j\)),令\(i = i - (j - 1),j = 0\)。相当于每次匹配失败时,i 回溯,j 被置为0。
举个例子,我们有一个主串\(AAAAAAB\),我们要查找模式串\(AAAB\)的位置,则过程如下图:
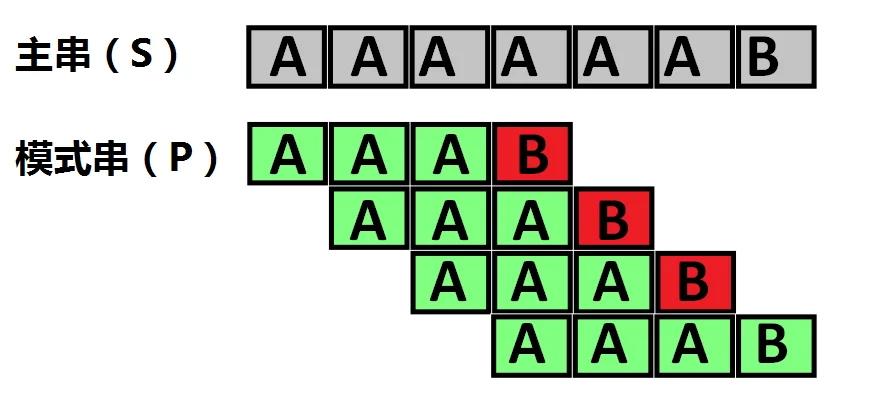
代码
int Brute-Force(string s,string p) {
int ls = s.length();
int lp = p.length();
int i = 0;
int j = 0;
while (i < ls && j < lp){
if (s[i] == p[j]){
//如果当前字符匹配成功则i++,j++
i++;
j++;
}
else {
//如果失配,令i = i - (j - 1),j = 0
i = i - j + 1;
j = 0;
}
}
//匹配成功,返回模式串p在文本串s中的位置,否则返回-1
if (j == lp)
return i - j;
else
return -1;
}
我们成功实现了 Brute-Force 算法。现在,我们看一下它的时间复杂度。记 \(n = |S|\) 为串 S 的长度,\(m = |P|\) 为串 P 的长度。不难想到 Brute-Force 算法所面对的最坏情况:主串形如\(AAAAAAAAAAA...B\),而模式串形如\(AAAAA...B\)。每次字符串比较都需要付出 \(|P|\)次字符比较的代价,总共需要比较 \(|S| - |P| + 1\) 次,因此总时间复杂度是\(O(|P| \cdot (|S| - |P| + 1))\). 考虑到主串一般比模式串长很多,故 Brute-Force 的复杂度是\(O(|P| \cdot |S|)\),也就是 \(O(nm)\)的。u1s1,我家门口的蜗牛跑的都比他快...
KMP算法
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为Knuth-Morris-Pratt操作(简称KMP算法)。
从改进暴力算法开始
分析暴力算法,我们发现,我们很难降低字符串比较的复杂度,因此,我们考虑降低比较的次数。如果比较的趟数能降到足够低,那么总的复杂度也将会下降很多。
看下面这个例子:
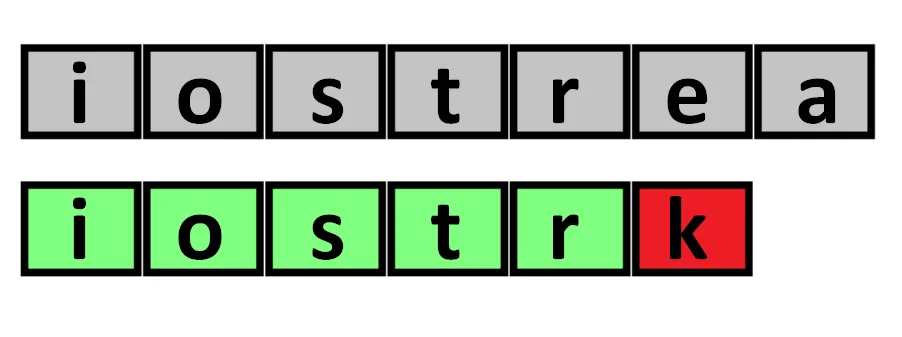
在 Brute-Force 中,如果从 S[i] 开始的那一趟比较失败了,会直接开始尝试从 S[i+1] 开始比较。我们应当注意到,一次失败的匹配,会给我们提供宝贵的信息——如果 \(S\) 与 \(P\) 的匹配是在第 \(r\) 个位置失败的,那么从 S[i] 开始的 \((r-1)\) 个连续字符,一定与 P 的前 \((r-1)\) 个字符是一样的!
例如:
可以发现,是在 \(P[5]\) 失配的,那么说明 \(S[0:5]\) 等于 \(P[0:5]\),即 \(ABCAB\). 现在我们来考虑:从 \(S[1]\)、\(S[2]\)、\(S[3]\) 开始的匹配,有没有可能成功?
这里\(K[n:m]\)使用了\(Python\)的语法,表示\(K[n] \sim K[m - 1]\)
从 \(S[1]\) 开始肯定没办法成功,因为 \(S[1] = P[1] = 'B'\),和 \(P[0]\) 并不相等。从 \(S[2]\) 开始也不行,因为 \(S[2] = P[2] = 'C'\),并不等于\(P[0]\). 但是从 \(S[3]\) 开始是有可能成功的。
KMP的精髓——next数组
P 的 next[i] 表示 P[0] ~ P[i - 1] 这一个子串中,前k个字符恰等于后k个字符的最大的k,也就是代表当前字符之前的字符串中,有多大长度的相同前缀后缀。
如\(P=ABCABE\),当\(i=4\)时,next[4] = 1,也就是子串\(A\),当\(i=5\)时,next[5] = 2,也就是子串\(AB\)。
在使用暴力算法时,每次仅将模式串向后移动一位,而改进算法则是一下移动好几位,跳过那些不可能匹配成功的位置,由 3.1 节可以发现旧的\(P\)已匹配的部分的后缀要与\(P\)的前缀一致(假设\(P\)在\(i\)处失配,那么已匹配部分即为\(P[0] - P[i - 1]\)),也就是要求\(P[0] \sim P[i - 1]\)中有多大长度的相同前缀后缀,这不正是next数组吗!
存储字符串时,第一个字符对应的下标是\(0\),而\(next[i]\)存储的是长度,也就是说,最大长度的相同前缀后缀中的前缀的最后一个字符的下标为\(next[i] - 1\),那么\(next[i]\)作为下标对应的字符为最大长度的相同前缀后缀中的前缀的最后一个字符的下一个,也就是并不属于\(P[0] - P[i - 1]\)最大长度的相同前缀后缀中的前缀的第一个字符
假设现在\(S\)匹配到\(i\)位置,\(P\)匹配到\(j\)位置
- 如果\(j = -1\),或者当前字符匹配成功都令
i++;j++,继续匹配下一个字符; - 如果\(j \not= -1\),且当前字符匹配失败,则令\(i\)不变,
j = next[j]。此举意味着失配时,模式串\(P\)相对于文本串\(S\)向右移动了\(j - next [j]\) 位,此时将\(S[i]\)与\(P[next[j]]\)比较(由前面的分析可以得到,失配时,前面的子串相等),重复这一步,直至满足\(j = -1\)或\(s[i] = p[j]\)。
由此,我们可以得到以下代码:
void KmpSearch(string s,string p) {
int ls = s.length();
int lp = p.length();
int j = 0;
for(int i = 0;i < ls;i ++){
while(j != -1 && p[j] != s[i])
j = next[j];
j ++;
if (j == lp){
cout << i - lp + 2 << endl;
j = next[j];
}
}
}
快速求得next数组
这是最后一个问题,也是最重要的——如何快速构建next数组。快速构建next数组,核心思想是“P自己与自己做匹配”。
回顾next数组: \(next[x]\) 定义为: \(P[0] \sim P[x]\) 这一段字符串,使得长度为\(k\)的前缀恰等于长度为\(k\)的后缀的最大的\(k\)(\(k\)不能等于自身长度)。那么,我们可以考虑,从\(P\)串的头开始,逐个比较,由于前缀或后缀的长度都不能等于这个串的本长,两个比较字符最近时也只是相邻,故初始head = -1,tail = 0(\(head\)表示前缀,\(tail\)表示后缀)
分情况讨论。
-
如果\(head = -1\),则说明未开始或\(P[0] \sim P[tail]\)没有相同前后缀,
head ++;tail++;next[tail] = head; -
如果\(P[head] = P[tail]\),两个字符相同,此时\(P[0] \sim P[tail]\)最长相同前后缀的长度为\(head + 1\),也就是说,\(next[tail + 1] = head + 1\),将两个指针后移指向下一位,
head ++;tail ++; -
否则\(P[head] \not= P[tail]\),两个字符不相同,由于 \(head\) 一定小于 \(tail\),此时\(next[head]\)必定是已知的,则令\(tail\)不变,
head = next[head];,跳回到\(P[0] \sim P[head - 1]\)中最长相同前后缀的下一位,此时将\(P[tail]\)与\(P[next[head]]\)比较(\(head\)为执行head = next[head];前),重复这一步,直至满足\(head = -1\)或\(P[head] = P[tail]\)。
这与原问题处理很相似,主串\(S'\)为\(P\)串本身,模式串\(P'\)为\(P[0] \sim P[head]\),与 3.2 节中思想相同,旧的\(P[0] - P[head]\)的已匹配的部分的后缀要与\(P[0] \sim P[head]\)前缀一致,才可以将\(P[0] \sim P[head]\)这把“标尺”向后跳跃式移动
void GetNext(string p,int next[]) {
int lp = p.length();
next[0] = -1;
int head = -1;
for(int tail = 0;tail < lp;tail ++){
while (head != -1 && p[tail] != p[head])
head = next[head];
head ++;
next[tail + 1] = head;
}
}
求得next数组的优化
按照以上的方法求解next数组,会有一个小问题,如:
\(S="ABACABAB"\)
\(P="ABAB"\)
\(next = \{ -1,0,0,1 \}\)
当\(i = 3\)且\(j = 3\)时,B与C失配,j = next[j],此时\(j = 1\),B和C将再一次失配;那么,我们发现,如果\(p[j] = p[next[j]]\),必然导致后一步匹配失败(因为\(p[j]\)已经跟\(s[i]\)失配,用跟\(p[j]\)等同的值\(p[next[j]]\)去跟\(s[i]\)匹配必然失配)。如果出现了\(p[j] = p[next[j]]\),我们直接使\(j\)跳回\(next[next[j]]\),即在求next数组时,在 \(p[tail] = p[head]\) 的前提下,若 \(p[tail + 1] = p[head + 1]\) 运行next[tail + 1] = next[head + 1](\(next[head + 1]\)与\(next[next[tail]]\)必定相等)。
那么,可以得到以下修改后的代码:
void GetNext(string p,int next[]) {
int lp = p.length();
next[0] = -1;
int head = -1;
int tail = 0;
while (tail < lp){
//p[head]表示前缀,p[tail]表示后缀
if (head == -1 || p[tail] == p[head]){
++ head;
++ tail;
if (p[head] != p[tail])
next[tail] = head;
else
next[tail] = next[head];
}
else
head = next[head];
}
}
这样得到的next数组:
\(next=\{ -1,0,-1,0 \}\)
此时应当使用的KmpSearch:
void KmpSearch(string s,string p) {
int ls = s.length();
int lp = p.length();
int i = 0;
int j = 0;
while (i < ls){
if (j == -1 || s[i] == p[j]){
i++;
j++;
}
else
j = next[j];
if (j == lp)
cout << i - j + 1 << endl;
}
}
时间复杂度分析
我们发现如果某个字符匹配成功,模式串首字符的位置保持不动,仅仅是 i ++、j ++;如果匹配失配,\(i\) 不变,模式串会跳过匹配过的\(next[j]\)个字符,这样的运算时间复杂度都是\(O(1)\)的。整个算法最坏的情况是,当模式串首字符位于\(i - j\)的位置时才匹配成功,算法结束。
所以,如果文本串的长度为\(n\),模式串的长度为\(m\),那么匹配过程的时间复杂度为\(O(n)\),算上计算next的\(O(m)\)时间,KMP的整体时间复杂度为\(O(m + n)\)。
练习
模板
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int next[10001];
string s,p;
void GetNext(string p,int next[]) {
int lp = p.length();
next[0] = -1;
int head = -1;
for(int tail = 0;tail < lp;tail ++){
while (head != -1 && p[tail] != p[head])
head = next[head];
head ++;
next[tail + 1] = head;
}
}
void KmpSearch(string s,string p) {
int ls = s.length();
int lp = p.length();
int j = 0;
for(int i = 0;i < ls;i ++){
while(j != -1 && p[j] != s[i])
j = next[j];
j ++;
if (j == lp){
cout << i - lp + 2 << endl;
j = next[j];
}
}
}
int main() {
cin >> s >> p;
GetNext(p,next);
KmpSearch(s,p);
for (int i = 1;i <= p.length();i ++)
cout << next[i] << " ";
return 0;
}
更新日志及说明
更新
- 初次完成编辑 - \(2020.6.30\)
本文若有更改或补充会持续更新


