2016-2017 ACM-ICPC Northeastern European Regional Contest Problem E. Expect to Wait

题目来源:http://codeforces.com/group/aUVPeyEnI2/contest/229509
时间限制：2s
空间限制：512MB
题目大意：
在一个车站中有若干人在队列中等待车辆，求所有人等待时间的期望值
首先给定n和q，随后是n行操作:
"+ t k":在t时刻有k个人加入队列等待车辆
"- t k":在t时刻有k个人乘车离开队列
然后是q个数字代表在初始时刻车站中有多少个车在等待
求出每个询问对应的所有人的等待时间，如果有人始终等不到车则输出"INFINITY"
样例：

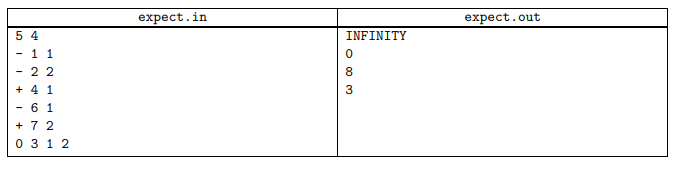
代码：

#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <cstdio>
#include <string>
#include <cmath>
#include <queue>
#include <set>
#include <map>
#include <complex>
using namespace std;
typedef long long ll;
typedef long double db;
typedef pair<int,int> pii;
typedef vector<int> vi;
#define de(x) cout << #x << "=" << x << endl
#define rep(i,a,b) for(int i=(a);i<(b);i++)
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define pi acos(-1.0)
#define mem0(a) memset(a,0,sizeof(a))
#define memf(b) memset(b,false,sizeof(b))
#define ll long long
#define eps 1e-10
#define inf 1e17
#define maxn 101010
int n, q;
int a[maxn], t[maxn];
int s[maxn];
int b[maxn], cnt;
long long ans[maxn];
struct node{
    int x, id;
    bool operator < (const node &rhs) const{
        return x < rhs.x;
    }
}c[maxn];
bool cmp(int i, int j){
    return s[i] > s[j];
}

int main()
{
    freopen("expect.in", "r", stdin);
    freopen("expect.out", "w", stdout);
    scanf("%d%d", &n, &q);
    for(int i = 1; i <= n; i++){
        char op[5];
        scanf("%s%d%d", op, &t[i], &a[i]);
        if(op[0] == '-') a[i] = -a[i];
    }
    for(int i = 1; i <= n; i++){
        s[i] = s[i-1] + a[i];
        if(i < n) t[i] = t[i+1] - t[i];
    }
//    for(int i = 1; i <= n; i++){
//        printf("s[%d] = %d, t[%d] = %d\n", i, s[i], i, t[i]);
//    }
    long long sum1 = 0, sum2 = 0;
    for(int i = 1; i <= n; i++){
        if(s[i] < 0){
            b[++cnt] = i;
            sum1 += 1LL*(-s[i])*t[i];
            sum2 += t[i];
        }
    }
    sort(b + 1, b + cnt + 1, cmp);
    int j = 1;
    long long k = 0;
    for(int i = 1; i <= q; i++){
        scanf("%d", &c[i].x);
        c[i].id = i;
    }
    sort(c + 1, c + q + 1);
    for(int i = 1; i <= q; i++){
        int x = c[i].x;
        while(j <= cnt && (-s[b[j]]) <= x){
            sum1 -= 1LL*(-s[b[j]]) * t[b[j]];
            sum2 -= t[b[j]];
            ++j;
        }
        if(s[n] + x < 0){
            ans[c[i].id] = -1;
        }
        else{
            ans[c[i].id] = sum1 - x * sum2;
        }
    }
    for(int i = 1; i <= q; i++){
        if(ans[i] == -1) printf("INFINITY\n");
        else printf("%lld\n", ans[i]);
    }
    return 0;
}