BZOJ-1089 [SCOI2003]严格n元树(dp+大数)

题目描述

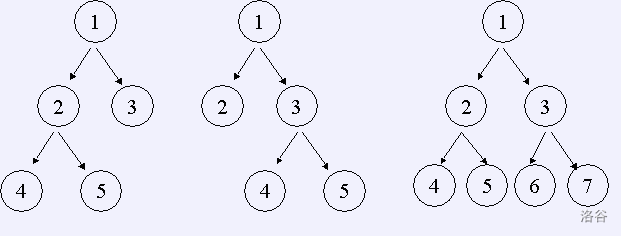
  如果一棵树的所有非叶节点都恰好有 \(n(1\leq n\leq 32)\) 个儿子，那么我们称它为严格 \(n\) 元树。如果该树中最底层的节点深度为 \(d(0\leq d\leq 16)\)（根的深度为 \(0\)），那么我们称它为一棵深度为 \(d\) 的严格 \(n\) 元树。例如，深度为 \(2\) 的严格 \(2\) 元树有三个，如下图：

分析

  设 \(dp[i]\) 为深度不超过 \(i\) 的严格 \(n\) 元树的数量。考虑如何转移，新建一个根节点，根节点有 \(n\) 个儿子，每个儿子都可以挂一个子树，方案数为 \(dp[i-1]\)，或者每个儿子都不挂子树。则状态转移方程为：

\[dp[i]=dp[i-1]^n+1 \]

  答案为 \(dp[d]-dp[d-1]\)。

代码

n,d=map(int,input().strip().split())
dp=[1]
for i in range(1,d+1):
    dp.append(dp[i-1]**n+1)
if(d==0):
    print(1)
else :
    print(dp[d]-dp[d-1])