BZOJ-1965 [Ahoi2005]SHUFFLE 洗牌(exgcd)

题目描述

  对于扑克牌的一次洗牌是这样定义的，将一叠 \(n\)（\(n\) 为偶数）张扑克牌平均分成上下两叠，取下面一叠的第一张作为新的一叠的第一张，然后取上面一叠的第一张作为新的一叠的第二张，再取下面一叠的第二张作为新的一叠的第三张 \(\cdots\) 如此交替直到所有的牌取完。

  如果对一叠 \(6\) 张的扑克牌 \([1,2,3,4,5,6]\)，进行一次洗牌的过程如下图所示：

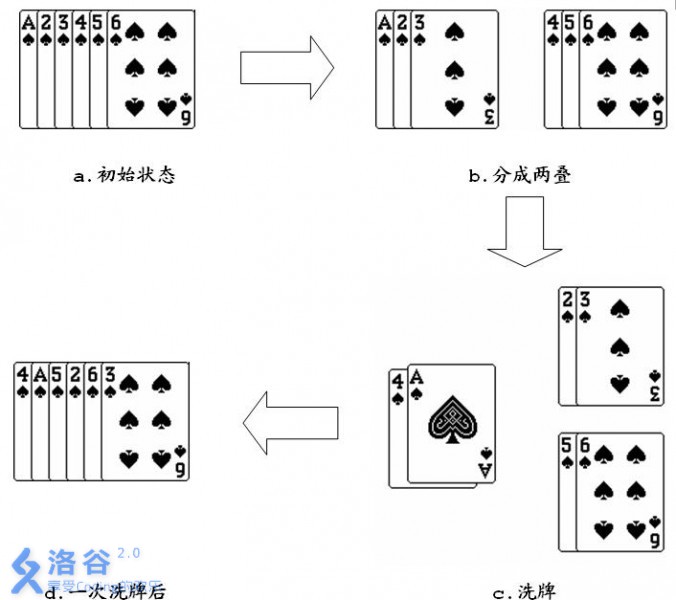
  从图中可以看出经过一次洗牌，序列 \([1,2,3,4,5,6]\) 变为 \([4,1,5,2,6,3]\)。当然，再对得到的序列进行一次洗牌，又会变为 \([2,4,6,1,3,5]\)。

  游戏是这样的，如果给定长度为 \(n\) 的一叠扑克牌，并且牌面数字从 \(1\) 开始连续增加到 \(n\)（不考虑花色），对这样的一叠扑克牌，进行 \(m\) 次洗牌，求经过洗牌后的扑克牌序列中第 \(k\) 张扑克牌的牌面数字大小。

  数据范围：\(0<n\leq 10^{10},0\leq m\leq 10^{10},n\) 为偶数。

分析

  假设初始的序列为 \([1,2,3,4,5,6,7,8,9,10]\)，一次洗牌后变成 \([6,1,7,2,8,3,9,4,10,5]\)。

  可以发现 \(1,2,3,4,5\) 的位置分别变成了 \(2,4,6,8,10\)，即变成了原来的二倍；\(6,7,8,9,10\) 的位置分别变成了 \(1,3,5,7,9\)。即扑克 \(x\) 的位置变成了 \(2x \mod {(n+1)}\)。

  继续洗牌，序列 \([6,1,7,2,8,3,9,4,10,5]\) 变成了 \([3,6,9,1,4,7,10,2,5,8]\)，每张扑克 \(x\) 的位置变成了 \(4x\mod {(n+1)}\)（和原序列相比）。

  归纳一下，经过 \(m\) 轮洗牌后，扑克 \(x\) 的位置变成了 \(2^m x\mod {(n+1)}\)。

  欲求第 \(k\) 张牌的原始位置，可以列出同余方程 \(2^{m}x\equiv k\pmod {n+1}\)。

  转化为 \(2^mx+(n+1)y=k\Longrightarrow 2^m\frac{x}{k}+(n+1)\frac{y}{k}=1\)。

  扩展欧几里得算法求出 \(\frac{x}{k}\)，再乘 \(k\) 即可得到原位置 \(x\)。

代码

#include<bits/stdc++.h>
using namespace std;
long long n,m,k;
long long quick_mul(long long a,long long b,long long mod)
{
    long long ans=0;
    while(b)
    {
        if(b&1)
            ans=(ans+a)%mod;
        a=(a+a)%mod;
        b>>=1;
    }
    return ans%mod;
}
long long quick_pow(long a,long long b,long long mod)
{
    long long ans=1;
    while(b)
    {
        if(b&1)
            ans=quick_mul(ans,a,mod);
        a=quick_mul(a,a,mod);
        b>>=1;
    }
    return ans%mod;
}
long long exgcd(long long a,long long b,long long &x,long long &y)
{
    if(!b)
    {
        x=1;
        y=0;
        return a;
    }
    long long gcd=exgcd(b,a%b,y,x);
    y=y-x*(a/b);
    return gcd;
}
int main()
{
    cin>>n>>m>>k;
    long long x,y;
    exgcd(quick_pow(2,m,n+1),n+1,x,y);
    x=(x%(n+1)+(n+1))%(n+1);
    cout<<quick_mul(x,k,(n+1))<<endl;
    return 0;
}