BZOJ-1433 [ZJOI2009]假期的宿舍(最大流)

题目描述

  有些同学回家了，而有些同学则有以前的好朋友来探访，那么住宿就是一个问题。比如 \(A\) 和 \(B\) 都是学校的学生，\(A\) 要回家，而 \(C\) 来看 \(B\)，\(C\) 与 \(A\) 不认识。假设每个人只能睡和自己直接认识的人的床。那么一个解决方案就是 \(B\) 睡 \(A\) 的床而 \(C\) 睡 \(B\) 的床。而实际情况可能非常复杂，有的人可能认识好多在校学生，在校学生之间也不一定都互相认识。已知一共有 \(n(1\leq n\leq 50)\) 个人，并且知道其中每个人是不是本校学生，也知道每个本校学生是否回家。问是否存在一个方案使得所有不回家的本校学生和来看他们的其他人都有地方住。

分析

  \(1.\) 把每个人看成左部点，编号 \(1\) ~ \(n\)；每张床看成右部点 \(n+1\) ~ \(2n\)。

  \(2.\) 所有本校学生的床向汇点 \(T\) 连边，外校人的床不连边（因为根本不存在）。

  \(3.\) 不回家的本校学生和外校人向源点 \(S\) 连边，回家的本校学生不连边（因为他不需要床），记录需要床的人数 \(cnt\)。

  \(4.\) 假设人 \(i\) 认识人 \(j\)，则把人 \(i\) 与床 \(j+n\) 连边；人 \(i\) 向自己的床 \(i+n\) 连边。

  如果最大流等于 \(cnt\)，则存在方案，否则不存在。

  样例建图如下：

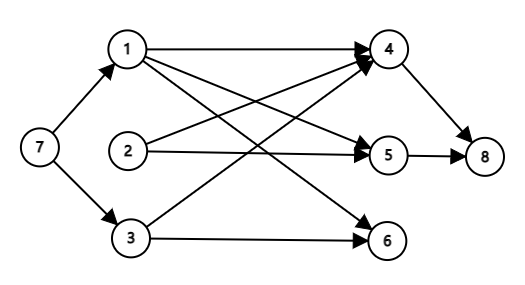
  \(S\rightarrow1\rightarrow 5\rightarrow T\) 代表 \(1\) 睡 \(2\) 的床，\(S\rightarrow 3\rightarrow 4\rightarrow T\) 代表 \(3\) 睡 \(1\) 的床。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=1010,M=20010;
const int INF=0x3f3f3f3f;
int a[110];
int n,m,S,T,num_edge,head[N];
struct Edge
{
    int to;
    int Next;
    int dis;
}edge[M];
void add_edge(int from,int to,int dis)
{
    edge[++num_edge].to=to;
    edge[num_edge].dis=dis;
    edge[num_edge].Next=head[from];
    head[from]=num_edge;
}
queue<int> Q;
int d[N];
bool bfs()
{
    memset(d,0,sizeof(d));
    while(!Q.empty())
        Q.pop();
    Q.push(S);
    d[S]=1;
    while(!Q.empty())
    {
        int x=Q.front();
        Q.pop();
        for(int i=head[x];i;i=edge[i].Next)
        {
            int y=edge[i].to;
            if(edge[i].dis&&!d[y])
            {
                Q.push(y);
                d[y]=d[x]+1;
                if(y==T)
                    return 1;
            }
        }
    }
    return 0;
}
int Dinic(int x,int flow)
{
    if(x==T)
        return flow;
    int rest=flow,k;
    for(int i=head[x];i&&rest;i=edge[i].Next)
    {
        int y=edge[i].to;
        if(edge[i].dis&&d[y]==d[x]+1)
        {
            k=Dinic(y,min(rest,edge[i].dis));
            if(k==0)
                d[y]=0;
            edge[i].dis-=k;
            edge[i^1].dis+=k;
            rest-=k;
        }
    }
    return flow-rest;
}
int main()
{
    int _;
    cin>>_;
    while(_--)
    {
        num_edge=1;
        int n;
        cin>>n;
        memset(head,0,sizeof(head));
        int cnt=0;
        S=n+n+1;T=n+n+2;
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            if(a[i]==1)
            {
                add_edge(i+n,T,1);
                add_edge(T,i+n,0);
            }
        }
        for(int i=1;i<=n;i++)
        {
            int x;
            scanf("%d",&x);
            if(a[i]==0||(a[i]==1&&x==0))
            {
                add_edge(S,i,1);
                add_edge(i,S,0);
                cnt++;
            }
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                int x;
                scanf("%d",&x);
                if(x==1||i==j)
                {
                    add_edge(i,j+n,1);
                    add_edge(j+n,i,0);
                }
            }
        }
        int maxflow=0,flow=0;
        while(bfs())
        {
            flow=Dinic(S,INF);
            maxflow+=flow;
        }
        if(maxflow==cnt)
            puts("^_^");
        else
            puts("T_T");
    }
    return 0;
}