机器学习基石笔记2——在何时可以使用机器学习(2)
2 Learning to Answer Yes/No
2.1 Perceptron Hypothesis Set
根据信用卡问题引入PLA算法。
有以下特征:
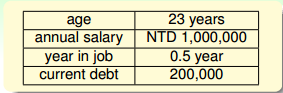
抽象一下,成为特征向量x,根据x和权重的w的内积相对于阈值的大小决定输出标签的正负(正则赋予信用卡,负不赋予信用卡):

具体而言,感知机(perceptron)的假设空间如下: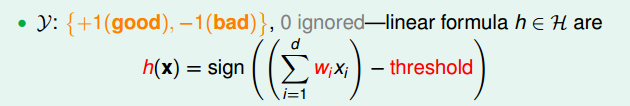
sign又叫sgn: 当x<0时,sign(x)=-1;当x=0时,sign(x)=0;当x>0时,sign(x)=1。
感知机的假设空间的向量形式:权重向量w和特征向量x的内积=|w|*|x|*cos(Θ)。

x0=1,w0=阈值的相反数。
再具体到二维的Perceptrons:
注意到输出空间是二值的,+1赋予信用卡(红圈圈),-1不赋予信用卡(蓝叉叉)。
实际上,感知机的假设是空间上的一个个超平面。所以,感知机是线性分类器。

做道题:
解答:

2.2 Perceptron Learning Algorithm (PLA)
介绍PLA的具体内容。

本质上PLA是一个在训练集D上不断发现错误,纠正错误的过程。一直到遍历所有实例点,没有被分类错误的点时,算法停止,返回权重向量w。
1. 初始化权重w为w0(w0=0)。
2. 按照顺序序列或者随机序列(考虑方便性,一般是顺序序列),遍历训练集D中的点,找被分类错的点。如果有,纠正w。
3. 重复1和2,直到遍历所有训练样本没有被误分类的点,算法停止。
这里要注意:2中纠正w以后,w接下去遍历剩下的点,而不是重新开始遍历训练集D。
参考:https://class.coursera.org/ntumlone-003/forum/thread?thread_id=164
这里解释算法的步骤2中纠正w:
如果sign()=-1,但是y=+1,也就是说w和x的夹角过大,需要将w向x扳回一些:wt+yn(t)xn(t)相当于上图右上。
如果sign()=+1,但是y=-1,也就是说w和x的夹角过小,需要将w向x扳出一些:wt+yn(t)xn(t)相当于上图右下。
老师的ppt上有关于二维PLA的一个具体运行过程。

权重向量w垂直于分类线。
证明:
方法一:图中的分类线是3维上,以w为法向量的平面与平面上任一点满足w0+w1x1+w2x2=0的平面(1,x1,x2)相交形成的。因此,权重向量w自然垂直于该相交线,也就是垂直于分类线。
方法二:线上任意2个3维点a,b都满足方程wTx=0,那么有wTxa=wTxb=0,所以 wT(xa−xb)=0,也就是说,w 垂直于过a,b的直线。
上面的2个想法可以推广到高维。
参考:https://class.coursera.org/ntumlone-003/forum/thread?thread_id=13
这里有2个问题:
1. PLA的算法一定能停下来吗?
2. 假设能停下来,得到的g与真实的f 到底是否一样?
做道题:
解答:

2.3 Guarantee of PLA
PLA算法一定能停下来。
结论:
证明:
1. 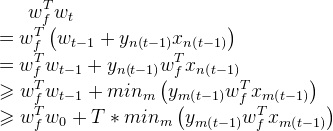
2. 
3. w0=0(w0也必须为0)。
由1可知 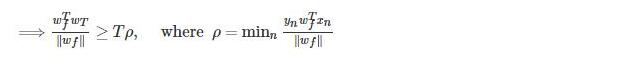
由2可知 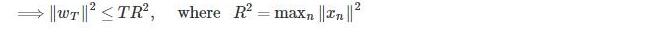
所以 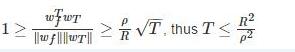
参考:https://class.coursera.org/ntumlone-003/forum/thread?thread_id=8
LaTeX中的公式编辑代码:
w_{f}^{T}w_{t} \\
= w_{f}^{T}\left ( w_{t-1}+y_{n\left (t-1\right )}x_{n\left (t-1\right )} \right ) \\
= w_{f}^{T} w_{t-1}+y_{n\left (t-1\right )} w_{f}^{T} x_{n\left (t-1\right )} \\
\geqslant w_{f}^{T} w_{t-1}+ min_{m} \left ( y_{m\left (t-1\right )} w_{f}^{T} x_{m\left (t-1\right )} \right ) \\
\geqslant w_{f}^{T} w_{0}+T*min_{m} \left ( y_{m\left (t-1\right )} w_{f}^{T} x_{m\left (t-1\right )}\right)
\left \| w_{t} \right \|^{2} \\
= \left \| w_{t-1}+y_{n\left (t-1\right )}x_{n\left (t-1\right )} \right \|^{2} \\
= \left \| w_{t-1} \right \|^{2} + \left \| y_{n\left (t-1\right )}x_{n\left (t-1\right )} \right \|^{2} + 2 y_{n\left (t-1\right )} w_{t-1}^{T} x_{n\left (t-1\right )} \\
\leq \left \| w_{t-1} \right \|^{2} + \left \| y_{n\left (t-1\right )}x_{n\left (t-1\right )} \right \|^{2} \\
\leq \left \| w_{t-1} \right \|^{2} + max_{k} \left \| y_{k\left (t-1\right )}x_{k\left (t-1\right )} \right \|^{2} \\
\leq \left \| w_{0} \right \|^{2} + T*max_{k} \left \| y_{k\left (t-1\right )}x_{k\left (t-1\right )} \right \|^{2}
做道题:
解答:

2.4 Non-Separable Data
上面假设的是训练集D是线性可分的,如果训练集D不是线性可分的,PLA怎么运行?
PLA的优缺点:
如果训练集D不是线性可分的,也就是说存在噪音,PLA就需要变成Pocket。
Pocket算法核心将当前犯错最少的权重向量w放在“口袋”里。
1. 事先规定迭代的次数。
2. 随机地在训练集中抽点试错,如果找到被误分类的点,调整wt+1=wt+yn(t)xn(t)。这算一次迭代。
3. 比较“口袋”中的w和新调整的wt+1在整个训练集中误分率,选出误分率低的权重向量放在“口袋”里。
4. 直到达到事先规定迭代的次数,停止。

做道题:

解答:

总结:
下面几篇文章也是关于林老师《机器学习基石》的上课笔记,交叉着看,可以博取众长。
http://blog.csdn.net/xyd0512/article/details/43484651
https://www.douban.com/note/319669984/
http://www.cnblogs.com/ymingjingr/p/4271761.html
http://www.cnblogs.com/HappyAngel/p/3456762.html
http://my.oschina.net/findbill/blog/205805
疑问:感知机中wf和wt的内积越来越大,但是为什么可以说wt的长度增加非常缓慢,使得wf和wt的内积的增加是两者角度的靠近靠近?





