Coursera 机器学习 第8章(下) Dimensionality Reduction 学习笔记
8 Dimensionality Reduction
8.3 Motivation
8.3.1 Motivation I: Data Compression
第二种无监督问题:维数约简(Dimensionality Reduction)。
通过维数约简可以实现数据压缩(Data Compression),数据压缩可以减少计算机内存使用,加快算法运算速度。
什么是维数约简:降维。若数据库X是属于n维空间的,通过特征提取或者特征选择的方法,将原空间的维数降至m维,要求n远大于m,满足:m维空间的特性能反映原空间数据的特征,这个过程称之为维数约简。
做道题:

C
8.3.2 Motivation II: Visualization
数据降维可以可视化数据,使得数据便于观察。
做道题:

BD
8.4 Principal Component Analysis
8.4.1 Principal Component Analysis Problem Formulation
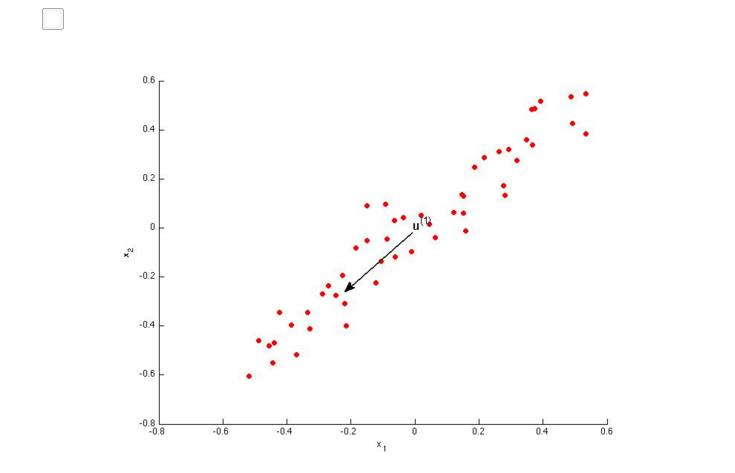
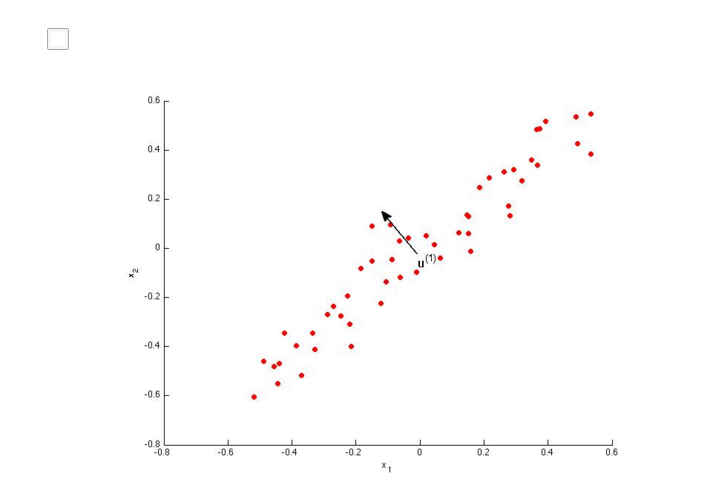
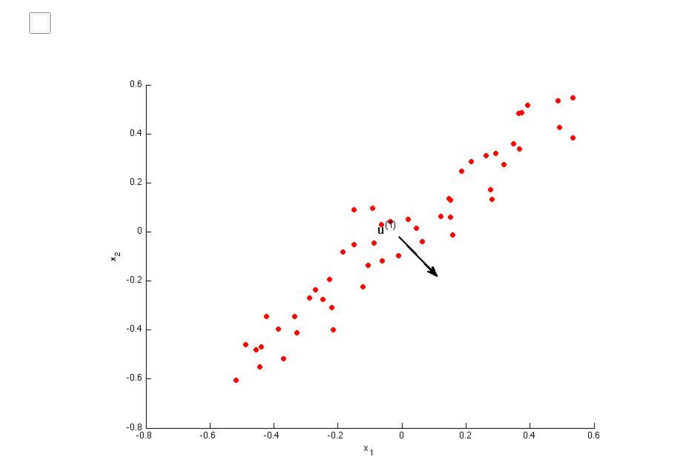
PCA的正式描述:将n维数据投影至由k个正交向量组成的线性空间(k维)并要求最小化投影误差(投影前后的点的距离)(Projection Error)的平方的一种无监督学习算法。
进行PCA之前,先进行均值归一化和特征规范化,使得数据在可比较的范围内。
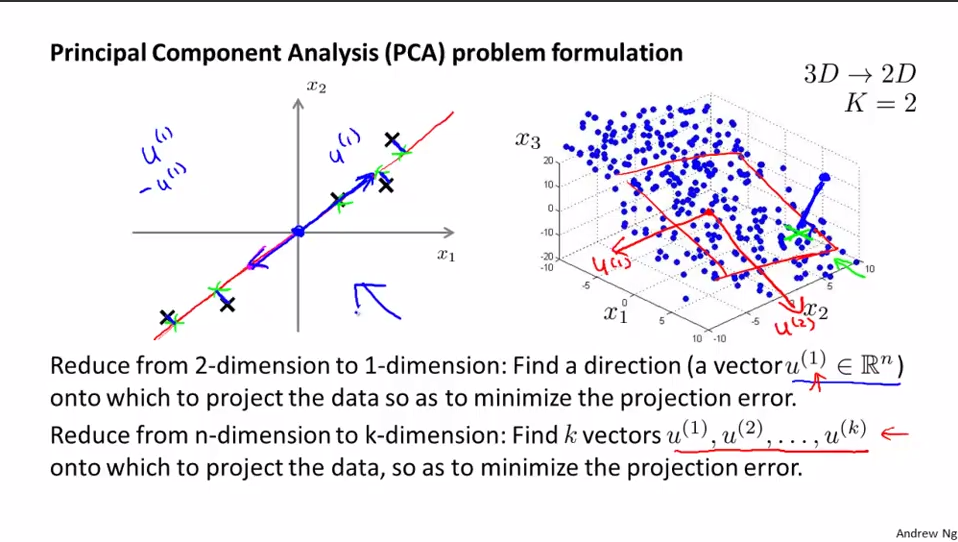
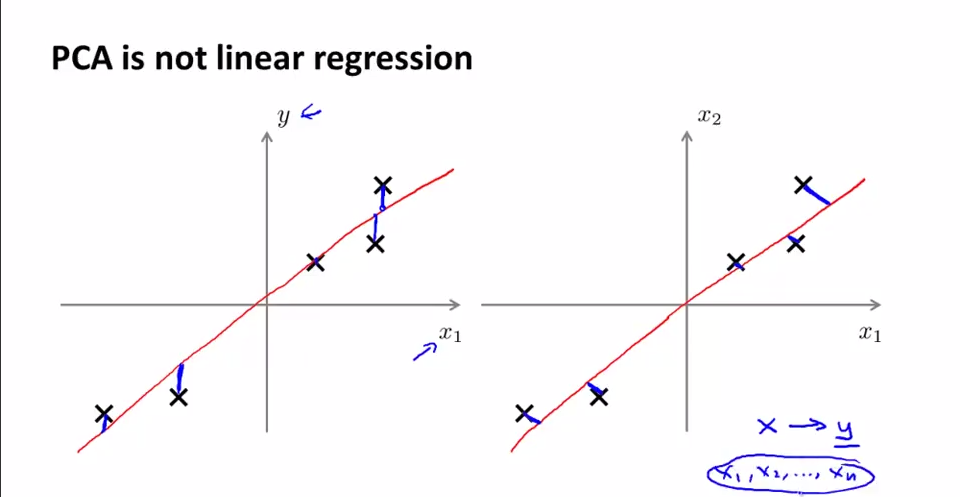
PCA和线性回归之间的关系。PCA不是线性回归。左图是线性回归,右图是PCA。几点不同:
1.最小化的目标不同。PCA衡量的是orthogonal distance, 而linear regression是所有x点对应的真实值y=g(x)与估计值f(x)之间的vertical distance距离。图中蓝线部分为各自最小化目标。
2.PCA中为的是寻找一个surface,将各feature{x1,x2,...,xn}投影到这个surface后使得各点间variance最大(跟y没有关系,是寻找最能够表现这些feature的一个平面);而Linear Regression是给出{x1,x2,...,xn},希望根据x去预测y。
8.4.2 Principal Component Analysis Algorithm
PCA的算法描述,如何将n维数据降至k维:
1.数据预处理。进行特征规范化(feature scaling)和均值归一化(mean normalization)。
均值归一化(mean normalization):对于某一特征j,求j特征下m个样本的均值uj=(Σm Xj(i)/m)/m,Xj(i)表示第i个样本的第j维特征的value。将m个样本的任一个样本i的j特征分量替换为x(i)j-uj。显然这时被替换掉的特征的均值为0。
特征缩放(feature scaling):当特征量的范围跨度很大时使用。x(i)j=(x(i)j-uj)/sj。sj可以是最大值-最小值或者是特征j的标准差。

2. 计算协方差矩阵sigma。对于整个数据集X,sigma=(1/m)*XT*X。X是m*n规模。
3.1 如何寻找这个surface?
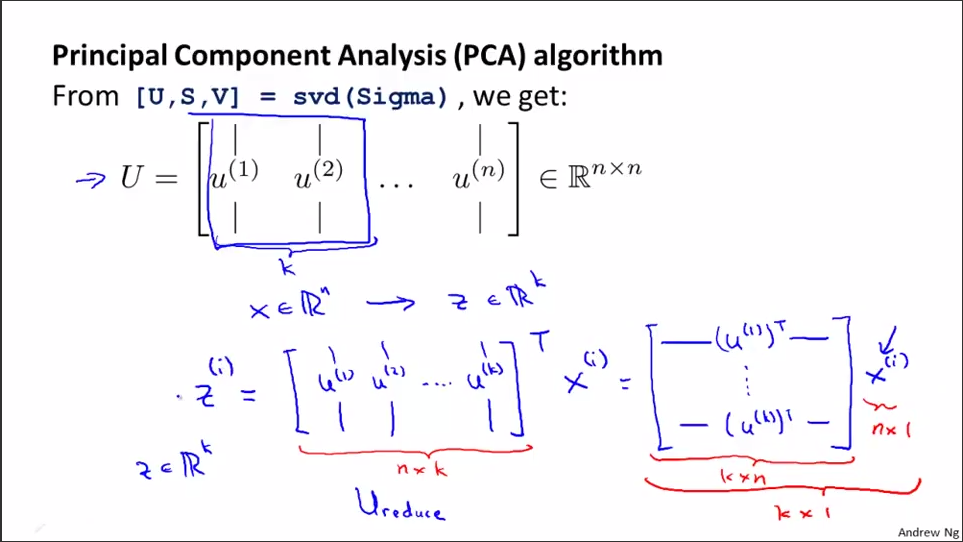
3.1.1 计算协方差矩阵的特征向量(eigenvectors)U。[U,S,V]=svd(sigma)。协方差均值满足对称正定(symmetric positive definite)。sigma和U的规模是n*n。其中,svd表示奇异值分解(singular value decomposition),比eig要稳定。在matlab中有函数[U,S,V] = svd(A) 返回一个与A同大小的对角矩阵S(由A的特征值组成),两个正交矩阵(实数化的酉矩阵)U和V,且满足A= U*S*V'。若A为m×n阵,则U为m×m阵,V为n×n阵。奇异值在S的对角线上,非负且按降序排列。
3.1.2 取U矩阵的前k列,记为Ureduce(n*k维),Ureduce是个正交矩阵。选出这n个特征中最重要的k个,也就是选出特征值最大的k个。
3.2 给定surface,怎样求点到surface投影的value?
3.2.1 Z=X*Ureduce。其中Z是m*k维的;X是m*n维的;Ureduce是n*k维;任一列x(i)没有x0=1一项,是X中的一个实例。
U是n维向量空间的基底,Z是n维数据集X变换至k维空间后对应的k维数据集(维度减少,个数不变)。
这里有个关于PCA算法上述实现数学证明,注意其中维度的变化:http://www.360doc.com/content/13/1124/02/9482_331688889.shtml

也可以看下面的2个图,和上面讲的相同。

做道题:

D
8.5 Applying PCA
8.5.1 Reconstruction from Compressed Representation
将压缩后的低纬度数据还原成原始高维度的方法:重构(Reconstruction)。这里的还原只是近似还原。
具体而言:
1. Z=X*Ureduce,所以只要X*Ureduce*Ureduce-1=Z*Ureduce-1就可以还原了。
2. Ureduce正交矩阵,满足Ureduce-1=UreduceT。
所以映射值Xapprox=X*Ureduce*Ureduce-1==Z*Ureduce-1==Z*UreduceT。这里Z是m*k维;Ureduce是n*k维。
做道题:

ABC
8.5.2 Choosing the Number of Principal Components
如何确定主成分的数量k。
理论上,不断尝试每个k=i(i≤n),计算下式(a):
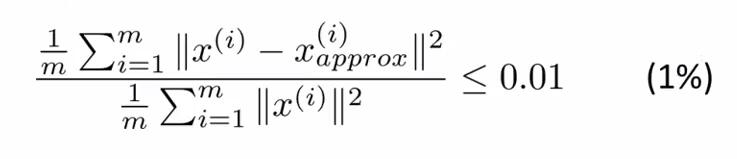
由小到大,取第一个满足(a)式的k的值为主成成分的k。
注意:
1.(a)式的分母是数据的总变差(Total Varuation)。
2.(a)式的分子是x和其映射值之间的平均距离。
3.x(i)approx是还原以后的数据。
4.式子右侧的0.01是可变的,可以取0.05,0.1等,用来衡量保留多少主成成分的指标。取0.01,意思是当前k值下,保留了99%的差异性。也是平方投影误差的测量指标,是衡量是否对原始数据做了一个好的近似的标准。
由于实际中的特征量通常具有高度相关性,所以压缩后保留99%的差异性还是有可能的。
但实际上不需要依次尝试不同的k下的(a)式的值来决定是否采用k。
[U,S,V]=svd(Sigma)中得到的S是一个对角矩阵,这里可以证明(1)和(2)等价(也可以这么理解,Sii表示的是数据从n维映射到k维以后的数据在第i维的方差,也就是映射以后数据在第i维的离散程度。(1)和(2)表示的都是映射以后的数据还保留原数据特征的程度大小,(1)从数据分布的离散程度,(2)从数据的可恢复程度):
(1)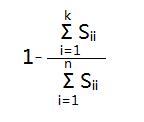
(2)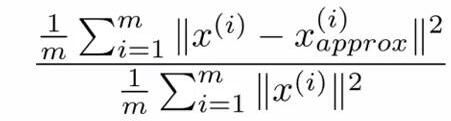
所以只要用(1)代替(2)嵌入到不同k的循环中就可以了。比如原来是求第一个满足(2)≤0.01的k值,那么就可以等价为第一个满足(1)≤0.01的k值。这样就简单很多。

做道题:

C
8.5.3 Advice for Applying PCA
PCA如何提高机器学习算法的速度并提供一些应用PCA的建议。
将PCA用于监督学习的加速。将训练集抽去对应标签y,对无标签的训练集运行PCA,可以得到映射关系。后期可以将这个关系用于交叉验证集和测试集,但不能用交叉验证集和测试集训练这个映射关系。

PCA的应用:数据压缩和可视化数据。

关于PCA的误用:
1.不能使用PCA来避免过拟合。如果要避免过拟合,还是要使用正则化技术。因为PCA实现时,不需要顾及样本的标签y,这意味着PCA丢弃了一些信息。PCA是在对数据标签毫不知情的情况下对数据进行降维。
2.不要盲目使用PCA。对于特定算法,可以先不使用PCA看一下运行效果,只有当算法收敛得非常慢,占用内存非常厉害,也就是x(i)的效果真的不好的时候,再考虑使用PCA。
做道题:

ABD
练习:
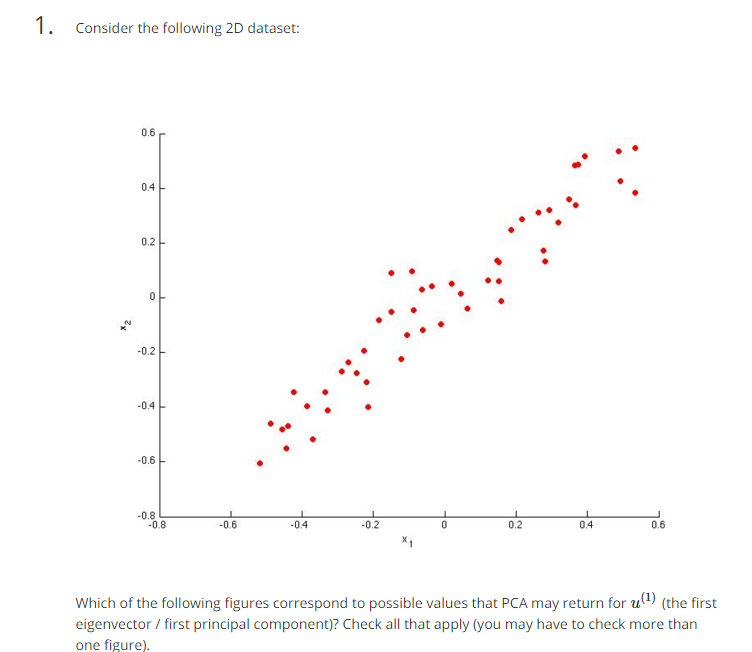
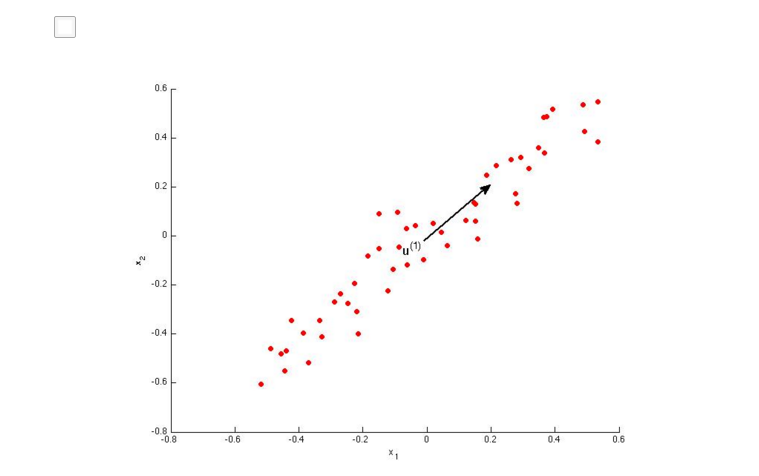
AB

B

C

BD

AB




