KD树

什么是KD树

　　Kd-树是K-dimension tree的缩写，是对数据点在k维空间（如二维(x，y)，三维(x，y，z)，k维(x，y，z..)）中划分的一种数据结构，主要应用于多维空间关键数据的搜索（如：范围搜索和最近邻搜索）。本质上说，Kd-树就是一种平衡二叉树。

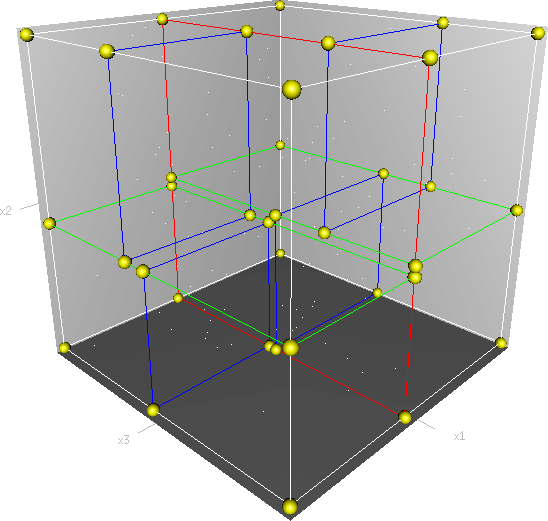
    首先必须搞清楚的是，k-d树是一种空间划分树，说白了，就是把整个空间划分为特定的几个部分，然后在特定空间的部分内进行相关搜索操作。想像一个三维空间，kd树按照一定的划分规则把这个三维空间划分了多个空间，如下图所示：

　　　　　　　　　　　　　　　　　　　　

 

KD树的构建

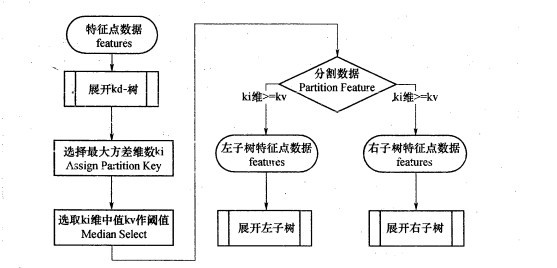
　　伪代码描述：

　　　　　　　　　　　　　　

　　

　　举一个简单直观的实例来介绍k-d树构建算法。假设有6个二维数据点{(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)}，数据点位于二维空间内，如下图所示。为了能有效的找到最近邻，k-d树采用分而治之的思想，即将整个空间划分为几个小部分，首先，粗黑线将空间一分为二，然后在两个子空间中，细黑直线又将整个空间划分为四部分，最后虚黑直线将这四部分进一步划分。

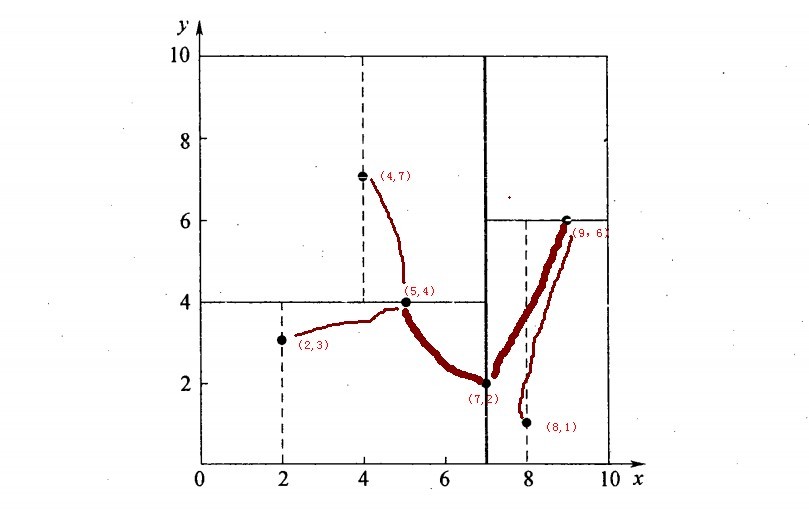
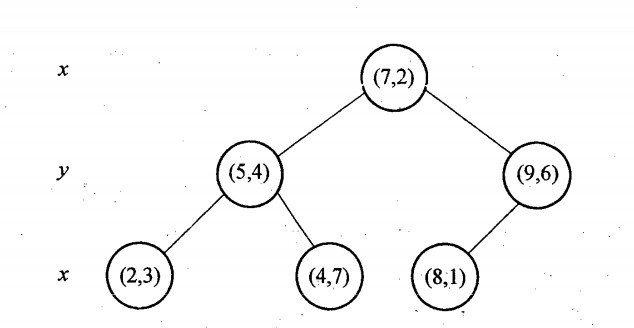
　　6个二维数据点{(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)}构建kd树的具体步骤为：

  1. 确定：split域=x。具体是：6个数据点在x，y维度上的数据方差分别为39，28.63，所以在x轴上方差更大，故split域值为x；
  2. 确定：Node-data = （7,2）。具体是：根据x维上的值将数据排序，6个数据的中值(所谓中值，即中间大小的值)为7，所以Node-data域位数据点（7,2）。这样，该节点的分割超平面就是通过（7,2）并垂直于：split=x轴的直线x=7；
  3. 确定：左子空间和右子空间。具体是：分割超平面x=7将整个空间分为两部分：x<=7的部分为左子空间，包含3个节点={(2,3),(5,4),(4,7)}；另一部分为右子空间，包含2个节点={(9,6)，(8,1)}；
　　如上算法所述，kd树的构建是一个递归过程，我们对左子空间和右子空间内的数据重复根节点的过程就可以得到一级子节点（5,4）和（9,6），同时将空间和数据集进一步细分，如此往复直到空间中只包含一个数据点。
 
　　与此同时，经过对上面所示的空间划分之后，我们可以看出，点(7,2)可以为根结点，从根结点出发的两条红粗斜线指向的(5,4)和(9,6)则为根结点的左右子结点，而(2,3)，(4,7)则为(5,4)的左右孩子(通过两条细红斜线相连)，最后，(8,1)为(9,6)的左孩子(通过细红斜线相连)。如此，便形成了下面这样一棵k-d树：
KD树的最近邻搜索算法

　　k-d树查询算法的伪代码：

 1 算法：k-d树最邻近查找  
 2 输入：Kd，    //k-d tree类型  
 3      target  //查询数据点  
 4 输出：nearest， //最邻近数据点  
 5      dist      //最邻近数据点和查询点间的距离  
 6   
 7 1. If Kd为NULL，则设dist为infinite并返回  
 8 2. //进行二叉查找，生成搜索路径  
 9    Kd_point = &Kd；                   //Kd-point中保存k-d tree根节点地址  
10    nearest = Kd_point -> Node-data；  //初始化最近邻点  
11   
12    while（Kd_point）  
13    　　push（Kd_point）到search_path中； //search_path是一个堆栈结构，存储着搜索路径节点指针  
14   
15       If Dist（nearest，target） > Dist（Kd_point -> Node-data，target）  
16    　　　　nearest  = Kd_point -> Node-data；    //更新最近邻点  
17    　　　　Min_dist = Dist(Kd_point，target）；  //更新最近邻点与查询点间的距离  ***/  
18    　　s = Kd_point -> split；                       //确定待分割的方向  
19   
20    　　If target[s] <= Kd_point -> Node-data[s]     //进行二叉查找  
21    　　　　Kd_point = Kd_point -> left；  
22    　　else  
23    　　　　Kd_point = Kd_point ->right；  
24    End while  
25   
26 3. //回溯查找  
27    while（search_path != NULL）  
28    　　back_point = 从search_path取出一个节点指针；   //从search_path堆栈弹栈  
29    　　s = back_point -> split；                      //确定分割方向  
30   
31    　　If Dist（target[s]，back_point -> Node-data[s]） < Max_dist   //判断还需进入的子空间。这里的Max_dist就是target与当前最近点的距离。  
32    　　　　If target[s] <= back_point -> Node-data[s]  
33    　　　　　　Kd_point = back_point -> right；  //如果target位于左子空间，就应进入右子空间  
34    　　　　else  
35    　　　　　　Kd_point = back_point -> left;    //如果target位于右子空间，就应进入左子空间  
36    　　　　将Kd_point压入search_path堆栈；  
37   
38    　　If Dist（nearest，target） > Dist（Kd_Point -> Node-data，target）  
39    　　　　nearest  = Kd_point -> Node-data；                 //更新最近邻点  
40    　　　　Min_dist = Dist（Kd_point -> Node-data,target）；  //更新最近邻点与查询点间的距离的  
41    End while

 

 

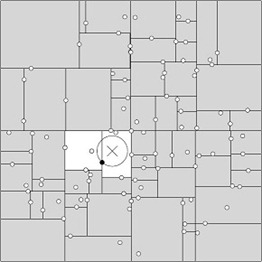
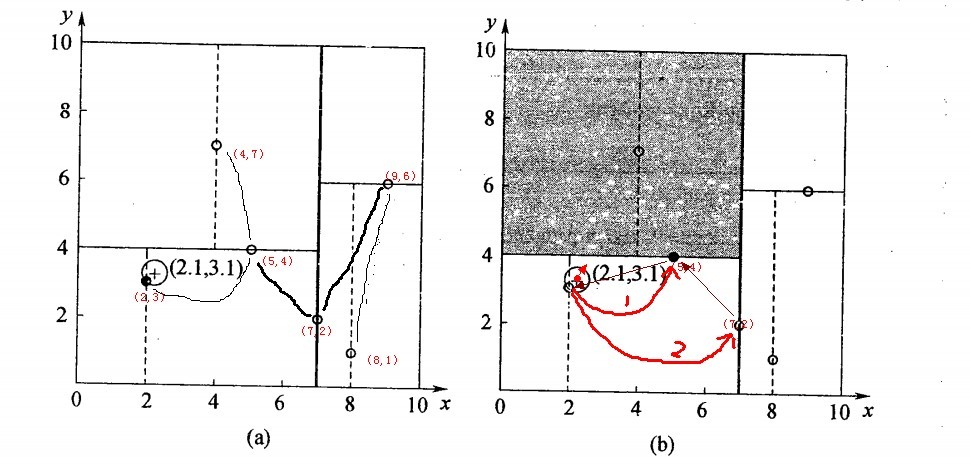
举例：查询点（2.1,3.1）

　　星号表示要查询的点（2.1,3.1）。通过二叉搜索，顺着搜索路径很快就能找到最邻近的近似点，也就是叶子节点（2,3）。而找到的叶子节点并不一定就是最邻近的，最邻近肯定距离查询点更近，应该位于以查询点为圆心且通过叶子节点的圆域内。为了找到真正的最近邻，还需要进行相关的‘回溯'操作。也就是说，算法首先沿搜索路径反向查找是否有距离查询点更近的数据点。

    以查询（2.1,3.1）为例：

  1. 二叉树搜索：先从（7,2）点开始进行二叉查找，然后到达（5,4），最后到达（2,3），此时搜索路径中的节点为<(7,2)，(5,4)，(2,3)>，首先以（2,3）作为当前最近邻点，计算其到查询点（2.1,3.1）的距离为0.1414，
  2. 回溯查找：在得到（2,3）为查询点的最近点之后，回溯到其父节点（5,4），并判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。以（2.1,3.1）为圆心，以0.1414为半径画圆，如下图所示。发现该圆并不和超平面y = 4交割，因此不用进入（5,4）节点右子空间中(图中灰色区域)去搜索；
  3. 最后，再回溯到（7,2），以（2.1,3.1）为圆心，以0.1414为半径的圆更不会与x = 7超平面交割，因此不用进入（7,2）右子空间进行查找。至此，搜索路径中的节点已经全部回溯完，结束整个搜索，返回最近邻点（2,3），最近距离为0.1414。

 

 

 

 

 

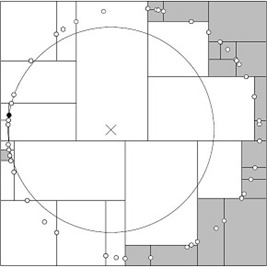
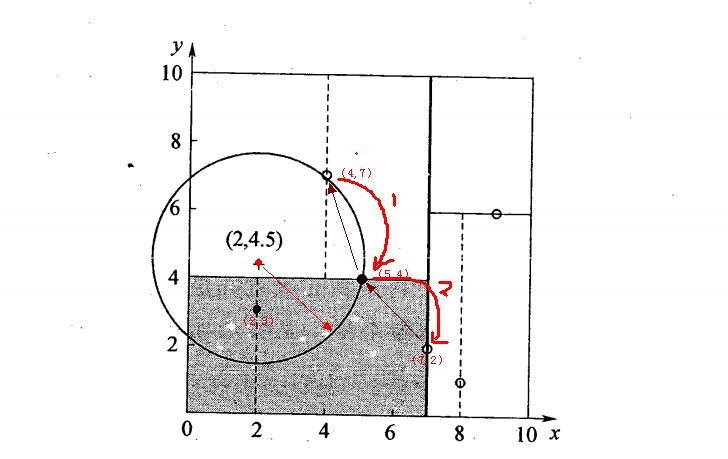
举例：查询点（2，4.5）

    一个复杂点了例子如查找点为（2，4.5），具体步骤依次如下：

  1. 同样先进行二叉查找，先从（7,2）查找到（5,4）节点，在进行查找时是由y = 4为分割超平面的，由于查找点为y值为4.5，因此进入右子空间查找到（4,7），形成搜索路径<(7,2)，(5,4)，(4,7)>，但（4,7）与目标查找点的距离为3.202，而（5,4）与查找点之间的距离为3.041，所以（5,4）为查询点的最近点；
  2. 以（2，4.5）为圆心，以3.041为半径作圆，如下图所示。可见该圆和y = 4超平面交割，所以需要进入（5,4）左子空间进行查找，也就是将（2,3）节点加入搜索路径中得<(7,2)，(2,3)>；于是接着搜索至（2,3）叶子节点，（2,3）距离（2,4.5）比（5,4）要近，所以最近邻点更新为（2，3），最近距离更新为1.5；
  3. 回溯查找至（5,4），直到最后回溯到根结点（7,2）的时候，以（2,4.5）为圆心1.5为半径作圆，并不和x = 7分割超平面交割，如下图所示。至此，搜索路径回溯完，返回最近邻点（2,3），最近距离1.5。

　　上述两次实例表明，当查询点的邻域与分割超平面两侧空间交割时，需要查找另一侧子空间，导致检索过程复杂，效率下降。

 

    一般来讲，最临近搜索只需要检测几个叶子结点即可，如下图所示：　　
    但是，如果当实例点的分布比较糟糕时，几乎要遍历所有的结点，如下所示：
 
　　研究表明N个节点的K维k-d树搜索过程时间复杂度为：tworst=O（kN1-1/k）。
　　同时，以上为了介绍方便，讨论的是二维或三维情形。但在实际的应用中，如SIFT特征矢量128维，SURF特征矢量64维，维度都比较大，直接利用k-d树快速检索（维数不超过20）的性能急剧下降，几乎接近贪婪线性扫描。假设数据集的维数为D，一般来说要求数据的规模N满足N»2D，才能达到高效的搜索。所以这就引出了一系列对k-d树算法的改进：BBF算法，和一系列M树、VP树、MVP树等高维空间索引树。
posted @ 2015-11-07 23:12  Deribs4  阅读(6818)  评论(1)  编辑  收藏  举报