决策树

什么是决策树

　　决策树，一种分类器，大多是用来分类的。

　　对于分类问题，选择分类属性的标准是信息增益最大，涉及到熵这个概念。而在做回归树的时候，选择变量的标准我们用最小均方误差（MSE）。

 

决策树算法的具体描述：

1. 开始，所有记录看作一个节点

2. 遍历每个变量的每一种分割方式，找到最好的分割点

3. 分割成几个节点N_1..Nn

4. 对N₁和N₂分别继续执行2-3步，直到每个节点足够“纯”为止

 　　如果一个分割点可以将当前的所有节点分为几类，使得每一类都很“纯”，也就是同一类的记录较多，那么就是一个好分割点。构建决策树采用贪心算法，只考虑当前纯度差最大的情况作为分割点。

 

停止条件

　　决策树的构建过程是一个递归的过程，所以需要确定停止条件，否则过程将不会结束。一种最直观的方式是当每个子节点只有一种类型的记录时停止，但是这样往往会使得树的节点过多，导致过拟合问题（Overfitting）。另一种可行的方法是当前节点中的记录数低于一个最小的阀值，那么就停止分割，将max(P(i))对应的分类作为当前叶节点的分类。

 

如何找到最好的分割点：http://www.cnblogs.com/fengfenggirl/p/classsify_decision_tree.html

　　属性选择方法总是选择最好的属性作为分裂属性，即让每个分支的记录的类别尽可能纯。它将所有属性列表的属性进行按某个标准排序，从而选出最好的属性。属性选择方法很多，这里介绍三个常用的方法：信息增益（Information gain）、增益比率（gain ratio）、基尼指数（Gini index）。

 

• 信息增益（Information gain）

选择标准：以属性R分裂前后的信息增益比其他属性最大　　

　　

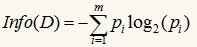
　　其中的m表示数据集D中类别C的个数，Pi表示D中任意一个记录属于Ci的概率，计算时Pi=(D中属于Ci类的集合的记录个数/|D|)。Info(D)表示将数据集D不同的类分开需要的信息量。Info实际上就是信息论中的熵Entropy，熵表示的是不确定度的度量，如果某个数据集的类别的不确定程度越高，则其熵就越大。

　　假设我们选择属性R作为分裂属性，数据集D中，R有k个不同的取值{V1,V2,...,Vk}，于是可将D根据R的值分成k组{D1,D2,...,Dk}，按R进行分裂后，将数据集D不同的类分开还需要的信息量为： 

　　

　　信息增益的定义为分裂前后，两个信息量只差：

　　

　　信息增益Gain(R)表示属性R给分类带来的信息量，寻找Gain最大的属性，就能使分类尽可能的纯，即最可能的把不同的类分开。不过发现对所有的属性Info(D)都是一样的，所以求最大的Gain可以转化为求最小的InfoR(D)。这里引入Info(D)只是为了说明背后的原理，方便理解，实现时不需要计算Info(D)。

　　举一个例子，数据集D如下：

记录ID	年龄	输入层次	学生	信用等级	是否购买电脑
1	青少年	高	否	一般	否
2	青少年	高	否	良好	否
3	中年	高	否	一般	是
4	老年	中	否	一般	是
5	老年	低	是	一般	是
6	老年	低	是	良好	否
7	中年	低	是	良好	是
8	青少年	中	否	一般	否
9	青少年	低	是	一般	是
10	老年	中	是	一般	是
11	青少年	中	是	良好	是
12	中年	中	否	良好	是
13	中年	高	是	一般	是
14	老年	中	否	良好	否

　　这个数据集是根据一个人的年龄、收入、是否学生以及信用等级来确定他是否会购买电脑，即最后一列“是否购买电脑”是类标。现在我们用信息增益选出最最佳的分类属性，计算按年龄分裂后的信息量：

　　

　　整个式子由三项累加而成，第一项为青少年，14条记录中有5条为青少年，其中2（占2/5）条购买电脑，3（占3/5）条不购买电脑。第二项为中年，第三项为老年。类似的，有：

　　

　　

　　可以得出Info年龄(D)最小，即以年龄分裂后，分得的结果中类标最纯，此时已年龄作为根结点的测试属性，根据青少年、中年、老年分为三个分支：

　　注意，年龄这个属性用过后，之后的操作就不需要年龄了，即把年龄从attributeList中删掉。往后就按照同样的方法，构建D1,D2,D3对应的决策子树。ID3算法使用的就是基于信息增益的选择属性方法。

 

• 增益比率（gain ratio）

　　信息增益选择方法有一个很大的缺陷，它总是会倾向于选择属性值多的属性，这里可以这样解释：信息增益的目的是使选择以后的各个集合的熵和最小（不确定性最小），按选择属性值多的属性分类，可以达到这个目的。

　　如果我们在上面的数据记录中加一个姓名属性，假设14条记录中的每个人姓名不同，那么信息增益就会选择姓名作为最佳属性，因为按姓名分裂后，每个组只包含一条记录，而每个记录只属于一类（要么购买电脑要么不购买），因此纯度最高，以姓名作为测试分裂的结点下面有14个分支。于是引入一个分裂信息：

　　

　　增益比率定义为信息增益与分裂信息的比率：

　　

 

　　我们找GainRatio最大的属性作为最佳分裂属性。如果一个属性的取值很多，那么SplitInfoR(D)会大，从而使GainRatio(R)变小。不过增益比率也有缺点，SplitInfo(D)可能取0，此时没有计算意义；且当SplitInfo(D)趋向于0时，GainRatio(R)的值变得不可信，改进的措施就是在分母加一个平滑，这里加一个所有分裂信息的平均值：

　　

 

• 基尼指数（Gini index）

　　基尼指数是另外一种数据的不纯度的度量方法，其定义如下：

　　　　

　　其中的m仍然表示数据集D中类别C的个数，Pi表示D中任意一个记录属于Ci的概率，计算时Pi=(D中属于Ci类的集合的记录个数/|D|)。如果所有的记录都属于同一个类中，则P1=1，Gini(D)=0，此时不纯度最低。在CART(Classification and Regression Tree)算法中利用基尼指数构造二叉决策树，对每个属性都会枚举其属性的非空真子集，以属性R分裂后的基尼系数为：

　　

　　D1为D的一个非空真子集，D2为D1在D的补集，即D1+D2=D，对于属性R来说，有多个真子集，即GiniR(D)有多个值，但我们选取最小的那么值作为R的基尼指数。　　最后：

　　

　　我们选Gini(R)增量最大的属性作为最佳分裂属性。

 

　　基尼指数和信息增益的实现形式上差不多，最后都是选增益最大的，也就是公式中被减部分最小。增益比率是为了克服信息增益的倾向于选择属性值多的属性的缺陷。

 

停止条件：

 

 

 

过渡拟合的问题及解决： 

 

 

 

 

如何找到最好的分割点：http://www.cnblogs.com/fengfenggirl/p/classsify_decision_tree.html

CART: 分类与回归树：http://www.dataguru.cn/article-4720-1.html

ID3算法、C4.5算法等算法的实现：http://blog.csdn.net/v_july_v/article/details/7577684

决策树过渡拟合解决方法：http://www.cnblogs.com/bourneli/archive/2013/03/15/2961568.html

决策树的实现：http://blog.csdn.net/hewei0241/article/details/8280490