数独求解——面向对象解决算法问题(一)
最近遇到一个算法题,名字叫做数独求解,问题描述如下:
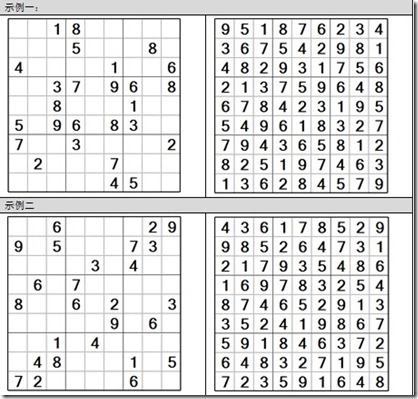
在9*9的方阵中,包含了81个小格子(九行九列),其中又再分成九个小正方形(称为宫),每宫有九小格。游戏刚开始时,盘面上有些小格已经填了数字(称为初盘),游戏者要在空白的小格中填入1到9的数字,使得最后每行、每列、每宫中都包含1到9,但不允许出现重复的数字,而且每一个游戏都只有一个唯一的解答(称为终盘)。如下给出两个示例:
解决这样的算法问题,面向过程语言通常是最佳方法,因为第一:出题的人不希望看到你爱面向对象语言中封装的一些特性,第二,面向对象的效率相对较低。
但是另一方面,面向对象的利用性、易读性、易维护性以及其大量的对象特性和内库,为我们解决算法问题提供了良好的解决方法,费话少说,下面讲一下我的解题步骤。
第一步:抽象
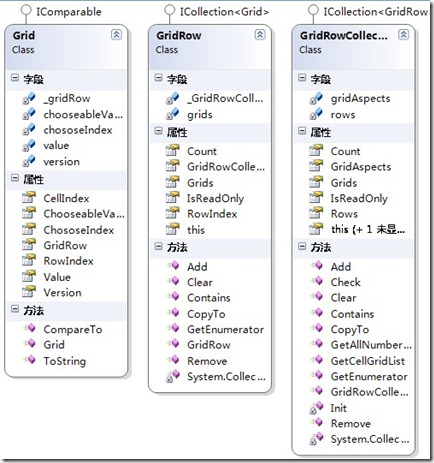
在这里,我共抽象出三个类,分别是Grid(每个单元格)、GridRow(每一行)、GridRowCollection(整个棋盘),具体如下:
1. Grid类:
本题中的最小单元,代表一个单元格,且必须属于一行。实现了ICompare接口,重写了CopareTo()方法,用以比较不两只单元格的大小,其各个成员的解释如下:
RowInde:单元格所在行的坐标
CellIndex:单元格所在列的坐标
GridRow:只读属性,单元格所在的行对象
Value:单元格上的值,如1~9
Version:单元格上的数字被修改的次数
ChooseableValues:单元值上可选的值的数组,如示例一中,单元格[3,0]可选的数字为{1,2}
ChooseIndex:当前所行的值在ChooseableValues中的坐标,以来做回溯用
2. GridRow类:
实现了ICollection<Grid>接口,用以实现该行上单元格的添加、删除等操作。
Count:该行上单元格的数目
Grids:该行上单元格组成的数组
GridRowCollection:该行所属的棋盘对象
RowIndex:该行的索引
this[]:索引,返回该行指定列上的单元格
3. GridRowColllection类:
实现了ICollection<GridRow>接口,用以实现该行上单元格的添加、删除等操作。
Count:返回该棋盘上所有的格子数组
GridAspects:维数,即行数或列数,本题中为9
Rows:返回当前棋盘的所有行数组
this[]:返回指定行
this[ , ]:返回指定位置的单元格
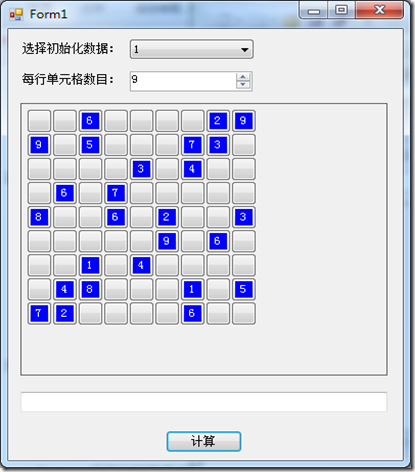
剩下的就是前台了,界面如下:
其中下拉列表用来选择不同的初始化情况,即不两只的棋盘。numberupdown控件用来设置棋盘维数,Panel中的各个按钮就来示棋盘中的格子了,其中蓝色的来示初始化的数据,不允许被修改。
看代码:
下拉列表中的事件:
private void comboBox1_SelectedIndexChanged(object sender, EventArgs e)
{
// 棋盘维数
int gridAspects = Convert.ToInt32(this.numericUpDown1.Value);//初始化棋盘对象
gridCollection = new GridRowCollection(gridAspects);
int i = Convert.ToInt32(this.comboBox1.Text);
//加载棋盘中的初始化数据
switch (i)
{
case 1:
Init1();
break;
case 2:
Init2();
break;
case 3:
Init3();
break;
case 4:
Init4();
break;
case 5:
Init5();
break;
default:
break;
}
foreach (Grid g in gridCollection.Grids)
{
if (g.Value != 0)
{
g.Version = -1; //表示为不可修改的单元格
}
}// 来用加载按钮
FirstLoadGrids();
}其中函数结尾处的FirstLoadGrids()表示第一次加载(初始化)时,加载各个按钮,代码如下:
/// <summary>
/// 第一次加载每行上的格子
/// </summary>
private void FirstLoadGrids()
{
this.panel1.Controls.Clear();
foreach (Grid g in this.gridCollection.Grids)
{
Button btn = new Button();
btn.Name = string.Format("btn_{0}_{1}", g.RowIndex, g.CellIndex);
btn.TabStop = false;
if (g.Value != 0)
{
btn.Text = g.Value.ToString();
}
btn.Width = 25;
btn.Height = 25;
if (g.Version == -1 && g.Value != 0)
{
btn.BackColor = Color.Blue;
btn.ForeColor = Color.White;
}
int x = 0 + btn.Width * g.CellIndex + 5;
int y = 0 + btn.Height * g.RowIndex + 5;
btn.Location = new Point(x, y);
this.panel1.Controls.Add(btn);
}
}
好了,接下来讲核心部分,即算法的实现:
Stack<Grid> s = new Stack<Grid>();
/// <summary>
/// 递归、回溯求解
/// </summary>
private void LoadGrids()
{
Grid g;
try
{
g = this.gridCollection.Grids.First<Grid>(gitem => gitem.Value == 0);
}
catch (InvalidOperationException) { return; }
if (g == null)
{
return;
}
int minCount = this.gridCollection.GridAspects;
foreach (Grid gItem in this.gridCollection.Grids)
{
if (gItem.Version == -1 || gItem.Value != 0)
{
continue;
}
gItem.ChooseableValues = this.GetChooseableValues(gItem);
if (gItem.ChooseableValues.Count < minCount)
{
minCount = gItem.ChooseableValues.Count;
g = gItem;
}
}
if (g.ChooseableValues.Count > 0)
{
g.Value = g.ChooseableValues[g.ChososeIndex];
s.Push(g);
string btnName = string.Format("btn_{0}_{1}", g.RowIndex, g.CellIndex);
this.panel1.Controls[btnName].Text = g.Value.ToString();
}
else
{
if (s == null || s.Count == 0)
{
return;
}
Grid preGrid = s.Peek();
while ((preGrid.ChooseableValues.Count <= 1) || (preGrid.ChososeIndex == preGrid.ChooseableValues.Count - 1))
{
preGrid.ChososeIndex = 0;
preGrid.Value = 0;
preGrid = s.Pop();
}
preGrid.Value = 0;
preGrid.Version = preGrid.Version - 2;
preGrid.ChososeIndex++;
}
LoadGrids();
}
讲解:
第一步:找出所有格子中未被赋值的单元格
第二步:从这些单元格中,根据其行、列上其他的已经确定的值,判断每个单元格上可选值的数目,选取可选数最小的一个单元格。如示例一中,单元格【3,0】,可选值只有{1,2}两个值,其他的所有单元格的可选值均大于(或等于2),所以我们第一步就选【3,0】
第三步:从其可选的值中挑选一个,并值给该单元格。并将该单元格加入一个全局的栈中,记录起来
第四步:递归调用第二步和第三步,直到最后会有两种走向:
1.如果所有的单元格中都有数字时,问题求解出来了(当然这这情况很少发生);
2.计算到某个单元格时,发现其无可选值了,那么就说明前面所选的单元格中,至少有一个是选错了的。如是,后退一步(我们称为回溯),到上一个计算的单元上(该单元格已经入库)。
2.1 从栈中将当元格出栈,从其可选的数字中,选取其他的可选的值(即ChooseIndex++),然后递归到第二步。
2.2 如果栈中的值限完,或者所有的单元格均已填满,则表示算法完成。
由于时间关系,现在必须去睡觉了,接下来的我可以明天再写。具体要写的为:
1.这样面向对象的写法有什么好处?有什么缺点呢?
2.系统中存在很多严重的设计问题,你是否发现了?
3.本题中,用栈来进行记录操作,那么是否可以用队列呢?哪个更好?为什么?
4.这个题还有很多其他的算法,希望大家一起来讨论。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号