论文笔记11 - "Linear Convergence in Federated Learning: Tackling Client Heterogeneity and Sparse Gradients"
内容总结全在摘要里，下面是一些证明
Deterministic
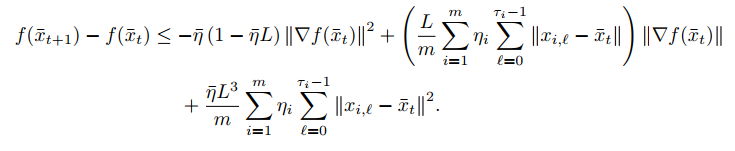
上面这个式子只要求了\(f\)函数\(L\)-smooth。
对于
\[\Vert x_{i,\ell}-\bar{x}_t\Vert^2
\]
可以看作对多步gradient的norm。在convex和strongly convex的条件下可以得到
\[\Vert x_{i, \ell} - \bar{x}_t\Vert \leq \eta\ell\Vert \nabla f(x_t)\Vert^2
\]
这里引入的SVRG优势就凸显出来了，可以分离出\(\nabla f(x_t)\)而不是\(\nabla f_i(x_{i,\ell-1})\)。
Strongly convex
代入可以得到
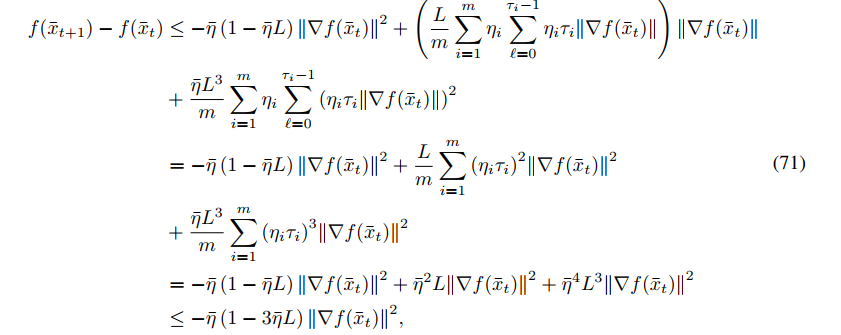
这里确定\(f(\bar{x}_{t+1})\)和\(f(\bar{x}_t)\)之间的下降上界，然后根据strongly convex的性质，
\[\Vert \nabla f(\bar{x}_t)\Vert^2 \geq 2\mu (f(\bar x_t) - f(x^*))
\]
得到
\[f(\bar x_{t+1}) - f(x^*)\leq(1- \frac{1}{6\kappa})(f(\bar x_{t}) - f(x^*))
\]
convex
对于convex场景，我们有
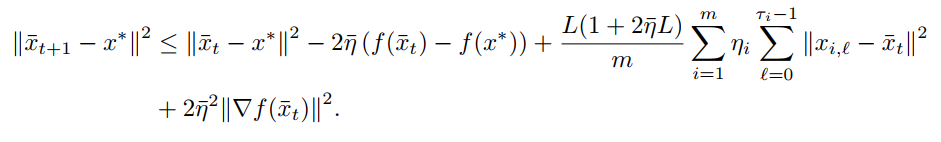
代入\(\Vert x_{t, \ell} -\bar x_t\Vert^2\)
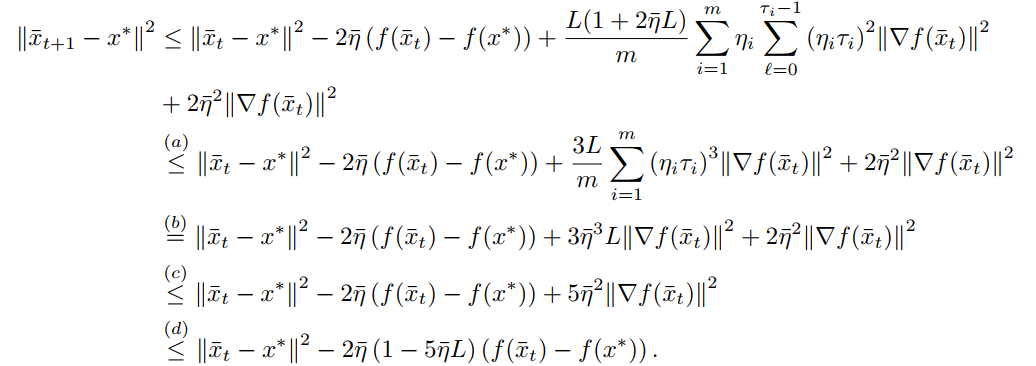
Nonconvex
对于nonconvex场景，需要重新确定\(\Vert x_{i, \ell} - \bar x_{t}\Vert^2\)
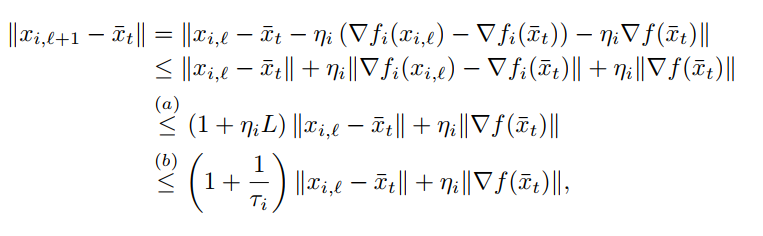
代入即可得
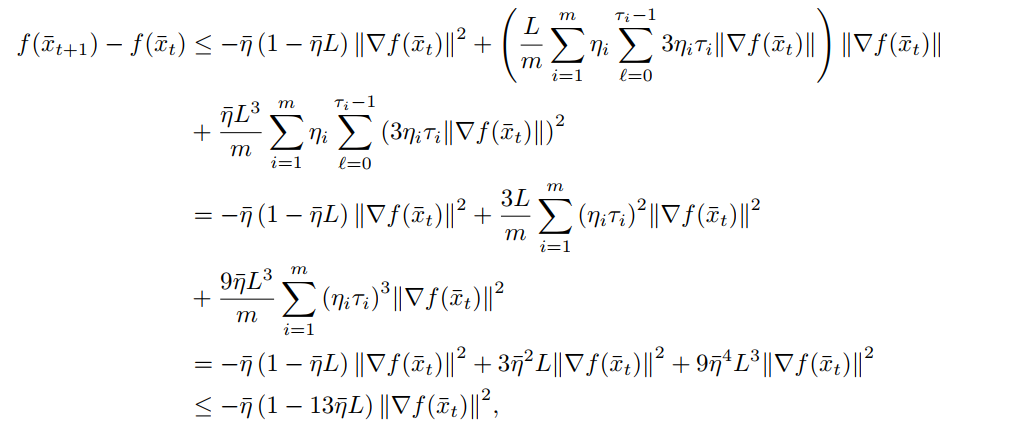
Stochastic
相对于随机的场景，要多出因为随机采样而导致的误差项。
Strongly-convex
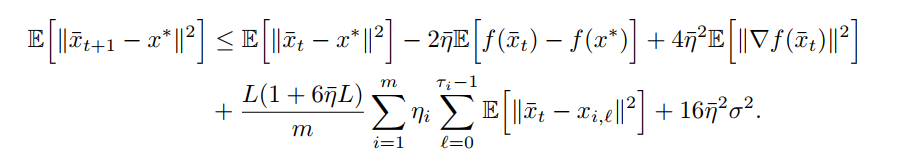
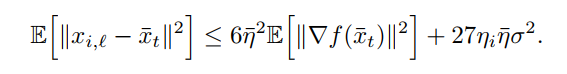
summary
- 个人认为，他讨论的infrequence communication没啥意义，因为他的学习率是关于H的函数，H变大学习率就减小，它们俩的乘积是固定的。
- 证明过程还是很清晰简洁的
